コーシー分布のシミュレーション

コーシー分布 をシミュレーションで確認します。

始めに 期待値が定義されない事から中心極限定理が成立しない ことをシミュレーションで確認します。

以降、共通して有意水準は 5% とします。

一様分布、ガンマ分布 そして コーシー分布 のサンプルを作成します。

なお、関数 rcauchy 及び qcauchy の引数 scale は半値半幅です。

set.seed(20240531)
n <- 10^6
v_unif <- runif(n = n, min = -10^3, max = 10^3)
v_gamma <- rgamma(n = n, shape = 2, scale = 1)
v_cauchy <- rcauchy(n = n, location = 0, scale = 1)

以下は、10万個のサンプルから1組100個、計5000組をランダムに抽出してそれぞれの組の平均値を求め、それら5000個の平均値のヒストグラムを描き、正規性を検定する関数 です。

library(dplyr)
library(ggplot2)
library(ggpubr)
fun_test <- function(v) {
  result <- seq(5000) %>%
    sapply(FUN = function(x) sample(x = v, size = 100, replace = T) %>% mean()) %>%
    data.frame() %>%
    {
      colnames(.)[1] <- "x"
      .
    }
  g <- ggplot(result, aes(x = x)) +
    geom_histogram(aes(y = after_stat(density)), colour = 1, fill = "white") +
    geom_density()
  normality <- ks.test(x = result$x, y = "pnorm", mean = mean(result$x), sd = sd(result$x))
  return(list(g = g, normality = normality))
}

一様分布のシミュレーションを確認します。

Uniform{stats}を利用した連続一様分布の確率密度関数
...
www.saecanet.com
2024.05.25
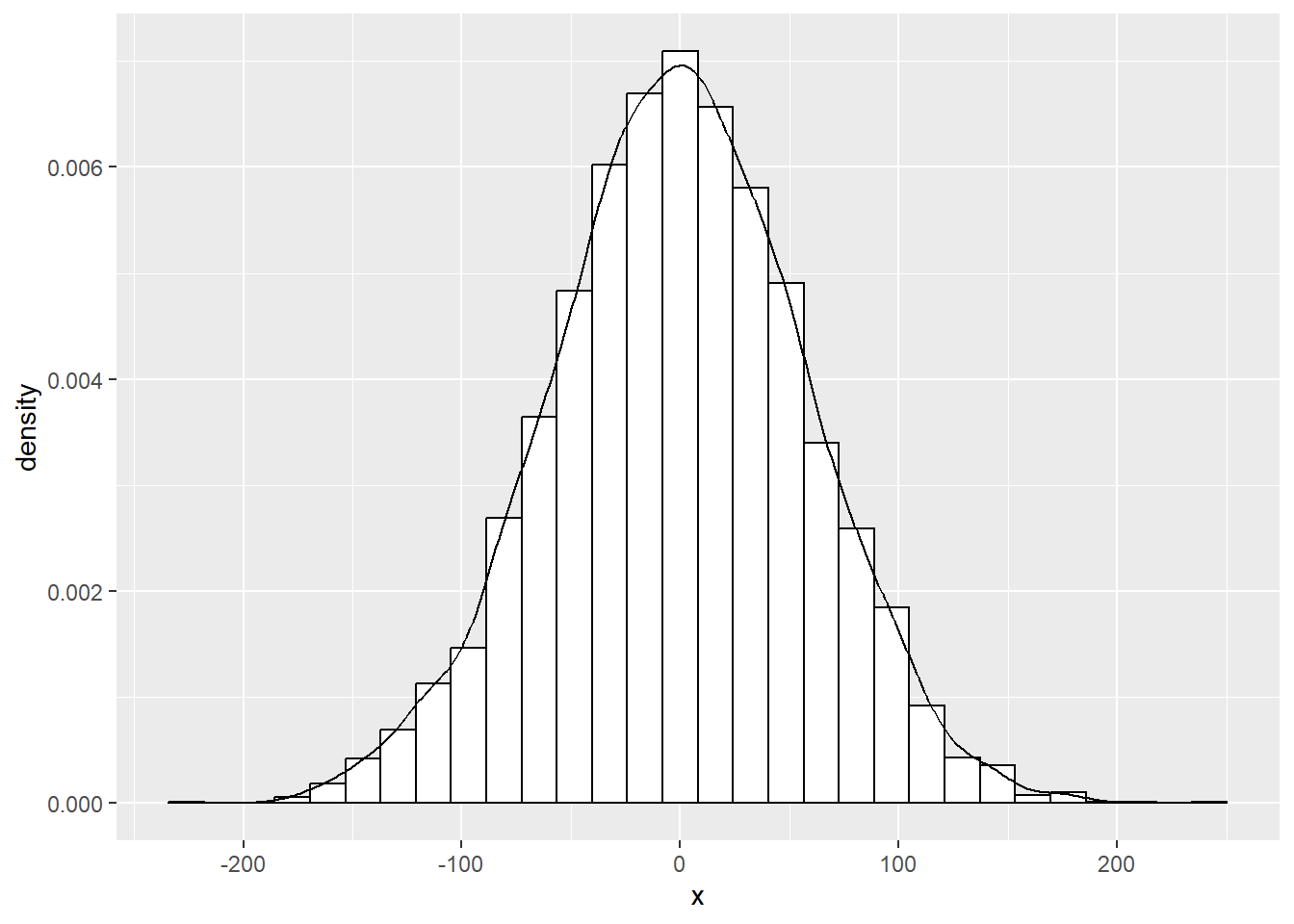
fun_test(v = v_unif)$g
fun_test(v = v_unif)$normality

    Asymptotic one-sample Kolmogorov-Smirnov test

data:  result$x
D = 0.0081361, p-value = 0.8952
alternative hypothesis: two-sided
Figure 1

コルモゴロフ・スミルノフ検定の結果、正規性は棄却されません。

続いて、ガンマ分布です。

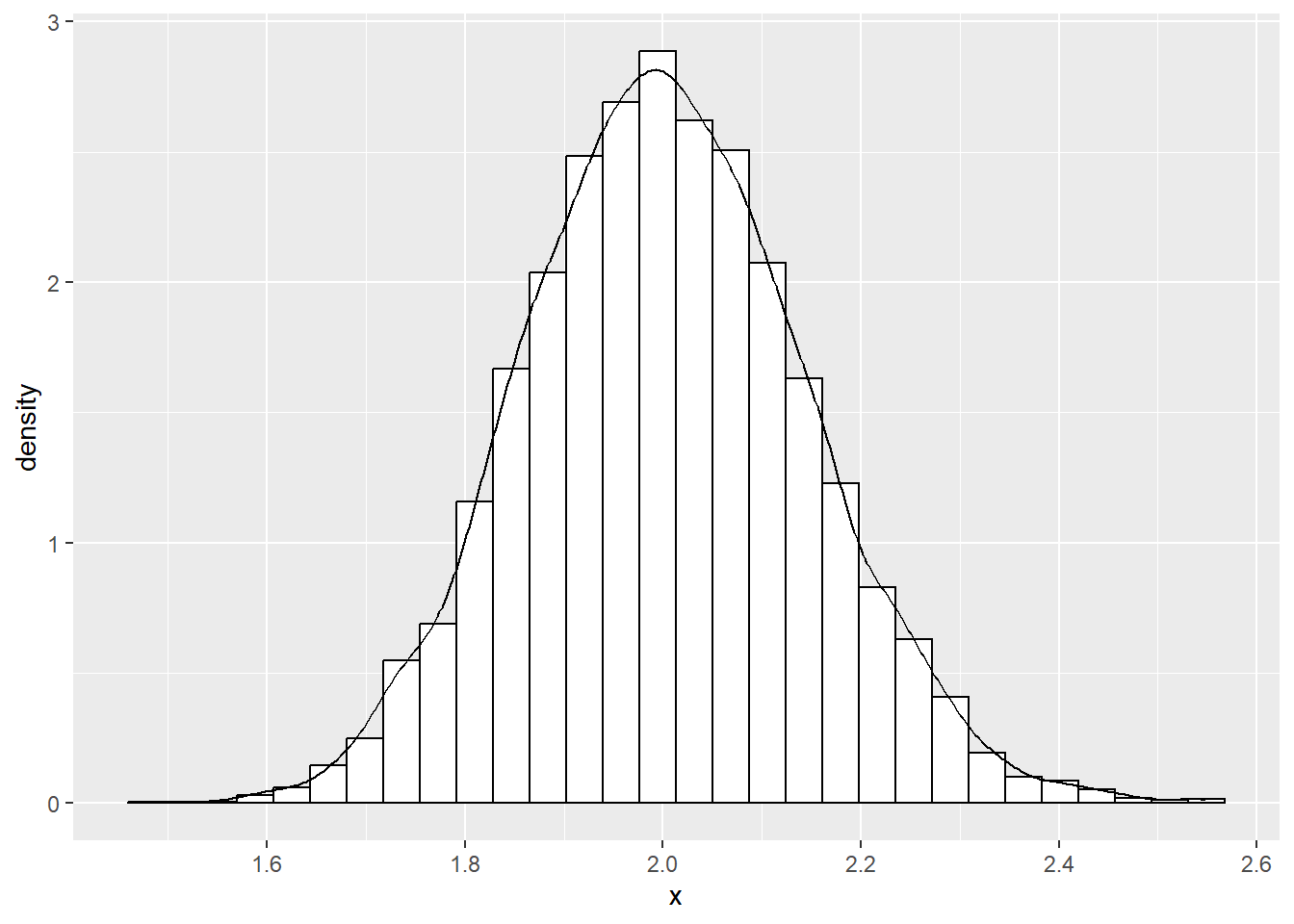
fun_test(v = v_gamma)$g
fun_test(v = v_gamma)$normality

    Asymptotic one-sample Kolmogorov-Smirnov test

data:  result$x
D = 0.013144, p-value = 0.3534
alternative hypothesis: two-sided
Figure 2

こちらも正規性は棄却されません。

最後にコーシー分布です。

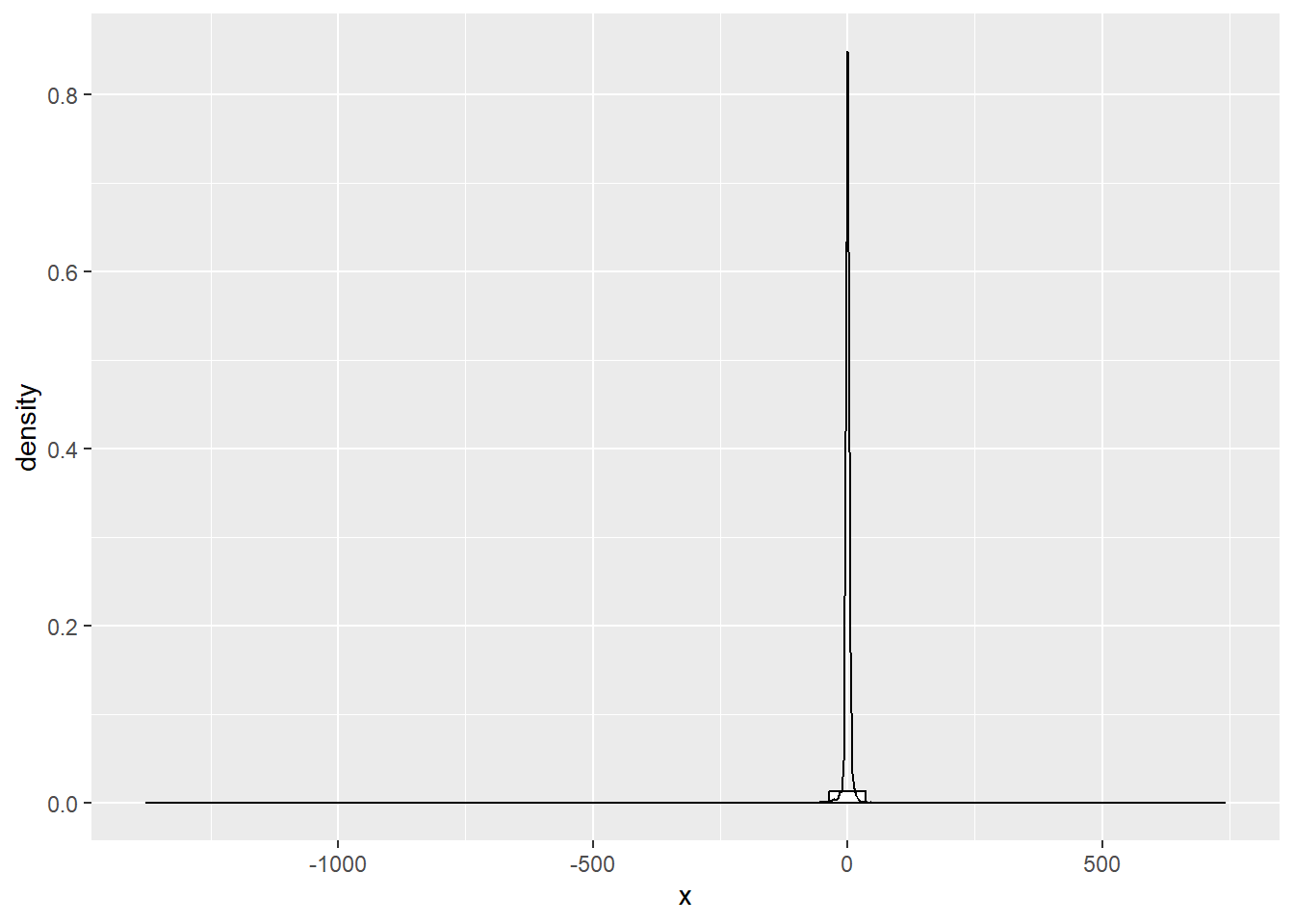
fun_test(v = v_cauchy)$g
fun_test(v = v_cauchy)$normality

    Asymptotic one-sample Kolmogorov-Smirnov test

data:  result$x
D = 0.39983, p-value < 2.2e-16
alternative hypothesis: two-sided
Figure 3

正規性が棄却されます。

正規分布と比較した場合の 裾の厚さ を確認します。

prob <- seq(0.9, 0.99, 0.005)
q <- prob %>% sapply(FUN = function(x) qnorm(p = x, mean = 0, sd = 1, lower.tail = T))
data.frame(normal = prob, cauchy = pcauchy(q = q, location = 0, scale = 1, lower.tail = T))
   normal    cauchy
1   0.900 0.7890830
2   0.905 0.7925311
3   0.910 0.7960147
4   0.915 0.7995396
5   0.920 0.8031125
6   0.925 0.8067413
7   0.930 0.8104351
8   0.935 0.8142052
9   0.940 0.8180648
10  0.945 0.8220306
11  0.950 0.8261234
12  0.955 0.8303696
13  0.960 0.8348044
14  0.965 0.8394752
15  0.970 0.8444492
16  0.975 0.8498262
17  0.980 0.8557660
18  0.985 0.8625515
19  0.990 0.8707730

標準正規分布 と 標準コーシー分布 を比較した場合、正規分布における 99% の確率点がコーシー分布では 87% に相当する事を確認できます。

以上です。