飽和溶存酸素濃度の推定

変数C,Clを変更した場合のシミュレーションは https://www.webr.saecanet.com/webr-dissolved-oxygen で確認出来ます。

温度 と 塩素イオン濃度 から 飽和溶存酸素濃度を求めます。

$$\begin{eqnarray}\mathrm{ln}\,C_s=-139.34411+\dfrac{1.575701\times10^5}{T}-\dfrac{6.642308\times10^7}{T^2}+\dfrac{1.243800\times10^{10}}{T^3}\\-\dfrac{8.621949\times10^{11}}{T^4}-\left\lbrace 0.031929-\dfrac{19.428}{T}-\dfrac{3867.3}{T^2}\right\rbrace\,Cl\end{eqnarray}$$

ここで、 Cs: 大気と平衡条件下(気圧が101.325kPa)での飽和溶存酸素濃度(mg/l)。 C: 0.0度から40.0度の間の温度(摂氏)。 Cl: 塩素イオン濃度(g/kg)です。

始めに関数を作成します。

library(dplyr)
fun_OxygenSolubility <- function(C, Cl) {
  T <- C + 273.15
  exp(-139.34411 + 1.575701 * 10^5 / T - 6.642308 * 10^7 / T^2 + 1.243800 * 10^10 / T^3 - 8.621949 * 10^11 / T^4 - Cl * (0.031929 - 19.428 / T + 3867.3 / T^2)) %>% round(3)
}

温度が 35度、塩素イオン濃度が 15g/kg の場合の飽和溶存酸素濃度を求めます。

fun_OxygenSolubility(C = 35, Cl = 15)
[1] 6.017

温度が 20度、塩素イオン濃度が 0 の場合の飽和溶存酸素濃度を求めます。

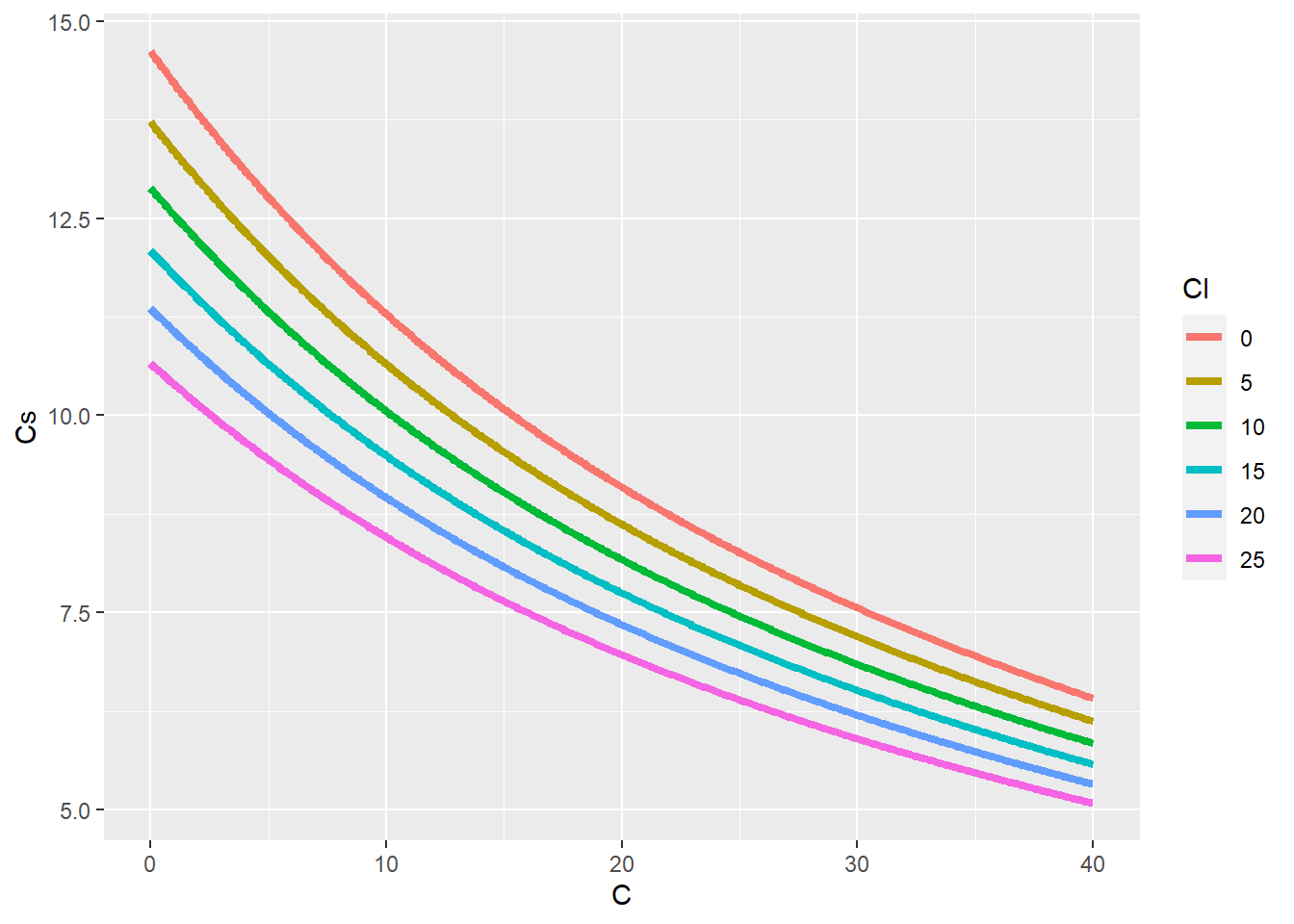
fun_OxygenSolubility(C = 20, Cl = 0)
[1] 9.092

最後に塩素イオン濃度(g/kg)が 0 5 10 15 20 25 の場合の温度ごとの飽和溶存酸素濃度をチャートにします

library(ggplot2)
C <- seq(0, 40, by = 0.1)
Cl <- seq(0, 25, by = 5)
dfsample <- data.frame(Cl = rep(Cl, each = length(C)), C = rep(C, length(Cl)))
dfsample$Cs <- dfsample %>% apply(MARGIN = 1, FUN = function(x) fun_OxygenSolubility(Cl = x[1], C = x[2]))
dfsample$Cl <- dfsample$Cl %>% factor()
dfsample %>% ggplot(mapping = aes(x = C, y = Cs, col = Cl, shape = Cl)) +
  geom_line(linewidth = 1.5)
Figure 1

飽和溶存酸素濃度は塩素イオン濃度が同じならば温度が高くなるほど低下し、温度が同じならば塩素イオン濃度が濃くなるほど低下します。

以上です。以下は参考引用資料です。

  1. American Public Health Association, American Water Works Association, Water Environment Federation, Rodger B. Baird,Andrew D. Eaton,Eugene W. Rice (2017). Standard Methods for the Examination of Water and Wastewater 20th Edition.
  2. 土木学会(2004). 環境工学公式･モデル･数値集.