関数 geom_tile {ggplot2} を利用してヒートマップを作成します。
始めにサンプルデータを作成します。
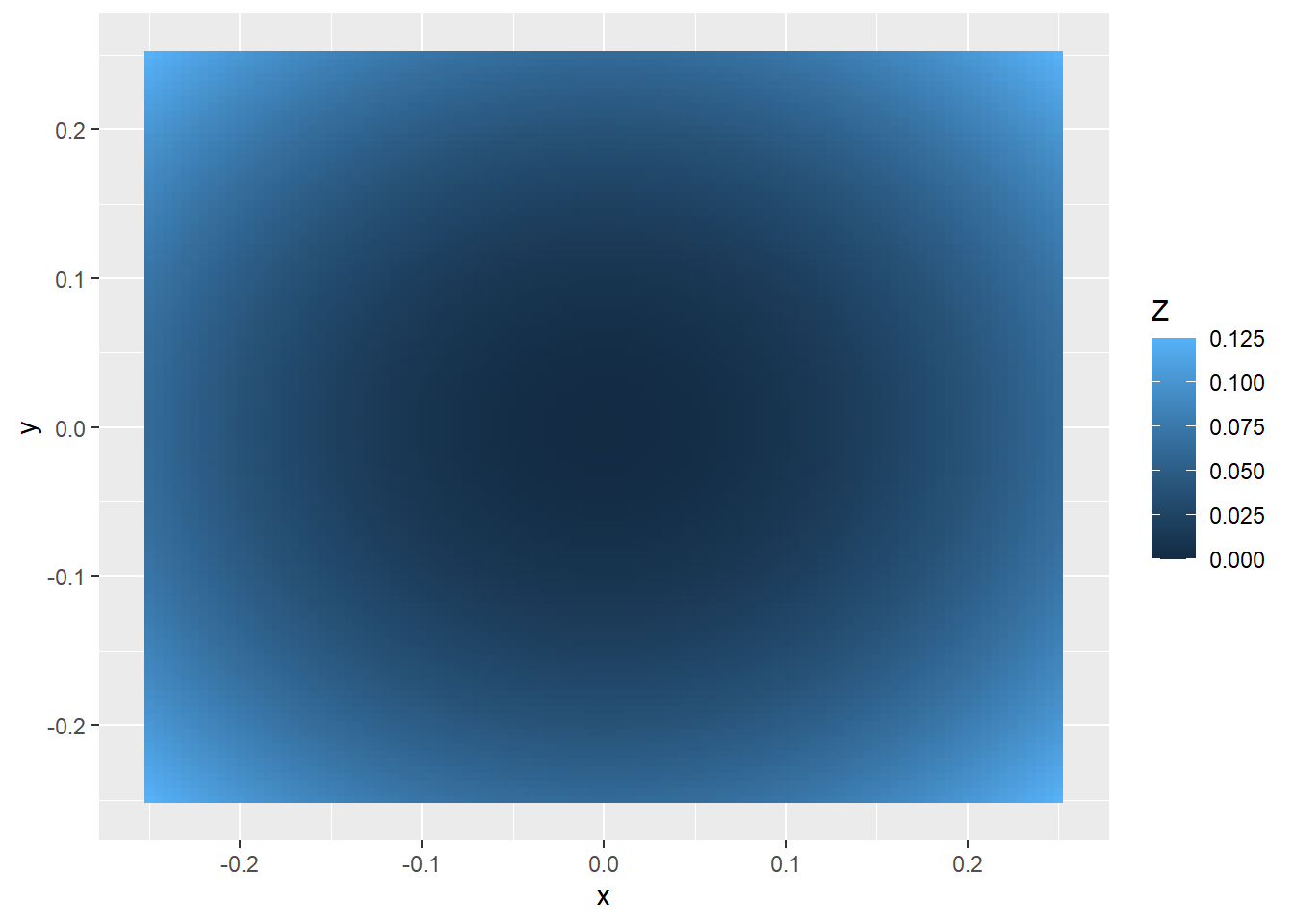
次の式の \(Z\) をヒートマップで表示します。
\[Z=x^2+y^2\]
library(dplyr)
x <- y <- seq(-0.25, 0.25, 0.005)
sampledf <- matrix(nrow = length(x), ncol = length(y)) %>%
reshape::melt() %>%
as_tibble()
colnames(sampledf) <- c("x", "y", "Z")
sampledf$Z <- sampledf %>% apply(MARGIN = 1, FUN = function(i) x[i[1]]^2 + y[i[2]]^2)
sampledf$x <- sampledf$x %>% x[.]
sampledf$y <- sampledf$y %>% y[.]
sampledf# A tibble: 10,201 × 3
x y Z
<dbl> <dbl> <dbl>
1 -0.25 -0.25 0.125
2 -0.245 -0.25 0.123
3 -0.24 -0.25 0.120
4 -0.235 -0.25 0.118
5 -0.23 -0.25 0.115
6 -0.225 -0.25 0.113
7 -0.22 -0.25 0.111
8 -0.215 -0.25 0.109
9 -0.21 -0.25 0.107
10 -0.205 -0.25 0.105
# ℹ 10,191 more rows関数 geom_tile を利用してヒートマップを作成します。
library(ggplot2)
g <- ggplot(sampledf, mapping = aes(x = x, y = y, fill = Z)) +
geom_tile()
gscale_colour_gradient2 {ggplot2} を利用してカラーグラデーションを変更し、さらに coord_fixed {ggplot2} を利用してアスペクト比を 1.0 にします。
valuelimits <- range(sampledf$Z, na.rm = T)
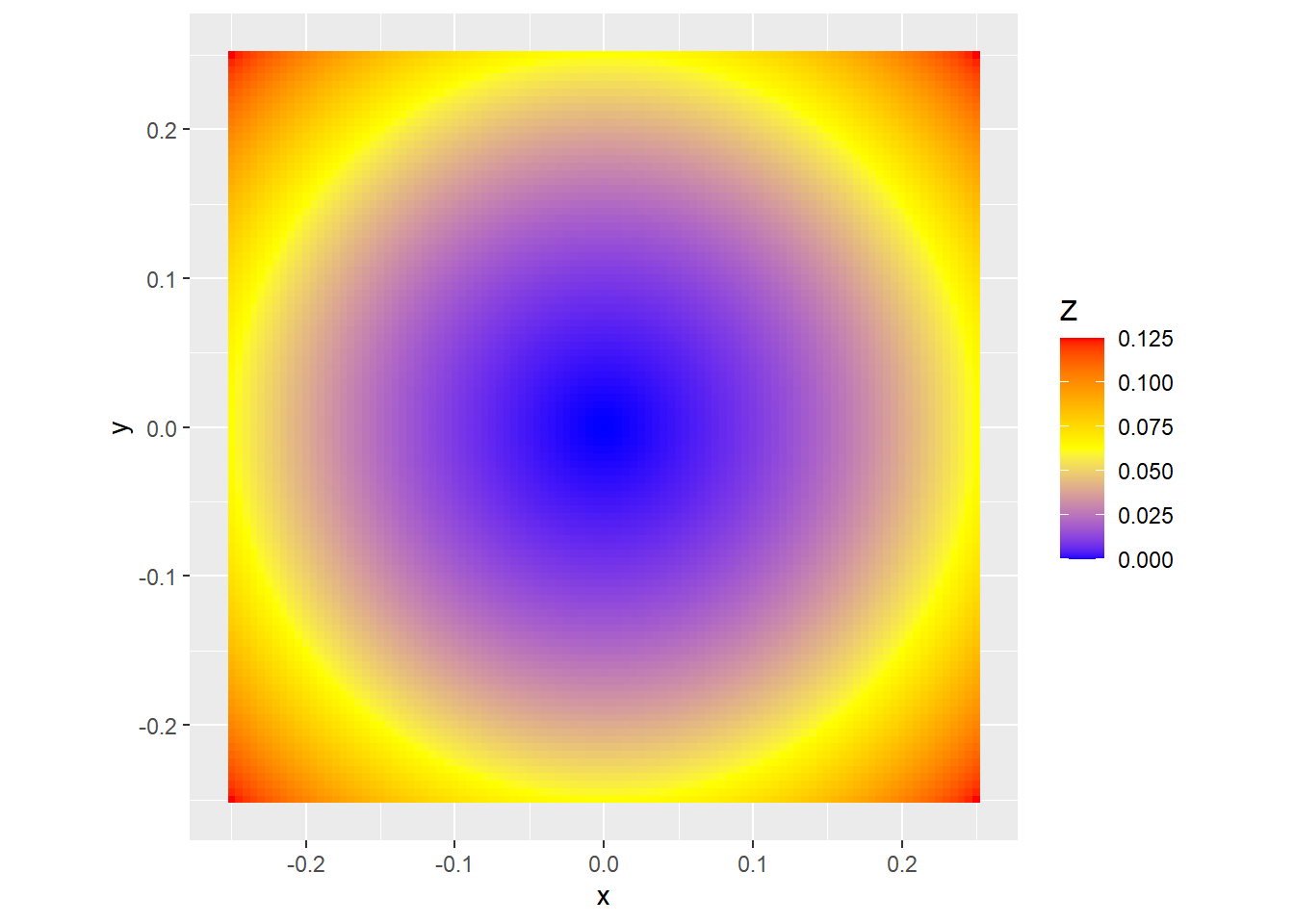
g + scale_fill_gradient2(
low = "blue", high = "red", mid = "yellow",
midpoint = valuelimits %>% mean(), limits = valuelimits
) + coord_fixed(ratio = 1)もう一つサンプルを作成します。
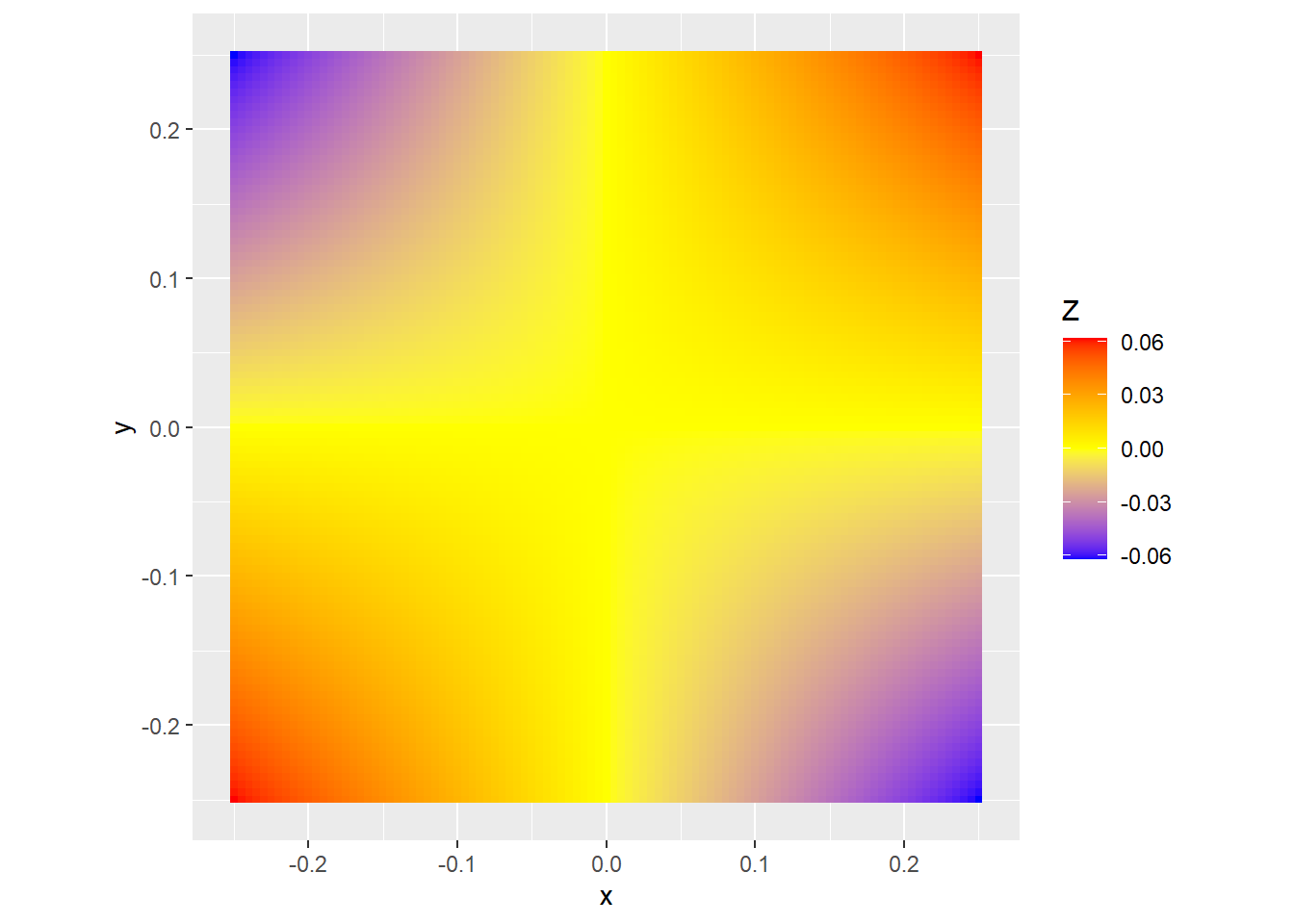
\[Z=\mathrm{sin}(x)\times y\]
sampledf <- matrix(nrow = length(x), ncol = length(y)) %>%
reshape::melt() %>%
as_tibble()
colnames(sampledf) <- c("x", "y", "Z")
sampledf$Z <- sampledf %>% apply(MARGIN = 1, FUN = function(i) sin(x[i[1]]) * y[i[2]])
sampledf$x <- sampledf$x %>% x[.]
sampledf$y <- sampledf$y %>% y[.]
valuelimits <- range(sampledf$Z, na.rm = T)
ggplot(sampledf, mapping = aes(x = x, y = y, fill = Z)) +
geom_tile() +
scale_fill_gradient2(
low = "blue", high = "red", mid = "yellow",
midpoint = valuelimits %>% mean(), limits = valuelimits
) +
coord_fixed(ratio = 1)以上です。