Rで粒子フィルタによる状態の推定

粒子フィルタ(パーティクルフィルタ、モンテカルロフィルタ)による状態の推定です。

以降の数式や導出は全てこちらの論文からから引用しています。

Genshiro Kitagawa(1998),A Self-Organizing State-Space Model,Journal of the American Statistical Association, Vol. 93, No. 443 (Sep., 1998), pp. 1203-1215 (以降、Kitagawa(1998))

また、Rコードはこちらの資料を参照引用しています。

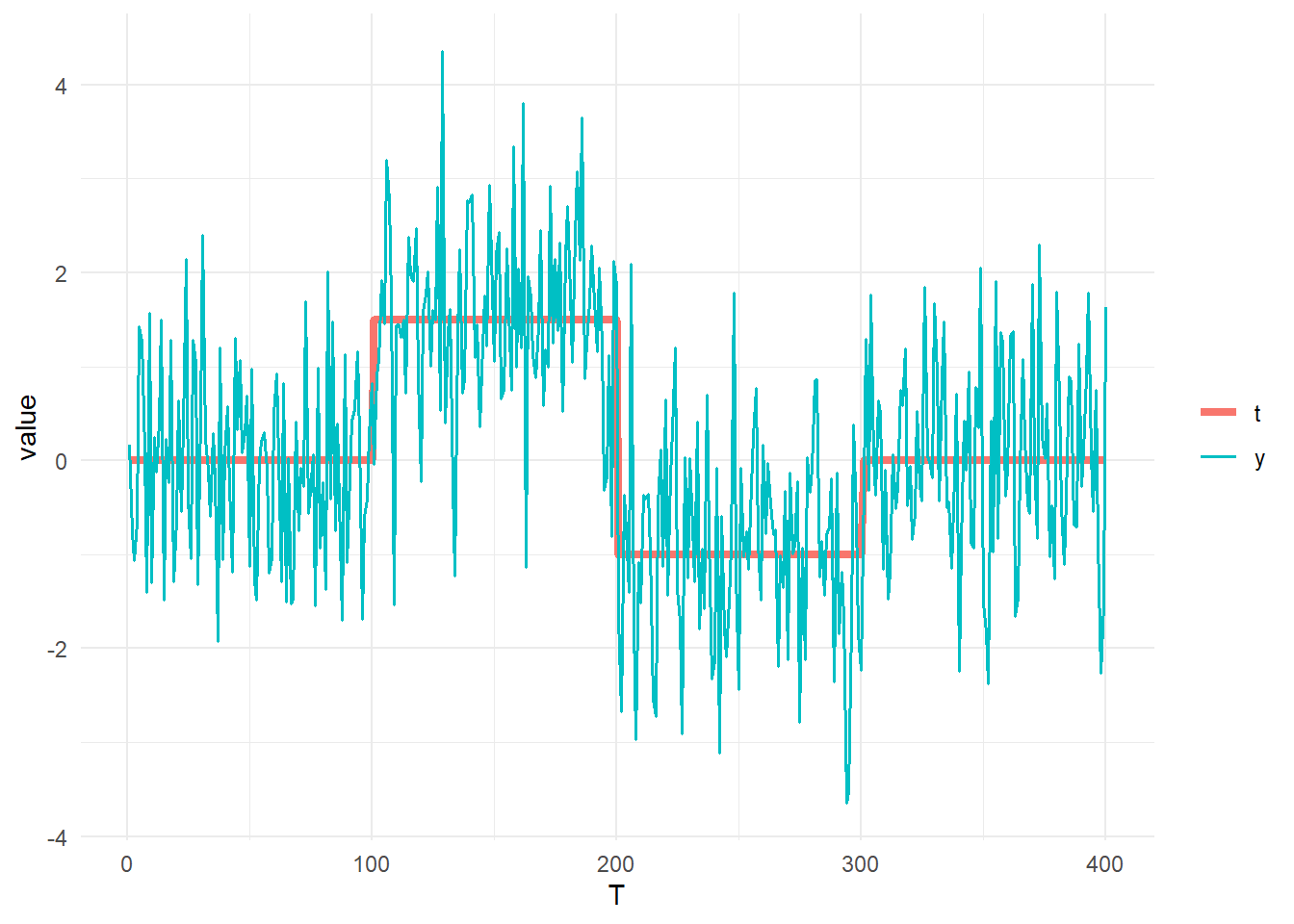
http://www.mi.u-tokyo.ac.jp/mds-oudan/lecture_document_2019_math7/2018%E5%B9%B4%E5%BA%A6%E7%89%88/%E6%99%82%E7%B3%BB%E5%88%97%E8%A7%A3%E6%9E%90%EF%BC%88%EF%BC%91%EF%BC%93%EF%BC%89_%E9%85%8D%E5%B8%83%E7%94%A8.pdf (以降、北川(2019))

始めに Kitagawa(1998), p.1206 のサンプルデータ \(y_n\) を作成します。

\[y_n\sim\mathrm{N}(t_n,1)\]

ここで、

\[\begin{eqnarray} t_n = \begin{cases} 0 & n=1,\dots,100 \\ 1.5 & n=101,\dots,200\\ -1 & n=201,\dots,300\\ 0 & n=301,\dots,400 \end{cases} \end{eqnarray}\]

library(tidyr)
library(ggplot2)
seed <- 20240610
set.seed(seed)
t <- rep(0, 400)
t[101:200] <- 1.5
t[201:300] <- -1
T <- length(t)
y <- rnorm(T, mean = t, sd = 1)
tidydf <- data.frame(T = seq(T), t, y) %>% gather(key = "key", value = "value", colnames(.)[-1])
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  theme_minimal() +
  scale_linewidth_manual(values = c(1.5, 0.6)) +
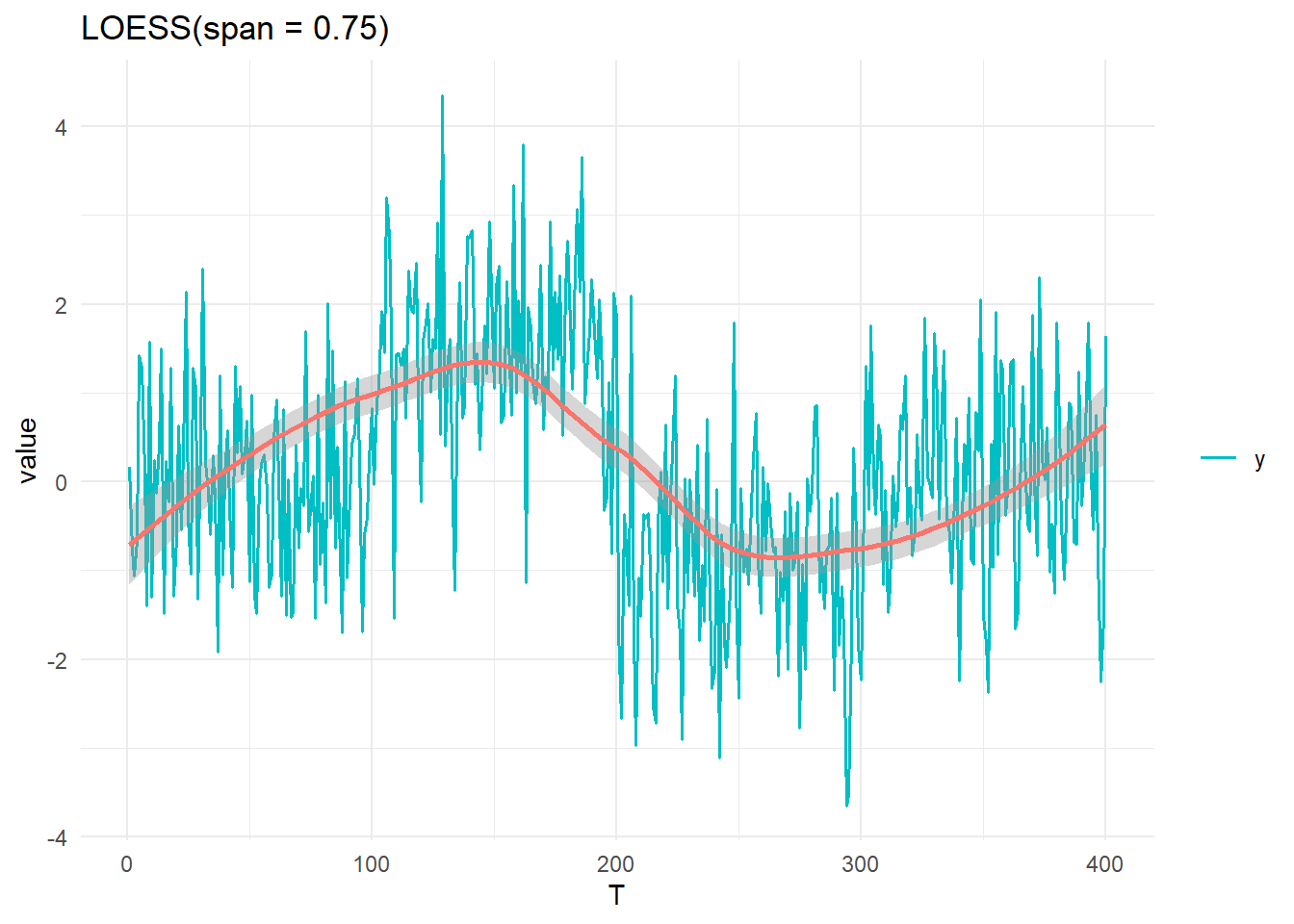
  theme(legend.title = element_blank())

参考として LOESS近似曲線 を確認します。1つ目はスパンをデフォルトの 0.75 とします。

linecol <- scales::hue_pal()(2)
tidydf <- data.frame(T = seq(T), y) %>% gather(key = "key", value = "value", colnames(.)[-1])
ggplot(data = tidydf, aes(x = T, y = value, col = key)) +
  geom_line(linewidth = 0.6) +
  theme_minimal() +
  theme(legend.title = element_blank()) +
  geom_smooth(method = "loess", col = linecol[1], span = 0.75) +
  scale_color_manual(values = linecol[2]) +
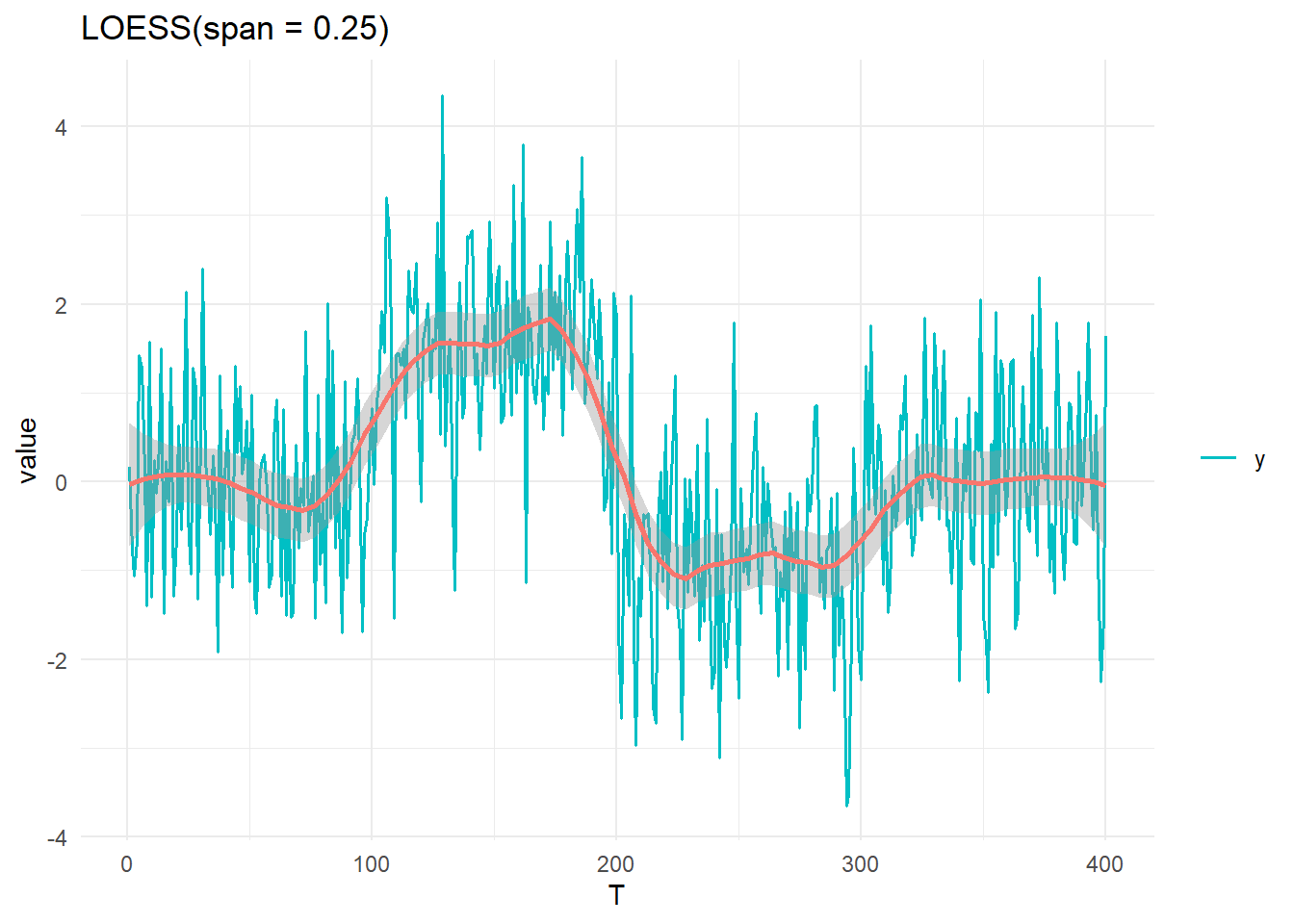
  labs(title = "LOESS(span = 0.75)")

`geom_smooth()` using formula = 'y ~ x'

loess(span = 0.25) とした場合は、

ggplot(data = tidydf, aes(x = T, y = value, col = key)) +
  geom_line(linewidth = 0.6) +
  theme_minimal() +
  theme(legend.title = element_blank()) +
  geom_smooth(method = "loess", col = linecol[1], span = 0.25) +
  scale_color_manual(values = linecol[2]) +
  labs(title = "LOESS(span = 0.25)")

`geom_smooth()` using formula = 'y ~ x'

\(t_n\) の平均値を推定するために、次の一次のトレンドモデルを考えます。

\[\begin{eqnarray} x_n&=&x_{n-1}+\nu_n\\ y_n&=& x_n+\omega_n\end{eqnarray} \] ここで、\(\omega_n\) は平均が 0、分散が 1 の観測ノイズ(ホワイトガウスノイズ)。\(\nu_n\) はコーシー分布 \[\nu_n\sim C(\nu;\tau^2)\] に従うシステムノイズ。システムノイズの密度関数は以下の通り。

\[p(\nu;\tau^2)=\dfrac{1}{\pi}\dfrac{\tau}{\nu^2+\tau^2}\] \(\nu^2\) はコーシー分布の位置パラメータ(ロケーション)、\(\tau^2\) は尺度パラメータ(分散パラメータ、スケール)。

「システムノイズにコーシー分布を用いると，状態の時間変化について前時刻とほぼ同じであるが稀にジャンプが生じる状況を表すことになる」
出典: https://www.cirje.e.u-tokyo.ac.jp/research/reports/R-15-3.pdf#page=322

状態とパラメータの同時推定のため、2次の状態ベクトルを考えます。

\[\mathbf{z}_n=\begin{bmatrix}x_n\\\mathrm{log}_{10}\tau_n^2\end{bmatrix}\]

分散パラメータ \(\tau^2\) を正の数とするため、拡大状態ベクトルでは \(\tau^2\) ではなく \(\mathrm{log}_{10}\tau_n^2\) と変換しています。

よって、状態空間モデル \(\mathbf{z}_n\) は以下の通りに与えられます。

状態

\[\mathbf{z}_n=\begin{bmatrix}x_n\\\mathrm{log}_{10}\tau_n^2\end{bmatrix}=\begin{bmatrix}x_{n-1}\\\mathrm{log}_{10}\tau_{n-1}^2\end{bmatrix}+\begin{bmatrix}1\\0\end{bmatrix}\nu_n\quad \nu\sim C(\nu;\tau_{n-1}^2)\]

観測

\[y_n=\begin{bmatrix}1,0\end{bmatrix}\begin{bmatrix}x_n\\\mathrm{log}_{10}\tau_n^2\end{bmatrix}+\omega_n\]

初期状態 \(\mathbf{z}_0=(x_0,\mathrm{log}_{10}\tau_0^2)^t\) として \(x_0\) と \(\mathrm{log}_{10}\tau_0^2\) はそれぞれ \(\mathrm{N}(0,4)\) の正規分布と \(\mathrm{U}(-8,-2)\) の一様分布に従うとします。

なお、粒子の数は Kitagawa(1998), p.1206 では201個とされていますが 北川(2019) では1万個とされていますので本ページでは1万個とします。

m <- 10000

それでは、初期状態を作成します。なお以降 \(x\) は 北川(2019) に合わせて変数 xf とします。また、観測ノイズの初期状態 \(\omega_0\) は観測値の標準偏差の 0.5倍 から 2倍の範囲の一様分布から作成します。

set.seed(seed)
xf <- rnorm(m, mean = 0, sd = 4)
log10tau2 <- runif(m, min = -8, max = -2)
w <- runif(m, min = sd(y) * 0.5, max = sd(y) * 2)

フィルタ分布 \(x\) とパラメータ \(\mathrm{log}_{10}\tau_n^2\)、\(\omega_n\) を格納する配列を作成します。

pfresult <- array(
  data = NA,
  dim = c(m, T, 3),
  dimnames = list(
    NULL,
    NULL,
    c("xf", "log10tau2", "w")
  )
)

以降、予測、尤度の算出、リサンプリング を繰り返します。

set.seed(seed)
for (ii in seq(T)) {
  v <- rcauchy(n = m, location = 0, scale = sqrt(10^log10tau2))
  xp <- xf + v
  alpha <- dnorm(y[ii] - xp, mean = 0, sd = w) %>%
    {
      . / sum(.)
    }
  rs <- sample(seq(m), prob = alpha, replace = T)
  xf <- xp[rs]
  log10tau2 <- log10tau2[rs]
  w <- w[rs]
  pfresult[, ii, "xf"] <- xf
  pfresult[, ii, "log10tau2"] <- log10tau2
  pfresult[, ii, "w"] <- w
}

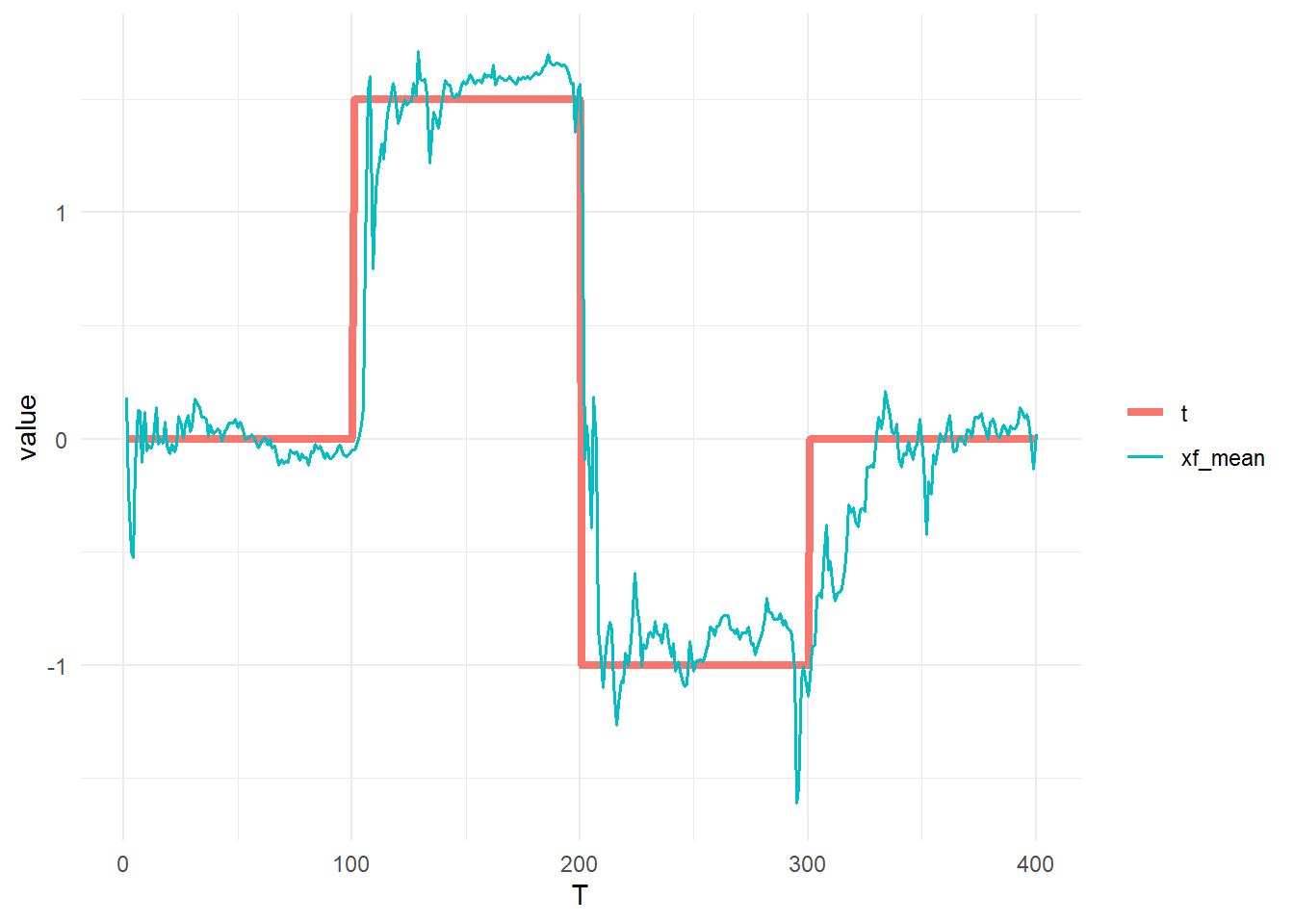
最初は t(状態) と推定値 xf_mean を比較します。

xf_mean <- apply(X = pfresult[, , "xf"], MARGIN = 2, FUN = function(x) mean(x))
tidydf <- data.frame(T = seq(T), t, xf_mean) %>% gather(key = "key", value = "value", colnames(.)[-1])
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  theme_minimal() +
  scale_linewidth_manual(values = c(1.5, 0.7)) +
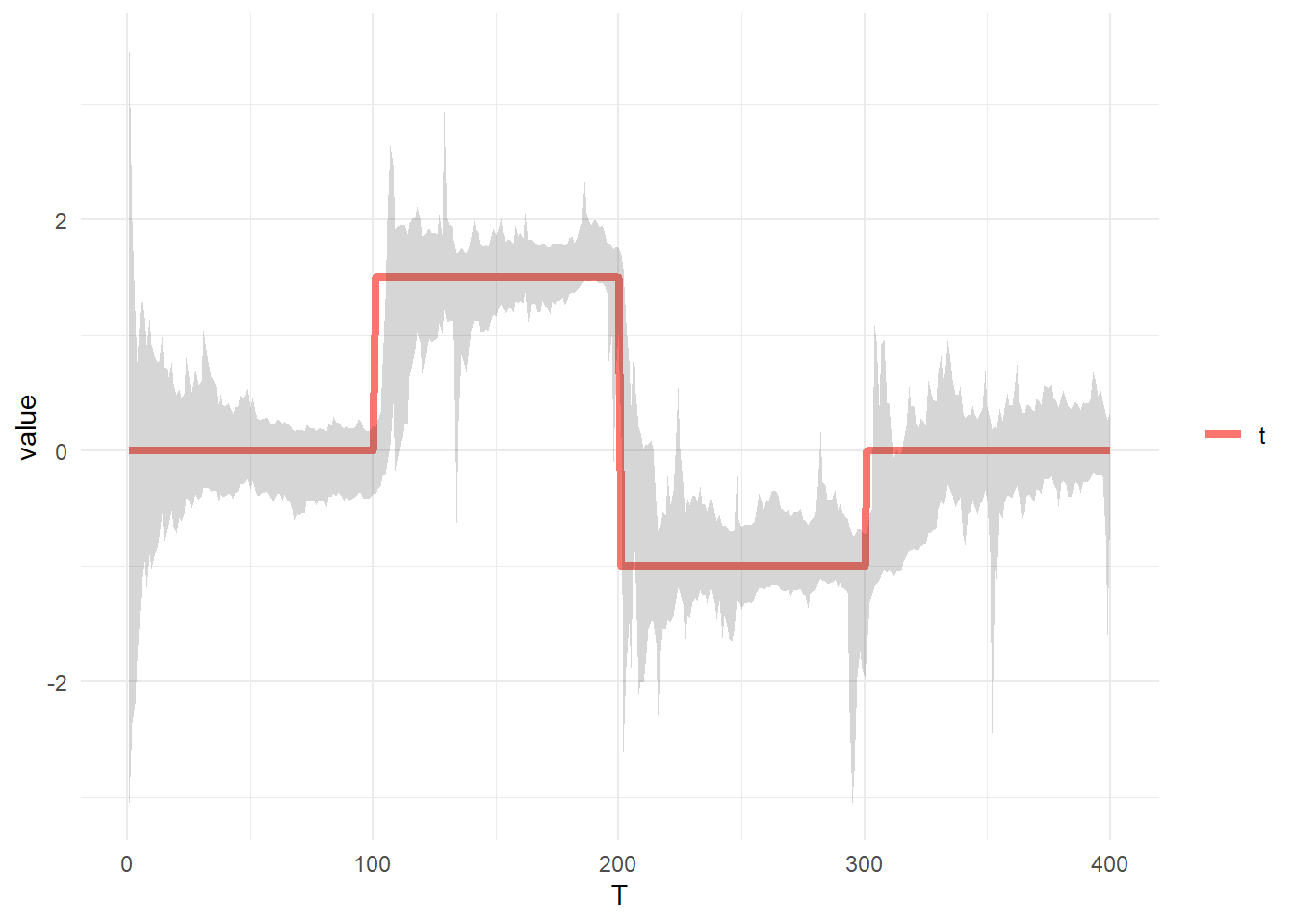
  theme(legend.title = element_blank())

続いて t(状態) と xf の 95%信用区間 を比較します。

xf_quantile <- apply(X = pfresult[, , "xf"], MARGIN = 2, FUN = function(x) quantile(x = x, probs = c(0.025, 0.975)))
tidydf <- data.frame(T = seq(T), t) %>% gather(key = "key", value = "value", colnames(.)[-1])
tidydf_ribbon <- t(xf_quantile) %>% data.frame(T = seq(T), ., check.names = F)
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  geom_ribbon(aes(x = tidydf_ribbon$T, ymin = tidydf_ribbon$`2.5%`, ymax = tidydf_ribbon$`97.5%`), alpha = 0.2) +
  theme_minimal() +
  scale_linewidth_manual(values = 1.5) +
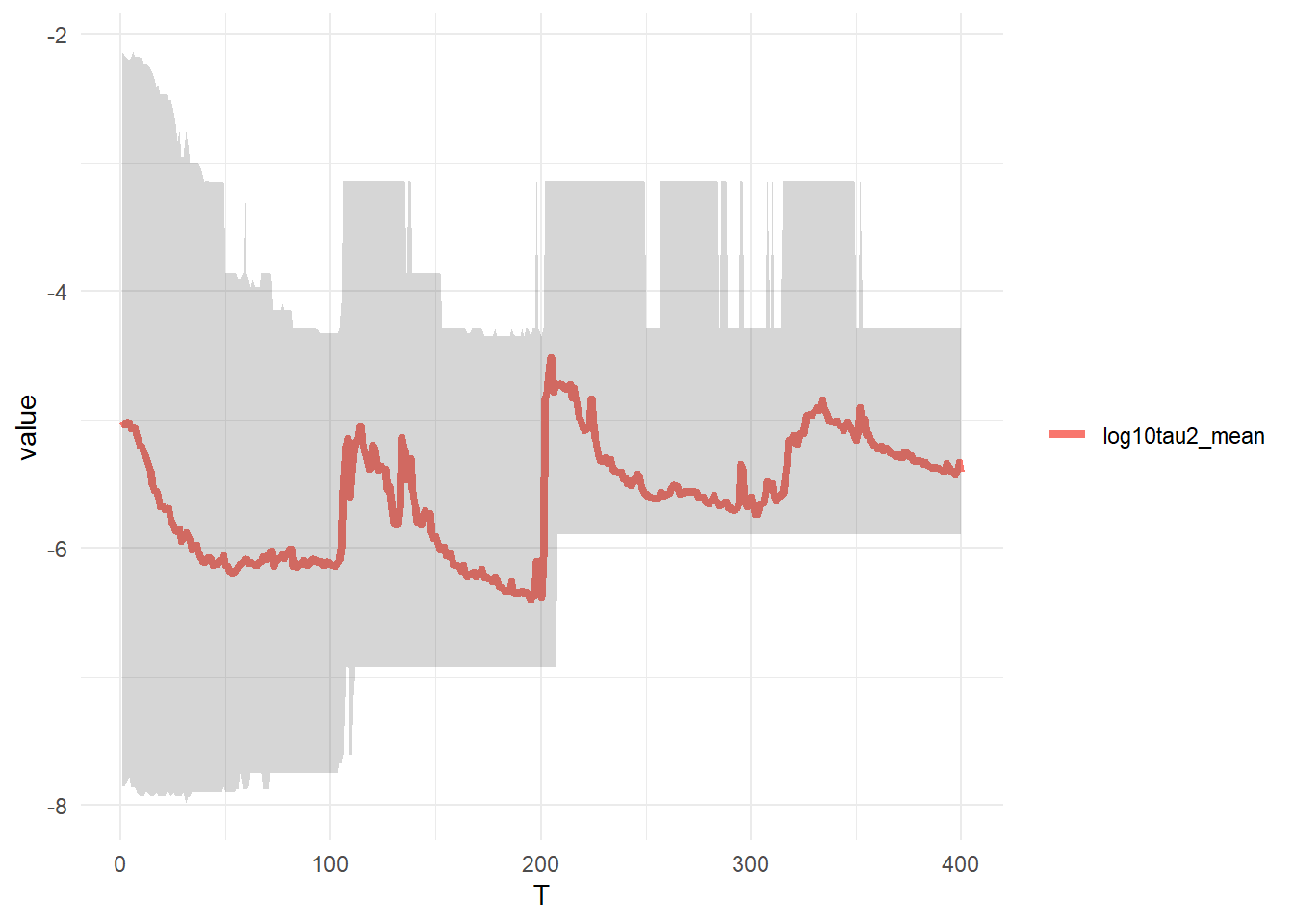
  theme(legend.title = element_blank())

同時に推定したパラメータ \(\mathrm{log}_{10}\tau_n^2\) を確認します。

log10tau2_mean <- apply(X = pfresult[, , "log10tau2"], MARGIN = 2, FUN = function(x) mean(x))
log10tau2_quantile <- apply(X = pfresult[, , "log10tau2"], MARGIN = 2, FUN = function(x) quantile(x, probs = c(0.025, 0.975)))
tidydf <- data.frame(T = seq(T), log10tau2_mean) %>% gather(key = "key", value = "value", colnames(.)[-1])
tidydf_ribbon <- t(log10tau2_quantile) %>% data.frame(T = seq(T), ., check.names = F)
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  theme_minimal() +
  geom_ribbon(aes(x = tidydf_ribbon$T, ymin = tidydf_ribbon$`2.5%`, ymax = tidydf_ribbon$`97.5%`), alpha = 0.2) +
  theme_minimal() +
  scale_linewidth_manual(values = 1.5) +
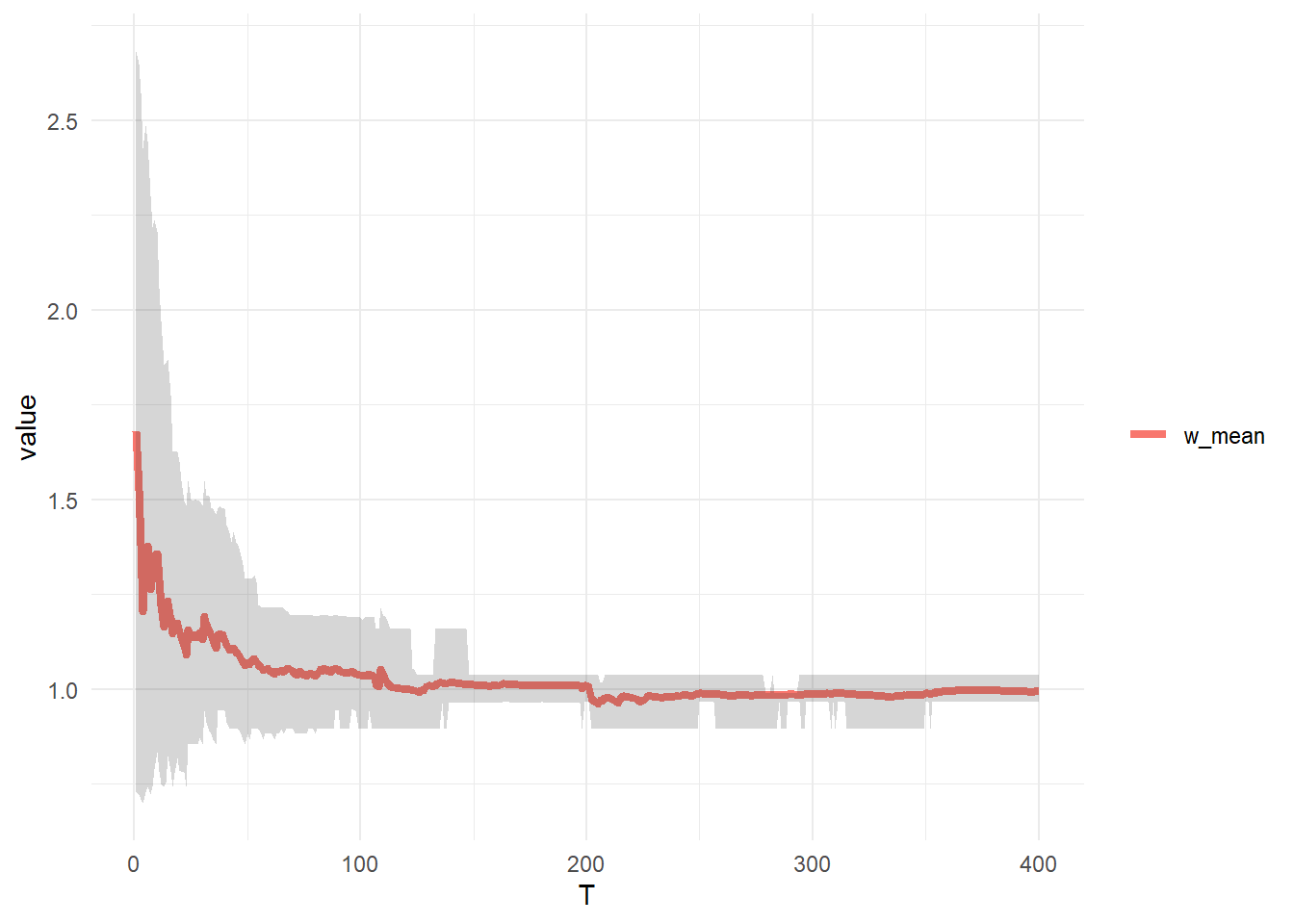
  theme(legend.title = element_blank())

同じく同時に推定したパラメータ \(\omega_n\) を確認します。

w_mean <- apply(X = pfresult[, , "w"], MARGIN = 2, FUN = function(x) mean(x))
w_quantile <- apply(X = pfresult[, , "w"], MARGIN = 2, FUN = function(x) quantile(x, probs = c(0.025, 0.975)))
tidydf <- data.frame(T = seq(T), w_mean) %>% gather(key = "key", value = "value", colnames(.)[-1])
tidydf_ribbon <- t(w_quantile) %>% data.frame(T = seq(T), ., check.names = F)
ggplot() +
  geom_line(data = tidydf, aes(x = T, y = value, col = key, linewidth = key)) +
  theme_minimal() +
  geom_ribbon(aes(x = tidydf_ribbon$T, ymin = tidydf_ribbon$`2.5%`, ymax = tidydf_ribbon$`97.5%`), alpha = 0.2) +
  theme_minimal() +
  scale_linewidth_manual(values = 1.5) +
  theme(legend.title = element_blank())

以上です。