Rの関数 breakpoints {strucchange} を利用して時系列データの 構造変化点(ブレイクポイント) の抽出を試みます。
以下の資料を参照引用しています。
- https://cran.r-project.org/web/packages/strucchange/strucchange.pdf
- https://cran.r-project.org/web/packages/strucchange/vignettes/strucchange-intro.pdf
始めに関数のコードを確認します。
library(strucchange)
methods(breakpoints)[1] breakpoints.breakpointsfull* breakpoints.formula*
[3] breakpoints.Fstats*
see '?methods' for accessing help and source code以下はコメントを挿入しました関数 breakpoints.formula のコードです。
function(formula, h = 0.15, breaks = NULL, data = list(), hpc = c(
"none",
"foreach"
), ...) {
# model.frame関数を用いて、与えられたformulaとdataからモデルフレームmfを作成します。
# モデルフレームmfは、モデルで使用される変数を含んだデータフレームです。
# モデルの設計行列と応答変数を準備するステップです。
mf <- model.frame(formula, data = data)
# model.response関数を用いて、モデルフレームmfから応答変数yを抽出します。
y <- model.response(mf)
# terms関数を用いて、formulaとdataからモデル項modeltermsを抽出します。
# モデル項は、モデルで使用される説明変数の関係性を定義します。
modelterms <- terms(formula, data = data)
# model.matrix関数を用いて、モデル項modeltermsとdataから計画行列Xを作成します。
# 計画行列Xは、回帰モデルにおける説明変数の値を格納した行列です。
# 線形モデル Y = Xβ + ε におけるXです。
X <- model.matrix(modelterms, data = data)
# nrow関数を用いて、計画行列Xの行数(観測数)をnに格納します。
n <- nrow(X)
# ncol関数を用いて、計画行列Xの列数(説明変数の数)をkに格納します。
k <- ncol(X)
# intercept_onlyは、計画行列Xが切片項(定数項)のみからなるかどうかを判定します。
# all.equal(as.vector(X), rep(1L, n)) は、Xの全ての要素が1であるベクトルと等しいかを比較します。
# 切片のみのモデル(平均値モデル)かどうかを判定します。
intercept_only <- isTRUE(all.equal(as.vector(X), rep(
1L,
n
)))
# もし最小セグメントサイズhがNULLならば、hをk + 1(説明変数の数 + 1)に設定します。
# これは、最小セグメントサイズが説明変数の数よりも小さくならないようにするためのデフォルト設定です。
if (is.null(h)) {
h <- k + 1
}
# もしhが1より小さければ、hをfloor(n * h)(観測数nにhを乗じて小数点以下を切り捨てた値)に設定します。
# hが割合で与えられた場合に、実際の観測数に変換します。
if (h < 1) {
h <- floor(n * h)
}
# もしhが説明変数の数k以下であれば、エラーメッセージを出力して処理を停止します。
if (h <= k) {
stop("minimum segment size must be greater than the number of regressors")
}
# もしhがfloor(n/2)(観測数nの半分を小数点以下切り捨てた値)より大きければ、エラーメッセージを出力して処理を停止します。
if (h > floor(n / 2)) {
stop("minimum segment size must be smaller than half the number of observations")
}
# もしbreaksがNULLならば、breaksをceiling(n/h) - 2に設定します。
if (is.null(breaks)) {
breaks <- ceiling(n / h) - 2
}
# breaksがNULLでない場合(ユーザーがbreaksを指定した場合)の処理
else {
# もしbreaksが1より小さければ、breaksを1に設定し、警告メッセージを表示します。
# ブレイクポイントの数は最低でも1つ必要であるため、下限を設定します。
if (breaks < 1) {
breaks <- 1
warning("number of breaks must be at least 1")
}
# もしbreaksがceiling(n/h) - 2より大きければ、breaksをceiling(n/h) - 2に設定し、警告メッセージを表示します。
if (breaks > ceiling(n / h) - 2) {
breaks0 <- breaks
breaks <- ceiling(n / h) - 2
warning(sprintf(
"requested number of breaks = %i too large, changed to %i",
breaks0, breaks
))
}
}
# hpc引数の値を部分一致で評価し、有効な値("none"または"foreach")のいずれかに設定します。
hpc <- match.arg(hpc)
# もしhpcが"foreach"ならば、並列計算環境の設定を試みます。
if (hpc == "foreach") {
# foreachパッケージがインストールされているか確認します。
if (requireNamespace("foreach")) {
# foreachパッケージの`%dopar%`演算子を変数に代入します。これにより、並列処理が可能になります。
`%dopar%` <- foreach::`%dopar%`
}
# foreachパッケージがインストールされていない場合
else {
# 警告メッセージを表示し、hpcを"none"に設定して、並列計算を無効にします。
warning("High perfomance computing (hpc) support with 'foreach' package is not available, foreach is not installed.")
hpc <- "none"
}
}
# 関数RSSiは、開始点iからnまでのデータを使用して、累積二乗再帰残差を計算します。
# 引数 i: 計算を開始するデータのインデックス。
# 目的: 構造変化の可能性を評価するために、各時点から開始して計算される累積二乗再帰残差を求める。
# 再帰残差は、時点tまでのデータに基づいて推定されたモデルを用いて、時点tの予測誤差を計算したもの。
# intercept_onlyが真の場合、平均値モデルに対する再帰残差の二乗和を計算します。
# intercept_onlyが偽の場合、recresid関数を用いて線形モデルに対する再帰残差を計算します。
RSSi <- function(i) {
# ssr (squared recursive residuals): 再帰残差の二乗を格納する変数。
ssr <- if (intercept_only) {
# 切片のみのモデルの場合
# y[i:n]は、時点iからnまでの応答変数のベクトル。
# cumsum(y[i:n])/(1L:(n - i + 1L)) は、時点iから始まる累積平均。
# (y[i:n] - cumsum(y[i:n])/(1L:(n - i + 1L)))[-1L] は、各時点の応答変数から累積平均を引いたベクトル(最初を除く)。
# sqrt(1L + 1L/(1L:(n - i))) は、再帰残差の分散を安定化させるための調整項。
(y[i:n] - cumsum(y[i:n]) / (1L:(n - i + 1L)))[-1L] *
sqrt(1L + 1L / (1L:(n - i)))
} else {
# 一般の線形モデルの場合
# recresid関数を用いて、計画行列X[i:n, , drop = FALSE]と応答変数y[i:n]から再帰残差を計算します。
recresid(X[i:n, , drop = FALSE], y[i:n], ...)
}
# c(rep(NA, k), cumsum(ssr^2)) は、結果ベクトルを生成します。
# rep(NA, k) は、最初のk個の要素をNA(欠損値)で埋めます。これは、最初のk個の再帰残差が計算できないためです(初期値問題)。
# cumsum(ssr^2) は、再帰残差の二乗値の累積和を計算します。これが、時点iから始まる累積二乗再帰残差系列です。
c(rep(NA, k), cumsum(ssr^2))
}
# RSS.triangは、開始点を1から(n - h + 1)まで変化させてRSSi関数を適用した結果を格納します。
# hpc == "none" の場合、sapply関数を用いて逐次的に計算します。
# hpc == "foreach" の場合、foreachパッケージを用いて並列計算を行います。
# 結果はリスト形式で格納されます。各要素は、対応する開始点に対する累積二乗再帰残差ベクトルです。
RSS.triang <- if (hpc == "none") {
sapply(1:(n - h + 1), RSSi)
} else {
foreach::foreach(i = 1:(n - h + 1)) %dopar% RSSi(i)
}
# 関数RSSは、開始点iと終了点jを指定して、対応する累積二乗再帰残差の値を取得します。
# 引数 i: セグメントの開始点。
# 引数 j: セグメントの終了点。
# 目的: 特定のセグメントにおける累積二乗再帰残差の値を取り出す。
# RSS.triang[[i]]は、開始点がiである場合の累積二乗再帰残差ベクトル。
# RSS.triang[[i]][j - i + 1] は、そのベクトルの(j - i + 1)番目の要素、つまり時点jにおける累積二乗再帰残差の値。
# 時点iからjまでのセグメントにおけるモデルの不適合度合い(残差変動の大きさ)を評価するための指標を取得します。
RSS <- function(i, j) RSS.triang[[i]][j - i + 1]
# indexは、ブレイクポイントの探索範囲を定義します。
# h:(n - h) は、hから(n - h)までの整数ベクトル。
# 最小セグメントサイズhを考慮し、最初と最後のh個の観測を除外した範囲でブレイクポイントを探します。
index <- h:(n - h)
# break.RSSは、各時点i (indexの範囲内) を単一のブレイクポイントとした場合のRSS値を計算します。
# sapply(index, function(i) RSS(1, i)) は、indexの各要素iに対して、RSS(1, i)を計算します。
# RSS(1, i) は、データ全体(開始点1から)を時点iで分割した場合の、最初のセグメントのRSS値(実際には累積二乗再帰残差の値)。
break.RSS <- sapply(index, function(i) RSS(1, i))
# RSS.tableは、ブレイクポイントのインデックスとその時のRSS値を格納する行列を作成します。
# cbind(index, break.RSS) は、indexとbreak.RSSを列方向に結合します。
RSS.table <- cbind(index, break.RSS)
# 行の名前をインデックスの値に設定します。
rownames(RSS.table) <- as.character(index)
# 関数extend.RSS.tableは、RSS.tableを拡張して、複数のブレイクポイントを考慮したRSS値を計算します。
# 引数 RSS.table: 現在までのブレイクポイント数で計算されたRSSテーブル。
# 引数 breaks: 考慮するブレイクポイントの総数。
# 目的: 複数のブレイクポイントを逐次的に追加しながら、最適なブレイクポイントの位置とそれに対応するRSS値を計算し、テーブルを拡張する。
# 動的計画法的なアプローチで、ブレイクポイントを一つずつ増やしながら、各ブレイクポイント位置でのRSSを最小化する位置を探索します。
# m個のブレイクポイントの場合、(m-1)個のブレイクポイントの場合の結果を再利用し、効率的に計算を行います。
# RSS値の減少量を見ることで、追加されたブレイクポイントがモデルの改善にどれだけ寄与しているかを判断できます。
extend.RSS.table <- function(RSS.table, breaks) {
# もし要求されたブレイクポイント数breaksの2倍が、現在のRSS.tableの列数よりも大きければ、
if ((breaks * 2) > ncol(RSS.table)) {
# ブレイクポイント数を1からbreaksまで増やしてループ処理を行います。
for (m in (ncol(RSS.table) / 2 + 1):breaks) {
# my.indexは、m個目のブレイクポイントの探索範囲を定義します。
my.index <- (m * h):(n - h)
# my.RSS.tableは、(m-1)個目のブレイクポイントまでの情報が格納されたRSS.tableから、必要な列を抽出します。
# c((m - 1) * 2 - 1, (m - 1) * 2) は、(m-1)番目のブレイクポイントとそのRSS値の列インデックスを指定します。
my.RSS.table <- RSS.table[, c(
(m - 1) * 2 - 1,
(m - 1) * 2
)]
# my.RSS.tableに、m番目のブレイクポイントとRSS値を格納するためのNA列を追加します。
my.RSS.table <- cbind(my.RSS.table, NA, NA)
# my.indexの各要素i(m番目のブレイクポイントの候補位置)についてループ処理を行います。
for (i in my.index) {
# pot.indexは、(m-1)番目のブレイクポイントの候補位置の範囲を定義します。
pot.index <- ((m - 1) * h):(i - h)
# break.RSSは、各pot.indexのjを(m-1)番目のブレイクポイントとした場合の、m個のブレイクポイントを持つモデルのRSS値を計算します。
# my.RSS.table[as.character(j), 2] は、(m-1)個のブレイクポイントを持つモデルで、(m-1)番目のブレイクポイントがjの位置にある場合のRSS値。
# RSS(j + 1, i) は、j+1からiまでのセグメントのRSS値(実際には累積二乗再帰残差の値)。
break.RSS <- sapply(pot.index, function(j) {
my.RSS.table[
as.character(j),
2
] + RSS(j + 1, i)
})
# optは、break.RSSの中で最小値となるインデックス(最適な(m-1)番目のブレイクポイントの位置)を求めます。
opt <- which.min(break.RSS)
# my.RSS.tableのi行目の3, 4列目に、最適な(m-1)番目のブレイクポイントの位置pot.index[opt]と、その時の最小RSS値break.RSS[opt]を格納します。
my.RSS.table[as.character(i), 3:4] <- c(
pot.index[opt],
break.RSS[opt]
)
}
# RSS.tableに、計算されたm番目のブレイクポイントとRSS値の列を追加して拡張します。
RSS.table <- cbind(RSS.table, my.RSS.table[
,
3:4
])
}
# RSS.tableの列名を設定します。
colnames(RSS.table) <- as.vector(rbind(paste("break",
1:breaks,
sep = ""
), paste("RSS", 1:breaks, sep = "")))
}
# 拡張されたRSS.tableを返します。
return(RSS.table)
}
# extend.RSS.table関数を用いて、RSS.tableをブレイクポイント数breaksまで拡張します。
RSS.table <- extend.RSS.table(RSS.table, breaks)
# 関数extract.breaksは、RSS.tableから最適なブレイクポイントの位置を抽出します。
# 引数 RSS.table: extend.RSS.table関数で計算されたRSSテーブル。
# 引数 breaks: 抽出するブレイクポイントの数。
# 目的: 計算されたRSSテーブルから、指定された数のブレイクポイントに対する最適な位置を特定する。
# RSSテーブルの中で、指定されたブレイクポイント数において、総RSSを最小にするブレイクポイントの組み合わせを探し出す。
# モデルの当てはまりを最も改善するブレイクポイントの位置を特定します。
# これらのブレイクポイントは、データにおける構造変化が最も強く示唆される時点と解釈できます。
extract.breaks <- function(RSS.table, breaks) {
# もし要求されたブレイクポイント数breaksの2倍が、RSS.tableの列数よりも大きければ、エラーメッセージを出力して処理を停止します。
if ((breaks * 2) > ncol(RSS.table)) {
stop("compute RSS.table with enough breaks before")
}
# indexは、RSS.tableの最初の列(インデックス)を抽出します。
index <- RSS.table[, 1, drop = TRUE]
# break.RSSは、各時点i (indexの範囲内) を最後のブレイクポイントとした場合の、breaks個のブレイクポイントを持つモデルのRSS値を計算します。
# RSS.table[as.character(i), breaks * 2] は、iを最後のブレイクポイントとした場合の、breaks個のブレイクポイントを持つモデルの、最後のブレイクポイントまでの累積RSS値。
# RSS(i + 1, n) は、i+1からnまでの最後のセグメントのRSS値(実際には累積二乗再帰残差の値)。
break.RSS <- sapply(index, function(i) {
RSS.table[
as.character(i),
breaks * 2
] + RSS(i + 1, n)
})
# optは、break.RSSの中で最小値となるインデックス(最適な最後のブレイクポイントの位置)を求めます。
opt <- index[which.min(break.RSS)]
# もしブレイクポイント数が1より大きければ、
if (breaks > 1) {
# ブレイクポイント数をbreaksから2まで減らしながら逆順にループ処理を行います。
for (i in ((breaks:2) * 2 - 1)) {
# 最適なブレイクポイントの位置optを更新します。
# RSS.table[as.character(opt[1]), i] は、既に求まっている最適ブレイクポイントopt[1]の前のブレイクポイントの位置をRSS.tableから取得します。
opt <- c(RSS.table[
as.character(opt[1]),
i
], opt)
}
}
# 最適なブレイクポイント位置のベクトルoptを返します。名前属性は削除します。
names(opt) <- NULL
return(opt)
}
# extract.breaks関数を用いて、RSS.tableから最適なブレイクポイントoptを抽出します。
opt <- extract.breaks(RSS.table, breaks)
# データが時系列データtsかどうかを判定します。
if (is.ts(data)) {
# データが時系列データであり、かつデータ行数がn(観測数)と一致する場合、
if (NROW(data) == n) {
# データの時系列属性(tsp)をdatatspに格納します。
datatsp <- tsp(data)
} # データが時系列データであるが、行数がnと一致しない場合、
else {
# デフォルトの時系列属性を設定します(開始時点1/n、終了時点1、観測数n)。
datatsp <- c(1 / n, 1, n)
}
}
# データが時系列データでない場合
else {
# formulaの環境を取得します。
env <- environment(formula)
# data引数が欠損している場合、環境envをデータとして使用します。
if (missing(data)) {
data <- env
}
# モデル項modeltermsから応答変数の変数名を取得し、data環境内で評価して元の応答変数orig.yを取得します。
orig.y <- eval(
attr(modelterms, "variables")[[2]], data,
env
)
# 元の応答変数orig.yが時系列データであり、かつ行数がn(観測数)と一致する場合、
if (is.ts(orig.y) & (NROW(orig.y) == n)) {
# 元の応答変数の時系列属性(tsp)をdatatspに格納します。
datatsp <- tsp(orig.y)
} # 元の応答変数orig.yが時系列データでないか、または行数がnと一致しない場合、
else {
# デフォルトの時系列属性を設定します(開始時点1/n、終了時点1、観測数n)。
datatsp <- c(1 / n, 1, n)
}
}
# RVALリストに、breakpointsfullおよびbreakpointsクラスの属性を持たせたリストを作成し、結果を格納します。
RVAL <- list(
breakpoints = opt, RSS.table = RSS.table, RSS.triang = RSS.triang,
RSS = RSS, extract.breaks = extract.breaks, extend.RSS.table = extend.RSS.table,
nobs = n, nreg = k, y = y, X = X, call = match.call(),
datatsp = datatsp
)
class(RVAL) <- c("breakpointsfull", "breakpoints")
# breakpointsメソッドを適用して、RVALオブジェクトからブレイクポイントを抽出し、RVAL$breakpointsに再代入します。
RVAL$breakpoints <- breakpoints(RVAL)$breakpoints
# 結果リストRVALを返します。
return(RVAL)
}上記コードの通り、本関数は動的計画法を利用して、引数h から ceiling(n / h) - 2 として求めた、または breaks で指定した構造変化点数を上限として、構造変化点数毎に可能な全ての構造変化点の組み合わせについて、線形回帰 の結果から 残差平方和(RSS) を算出し、最小の RSS を取る構造変化点の組み合わせを構造変化点数毎に求め、さらに、関数 summary.breakpointsfull により構造変化点数毎の 情報量基準BIC から同基準が最小となる構造変化点数とその構造変化点を出力します。
以下は関数 summary.breakpointsfull のコードです。
getAnywhere(summary.breakpointsfull)A single object matching 'summary.breakpointsfull' was found
It was found in the following places
registered S3 method for summary from namespace strucchange
namespace:strucchange
with value
function (object, breaks = NULL, sort = NULL, format.times = NULL,
...)
{
if (is.null(format.times))
format.times <- ((object$datatsp[3] > 1) & (object$datatsp[3] <
object$nobs))
if (is.null(breaks))
breaks <- ncol(object$RSS.table)/2
n <- object$nobs
RSS <- c(object$RSS(1, n), rep(NA, breaks))
BIC <- c(n * (log(RSS[1]) + 1 - log(n) + log(2 * pi)) + log(n) *
(object$nreg + 1), rep(NA, breaks))
names(RSS) <- as.character(0:breaks)
bp <- breakpoints(object, breaks = breaks)
bd <- breakdates(bp, format.times = format.times)
RSS[breaks + 1] <- bp$RSS
BIC[breaks + 1] <- AIC(bp, k = log(n))
bp <- bp$breakpoints
if (breaks > 1) {
for (m in (breaks - 1):1) {
bp <- rbind(NA, bp)
bd <- rbind(NA, bd)
bpm <- breakpoints(object, breaks = m)
if (is.null(sort) || identical(sort, TRUE)) {
pos <- apply(outer(bpm$breakpoints, bp[nrow(bp),
], FUN = function(x, y) abs(x - y)), 1, which.min)
if (length(pos) > length(unique(pos))) {
if (!is.null(sort))
warning("sorting not possible", call. = FALSE)
sort <- FALSE
}
else {
sort <- TRUE
}
}
if (!sort)
pos <- 1:m
bp[1, pos] <- bpm$breakpoints
bd[1, pos] <- breakdates(bpm, format.times = format.times)
RSS[m + 1] <- bpm$RSS
BIC[m + 1] <- AIC(bpm, k = log(n))
}
}
else {
bp <- as.matrix(bp)
bd <- as.matrix(bd)
}
rownames(bp) <- as.character(1:breaks)
colnames(bp) <- rep("", breaks)
rownames(bd) <- as.character(1:breaks)
colnames(bd) <- rep("", breaks)
RSS <- rbind(RSS, BIC)
rownames(RSS) <- c("RSS", "BIC")
RVAL <- list(breakpoints = bp, breakdates = bd, RSS = RSS,
call = object$call)
class(RVAL) <- "summary.breakpointsfull"
return(RVAL)
}
<bytecode: 0x000001d3ec8add60>
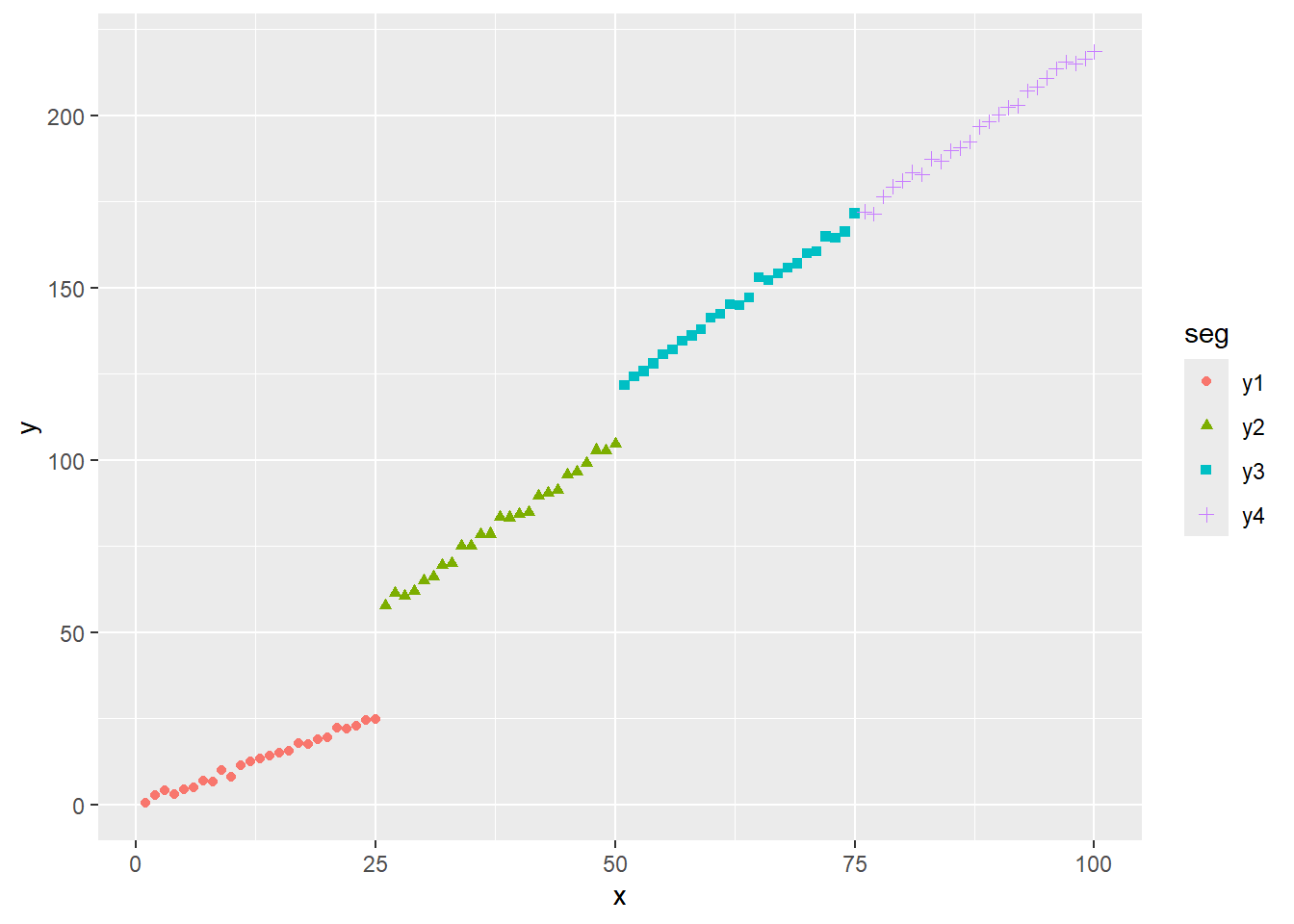
<environment: namespace:strucchange>始めにサンプルデータを作成します。サンプルサイズは100点。セグメントは計4つ(y1、y2、y3、y4)。切片、傾きいずれか一つでも異なるのは25点目(y1とy2)と50点目(y2とy3)の2点です。
library(dplyr)
library(ggplot2)
seed <- 20250309
set.seed(seed)
fun_y <- function(x, beta, seg) {
n <- length(x)
y <- (beta %*% t(data.frame(x, 1)) + rnorm(n)) %>% as.vector() # 残差の平均値と分散は同一
return(data.frame(x, y, seg))
}
y1 <- fun_y(x = 1:25, beta = c(1, 0), seg = "y1") # y2、y3、y4とは切片、傾きそして残差が異なる
y2 <- fun_y(x = 26:50, beta = c(2, 5), seg = "y2") # y3、y4と切片と残差が異なる
y3 <- fun_y(x = 51:75, beta = c(2, 20), seg = "y3") # y4と係数は同一、残差のみ異なる
y4 <- fun_y(x = 76:100, beta = c(2, 20), seg = "y4")
sampledf <- Reduce(function(x, y) rbind(x, y), list(y1, y2, y3, y4))
sampledf %>% ggplot(mapping = aes(x = x, y = y, colour = seg, shape = seg)) +
geom_point()引数h に1未満の数値を指定した場合は floor(n * h) が最小セグメントサイズとなります。デフォルトは0.15ですので本サンプルでは 100 × 0.15 = 15ポイント が最小セグメントサイズになります。
result <- strucchange::breakpoints(sampledf$y ~ sampledf$x)
result
Optimal 3-segment partition:
Call:
breakpoints.formula(formula = sampledf$y ~ sampledf$x)
Breakpoints at observation number:
25 50
Corresponding to breakdates:
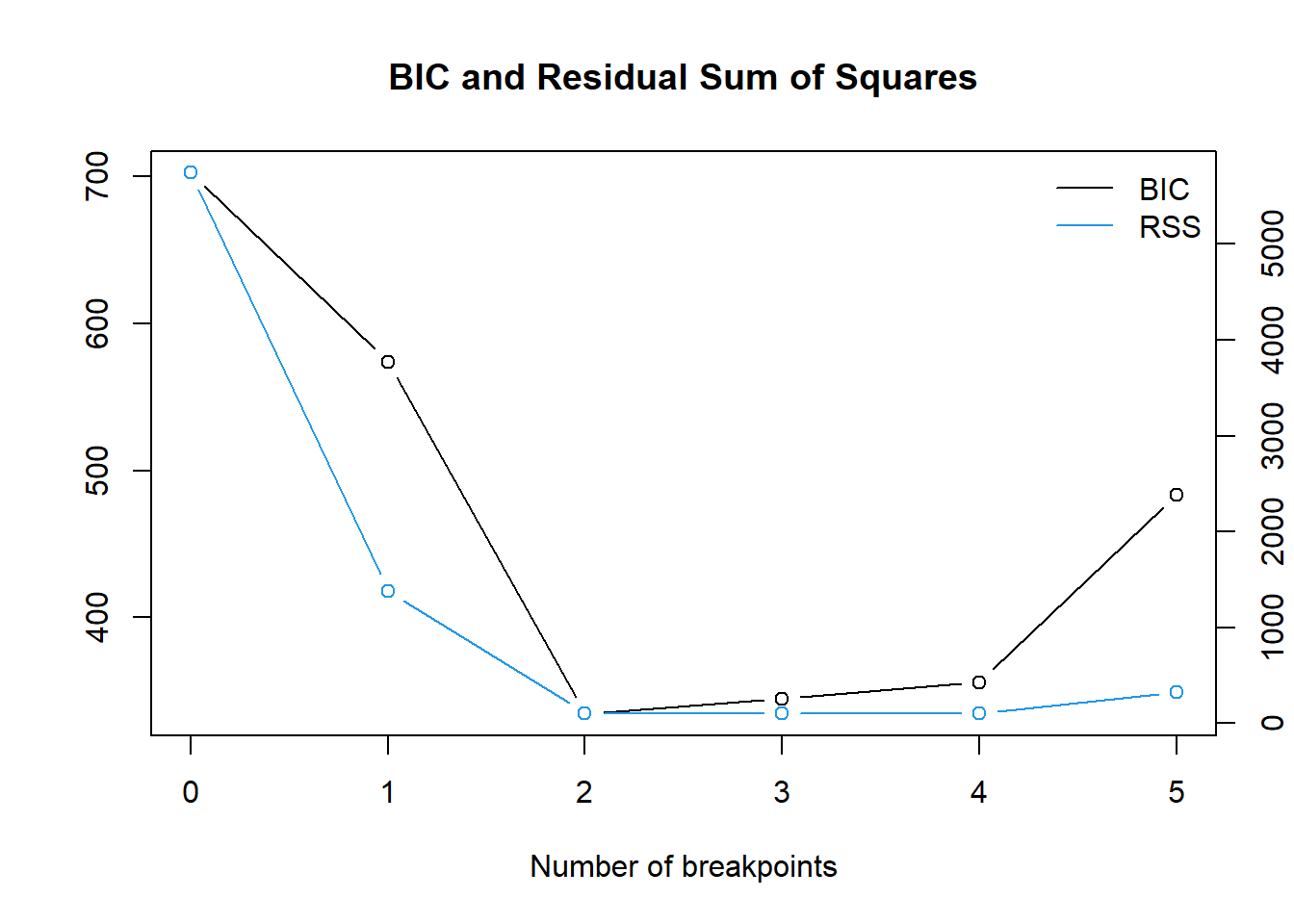
0.25 0.5 summary(result)
plot(result)
Optimal (m+1)-segment partition:
Call:
breakpoints.formula(formula = sampledf$y ~ sampledf$x)
Breakpoints at observation number:
m = 1 25
m = 2 25 50
m = 3 25 50 77
m = 4 25 50 67 83
m = 5 25 40 55 70 85
Corresponding to breakdates:
m = 1 0.25
m = 2 0.25 0.5
m = 3 0.25 0.5 0.77
m = 4 0.25 0.5 0.67 0.83
m = 5 0.25 0.4 0.55 0.7 0.85
Fit:
m 0 1 2 3 4 5
RSS 5743.5 1382.6 109.6 105.8 102.9 321.6
BIC 702.7 574.1 334.4 344.6 355.7 483.5情報量基準BIC が最も小さいのは「構造変化点は2点(m=2)」かつ「25点目と50点目の組み合わせ」とした場合。RSS が最も小さいのは「構造変化点は4点(m=4)」かつ「25点目、50点目、67点目、83点目の組み合わせ」とした場合、との結果になりました。
本関数単独自体では RSS を利用したF検定の結果(p値)により帰無仮説(例 H0:構造変化なし)を判断する関数ではありませんので、出力された 情報量基準BIC で判断しますと、サンプルデータで設定した2つの構造変化点が抽出できていることになります。
本関数の注意点としては、構造変化点を超えた 引数h としますと、適切な結果が得られません。極端な例として例えば h = 0.4、100 × 0.4 = 40 としますと 40 > 25 であるため以下の通りの結果が出力されます。
strucchange::breakpoints(sampledf$y ~ sampledf$x, h = 0.4)
Optimal 2-segment partition:
Call:
breakpoints.formula(formula = sampledf$y ~ sampledf$x, h = 0.4)
Breakpoints at observation number:
50
Corresponding to breakdates:
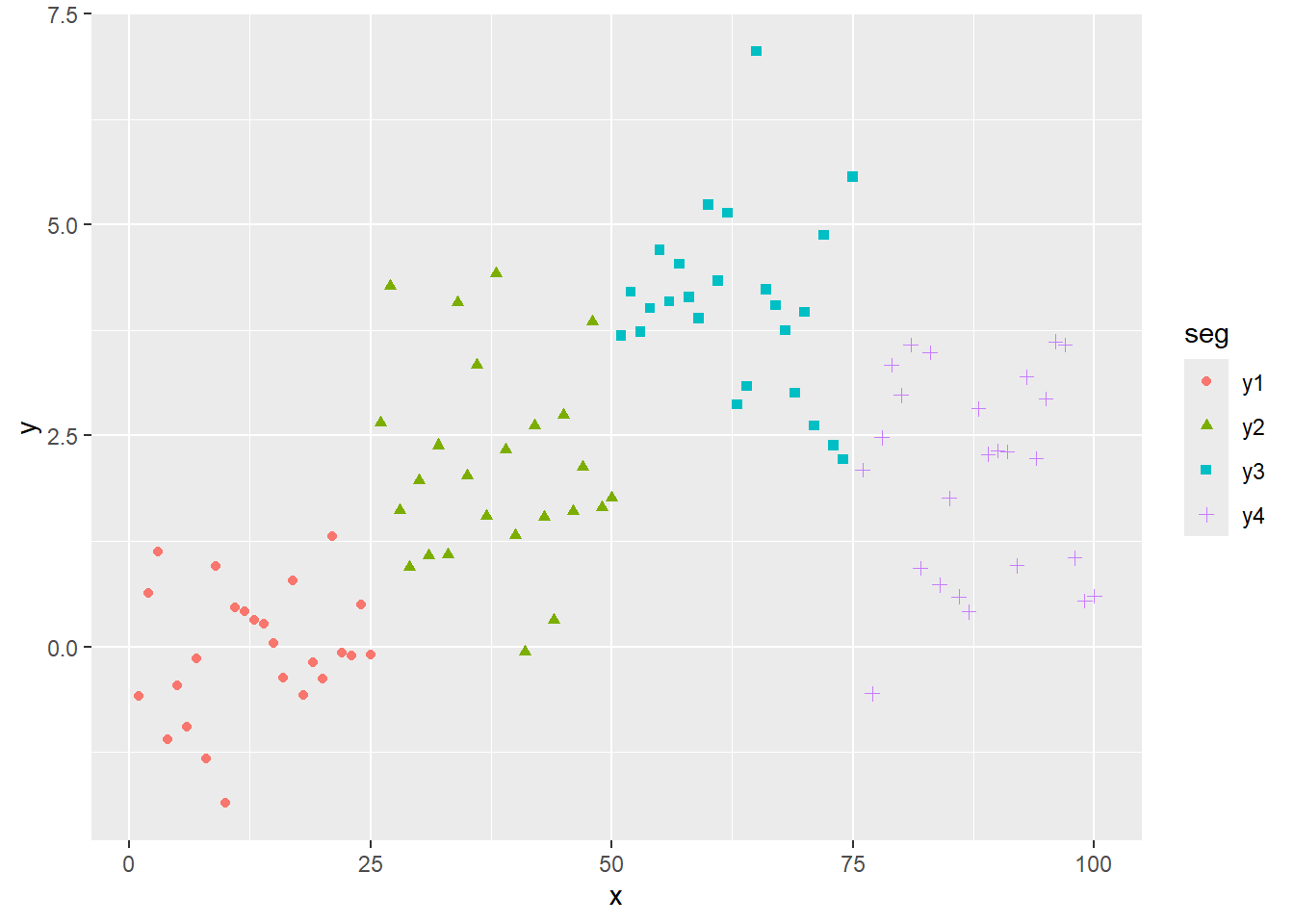
0.5 続いて傾きの無い、平均値のみのサンプルデータを作成します。構造変化点は25点目、50点目、75点目の3点とします。
set.seed(seed)
fun_y <- function(x, mean_value, seg) {
n <- length(x)
y <- rnorm(n = n, mean = mean_value, sd = 1)
return(data.frame(x, y, seg))
}
y1 <- fun_y(x = 1:25, mean_value = 0, seg = "y1")
y2 <- fun_y(x = 26:50, mean_value = 2, seg = "y2")
y3 <- fun_y(x = 51:75, mean_value = 4, seg = "y3")
y4 <- fun_y(x = 76:100, mean_value = 2, seg = "y4")
sampledf <- Reduce(function(x, y) rbind(x, y), list(y1, y2, y3, y4))
sampledf %>% ggplot(mapping = aes(x = x, y = y, colour = seg, shape = seg)) +
geom_point()切片のみ のモデルとして構造変化点数毎の最小 RSS と 情報量基準BIC の組み合わせを求めます。
result <- strucchange::breakpoints(sampledf$y ~ 1)
result
Optimal 4-segment partition:
Call:
breakpoints.formula(formula = sampledf$y ~ 1)
Breakpoints at observation number:
25 50 75
Corresponding to breakdates:
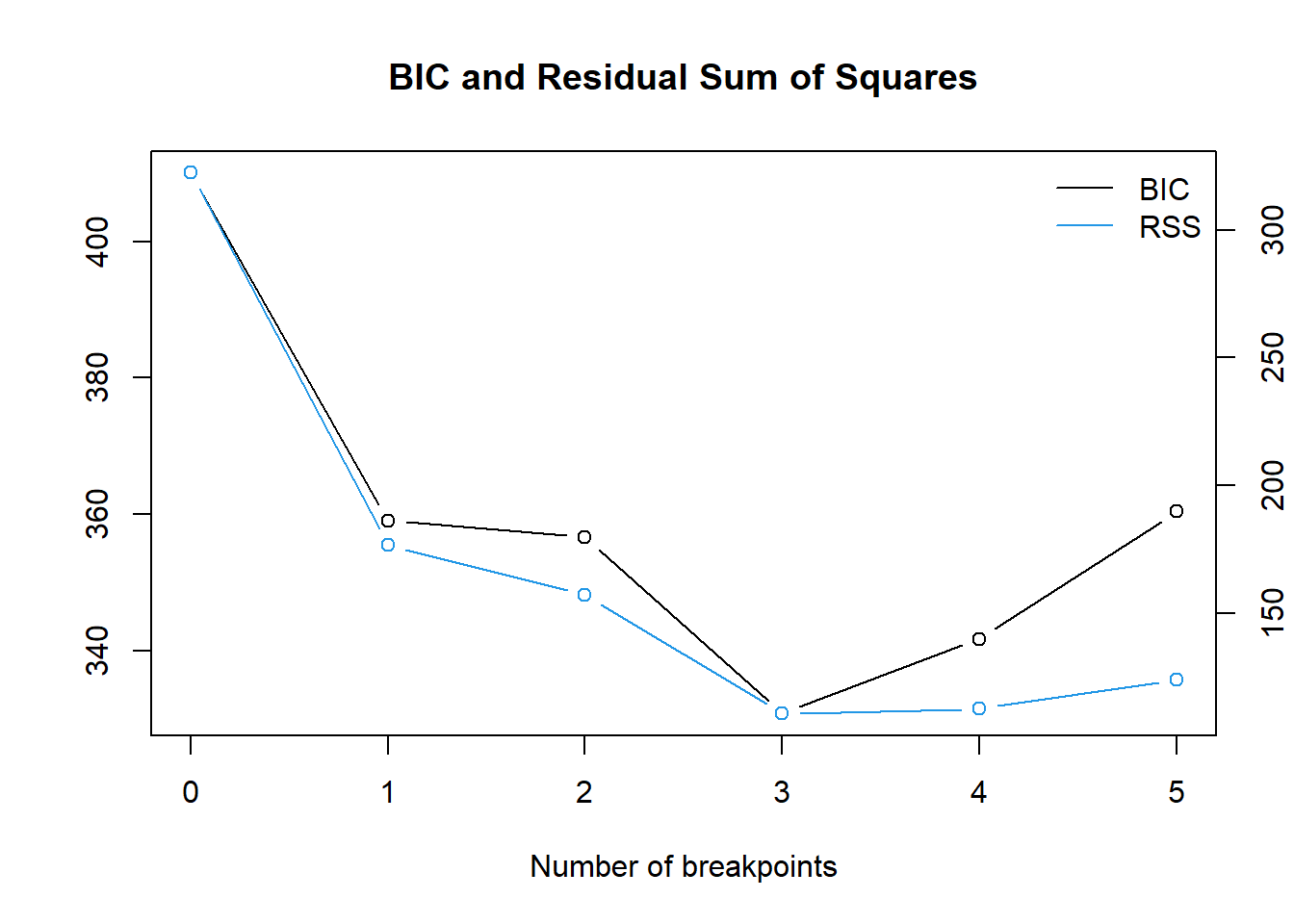
0.25 0.5 0.75 summary(result)
plot(result)
Optimal (m+1)-segment partition:
Call:
breakpoints.formula(formula = sampledf$y ~ 1)
Breakpoints at observation number:
m = 1 25
m = 2 25 75
m = 3 25 50 75
m = 4 25 50 68 83
m = 5 20 35 50 68 83
Corresponding to breakdates:
m = 1 0.25
m = 2 0.25 0.75
m = 3 0.25 0.5 0.75
m = 4 0.25 0.5 0.68 0.83
m = 5 0.2 0.35 0.5 0.68 0.83
Fit:
m 0 1 2 3 4 5
RSS 322.4 176.6 157.2 110.7 112.7 123.8
BIC 410.1 359.1 356.6 330.8 341.8 360.4「構造変化点は3点(m=3)」かつ「25点目、50点目、75点目の組み合わせ」とした場合に RSS も 情報量基準BIC も最小となりました。
以上です。