Rでロバスト線形回帰 残差尺度(MADとHuber)の比較

ロバスト線形回帰を扱うRの関数 rlm {MASS} について、引数 method を M推定 とした場合における、引数 scale.est の2つの選択肢、MAD(中央絶対偏差(Median Absolute Deviation)) と Huber それぞれの結果をシミュレーションで比較します。

本ポストは以下の資料を参照引用しています。

前述の scale.est はロバスト線形回帰における 残差尺度(スケール) を指定する引数です。

M推定 では回帰係数 \(\beta\) を次の目的関数を最小化することで推定します。

\[\underset{\beta}{\textrm{min}}\displaystyle\sum_{i=1}^n\rho\left(\dfrac{y_i-x_i^{T}\beta}{\sigma}\right)\] ここで、\(\rho\) は損失関数、\(\sigma\) は残差の残差尺度パラメータ。

scale.est method of scale estimation: re-scaled MAD of the residuals (default) or Huber’s proposal 2 (which can be selected by either “Huber” or “proposal 2”).
出所:https://cran.r-project.org/web/packages/MASS/MASS.pdf

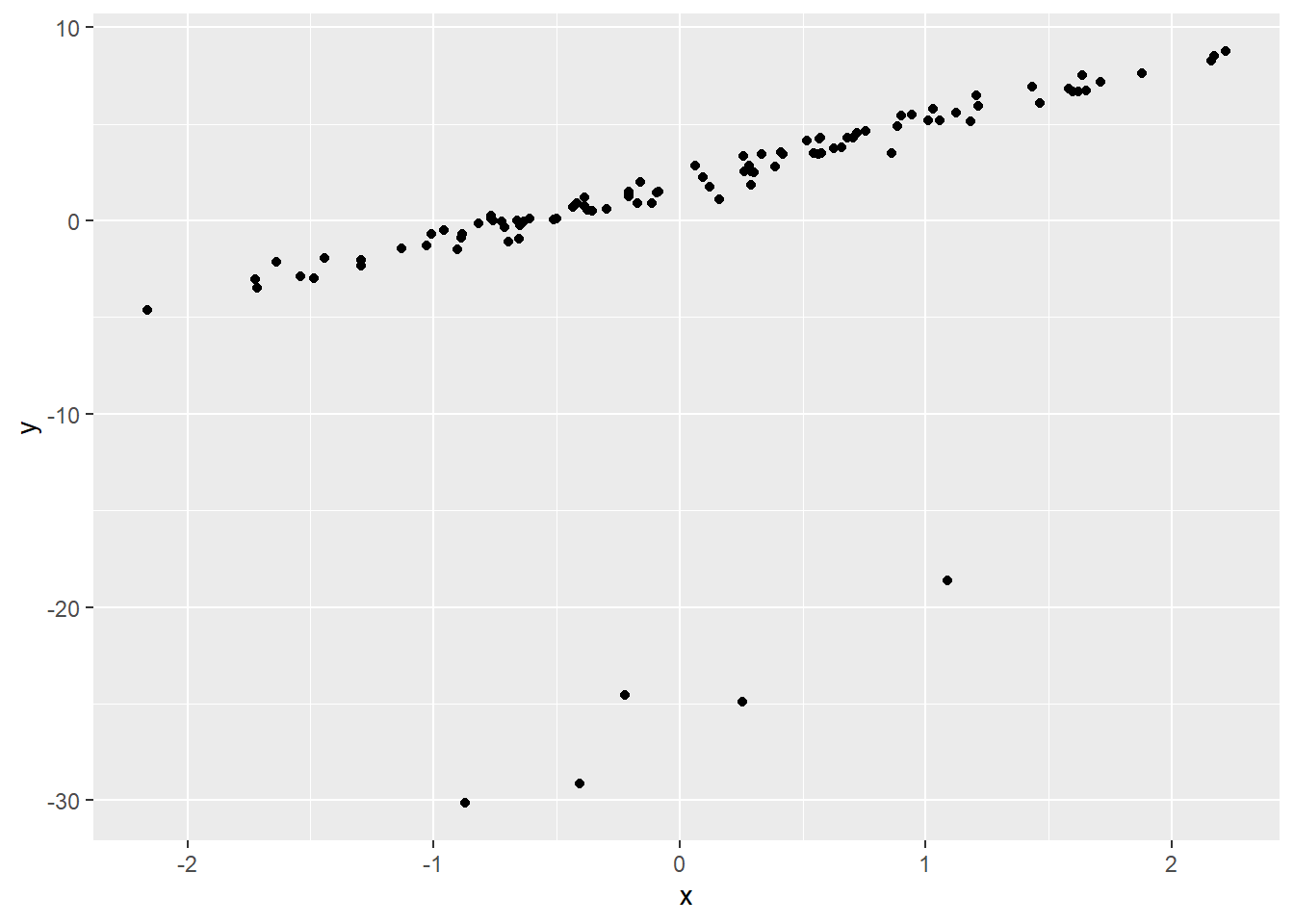
始めに外れ値のあるサンプルデータを生成する関数を作成します。

なお、外れ値は全て「意図的に大きな外れ」とし、かつ回帰直線を「下方向に引っ張る」値とします。

fun_sampledata <- function(seed, n, nout) {
  set.seed(seed)

  # 真のモデル: y = 2 + 3x + ε
  x <- rnorm(n)
  y_true <- 2 + 3 * x
  y <- y_true + rnorm(n, sd = 0.5)

  # 外れ値追加
  id_out <- sample(x = seq(n), size = nout, replace = F)
  y[id_out] <- y_true[id_out] + runif(n = nout, min = -30, max = -20)

  data <- data.frame(x = x, y = y)
  return(data)
}

サンプルサイズは100点。うち5点(全体の5%)を外れ値としたサンプルです。

library(dplyr)
seed <- 20250325
n <- 100
nout <- 5 # 外れ値数
data <- fun_sampledata(seed = seed, n = n, nout = nout)
glimpse(data)

Rows: 100
Columns: 2
$ x <dbl> 0.41244091, -0.29726921, 0.75426413, -1.02650381, -0.90249637, -0.37…
$ y <dbl> 3.51826312, 0.61542828, 4.63224788, -1.29074946, -1.50497772, 0.5556…

外れ度合い をチャートで確認します。

library(ggplot2)
ggplot(data = data, mapping = aes(x = x, y = y)) +
  geom_point()

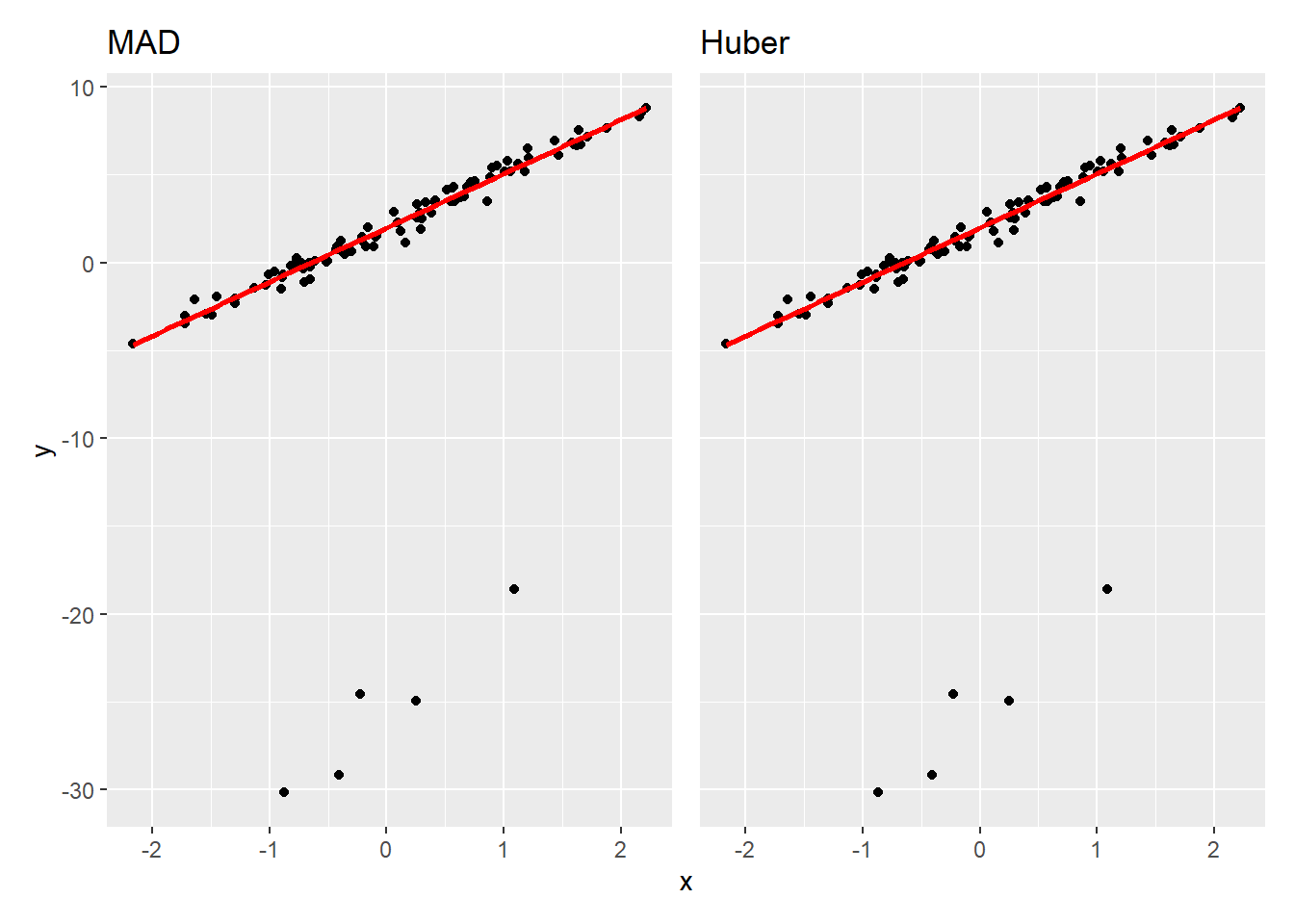
作成したサンプルデータについて、残差尺度 を MAD および Huber とした結果をチャートで比較します。

library(MASS)
library(patchwork)
g_MAD <- ggplot(data = data, mapping = aes(x = x, y = y)) +
  geom_point() +
  geom_smooth(method = "rlm", se = F, color = "red", method.args = list(method = "M", psi = psi.bisquare, scale.est = "MAD")) +
  labs(title = "MAD")
g_Huber <- ggplot(data = data, mapping = aes(x = x, y = y)) +
  geom_point() +
  geom_smooth(method = "rlm", se = F, color = "red", method.args = list(method = "M", psi = psi.bisquare, scale.est = "Huber")) +
  labs(title = "Huber")
g_MAD + g_Huber + plot_layout(axes = "collect")

目視では MAD と Huber に差はほぼ見られませんが、

list(MAD = rlm(data$y ~ data$x, method = "M", psi = psi.bisquare, scale.est = "MAD"), Huber = rlm(data$y ~ data$x, method = "M", psi = psi.bisquare, scale.est = "Huber"))

$MAD
Call:
rlm(formula = data$y ~ data$x, psi = psi.bisquare, scale.est = "MAD", 
    method = "M")
Converged in 4 iterations

Coefficients:
(Intercept)      data$x 
   1.974910    3.075421 

Degrees of freedom: 100 total; 98 residual
Scale estimate: 0.484 

$Huber
Call:
rlm(formula = data$y ~ data$x, psi = psi.bisquare, scale.est = "Huber", 
    method = "M")
Converged in 7 iterations

Coefficients:
(Intercept)      data$x 
   1.975536    3.075422 

Degrees of freedom: 100 total; 98 residual
Scale estimate: 0.471

実際には切片、傾き(僅か)、そして 残差尺度 全てに差が生じています

それでは300試行のシミュレーションにより、残差尺度を MAD および Huber とした場合それぞれのロバスト線形回帰の係数(切片と傾き)と 残差尺度 を比較します。

fun_simulation <- function(iter, n, nout) {
  formulatxt <- sampledf$y~sampledf$x
  method <- "M"
  psi <- psi.bisquare
  maxit <- 100
  for (iii in seq(iter)) {
    sampledf <- fun_sampledata(seed = iii, n = n, nout = nout)
    # 係数の抽出
    result.rlm.m.mad <-
      rlm(formulatxt,
        scale.est = "MAD",
        method = method,
        psi = psi,
        maxit = maxit
      )$coef
    result.rlm.m.huber <-
      rlm(formulatxt,
        scale.est = "Huber",
        method = method,
        psi = psi,
        maxit = maxit
      )$coef
    resultdf0 <- rbind(result.rlm.m.mad, result.rlm.m.huber) %>%
      t() %>%
      data.frame(check.names = F) %>%
      {
        .$itr <- iii
        .
      }
    if (iii == 1) {
      resultdf_coef <- resultdf0
    } else {
      resultdf_coef <- rbind(resultdf_coef, resultdf0)
    }
    # スケールの抽出
    result.rlm.m.mad <-
      rlm(formulatxt,
        scale.est = "MAD",
        method = method,
        psi = psi,
        maxit = maxit
      )$s
    result.rlm.m.huber <-
      rlm(formulatxt,
        scale.est = "Huber",
        method = method,
        psi = psi,
        maxit = maxit
      )$s
    resultdf0 <- data.frame(result.rlm.m.mad, result.rlm.m.huber, itr = iii)
    if (iii == 1) {
      resultdf_scale <- resultdf0
    } else {
      resultdf_scale <- rbind(resultdf_scale, resultdf0)
    }
  }
  # 切片
  tidydf <- resultdf_coef %>%
    row.names() %>%
    grep("Intercept", .) %>%
    resultdf_coef[., ] %>%
    {
      tidyr::gather(., , , colnames(.)[-3])
    }
  g_coef_intercept <- tidydf %>% ggplot(mapping = aes(x = "", y = value)) +
    geom_boxplot() +
    geom_jitter() +
    facet_wrap(. ~ key, scales = "free_y") +
    theme(axis.title = element_blank()) +
    labs(title = "Intercept")
  # 傾き
  tidydf <- resultdf_coef %>%
    row.names() %>%
    grep("sampledf", .) %>%
    resultdf_coef[., ] %>%
    {
      tidyr::gather(., , , colnames(.)[-3])
    }
  g_coef_slope <- tidydf %>% ggplot(mapping = aes(x = "", y = value)) +
    geom_boxplot() +
    geom_jitter() +
    facet_wrap(. ~ key, scales = "free_y") +
    theme(axis.title = element_blank()) +
    labs(title = "Slope")
  # スケール
  tidydf <- resultdf_scale %>%
    {
      tidyr::gather(., , , colnames(.)[-3])
    }
  g_scale <- tidydf %>% ggplot(mapping = aes(x = "", y = value)) +
    geom_boxplot() +
    geom_jitter() +
    facet_wrap(. ~ key, scales = "free_y") +
    theme(axis.title = element_blank()) +
    labs(title = "Scale")
  g_coef_intercept + g_coef_slope + g_scale + plot_layout(nrow = 3)
}

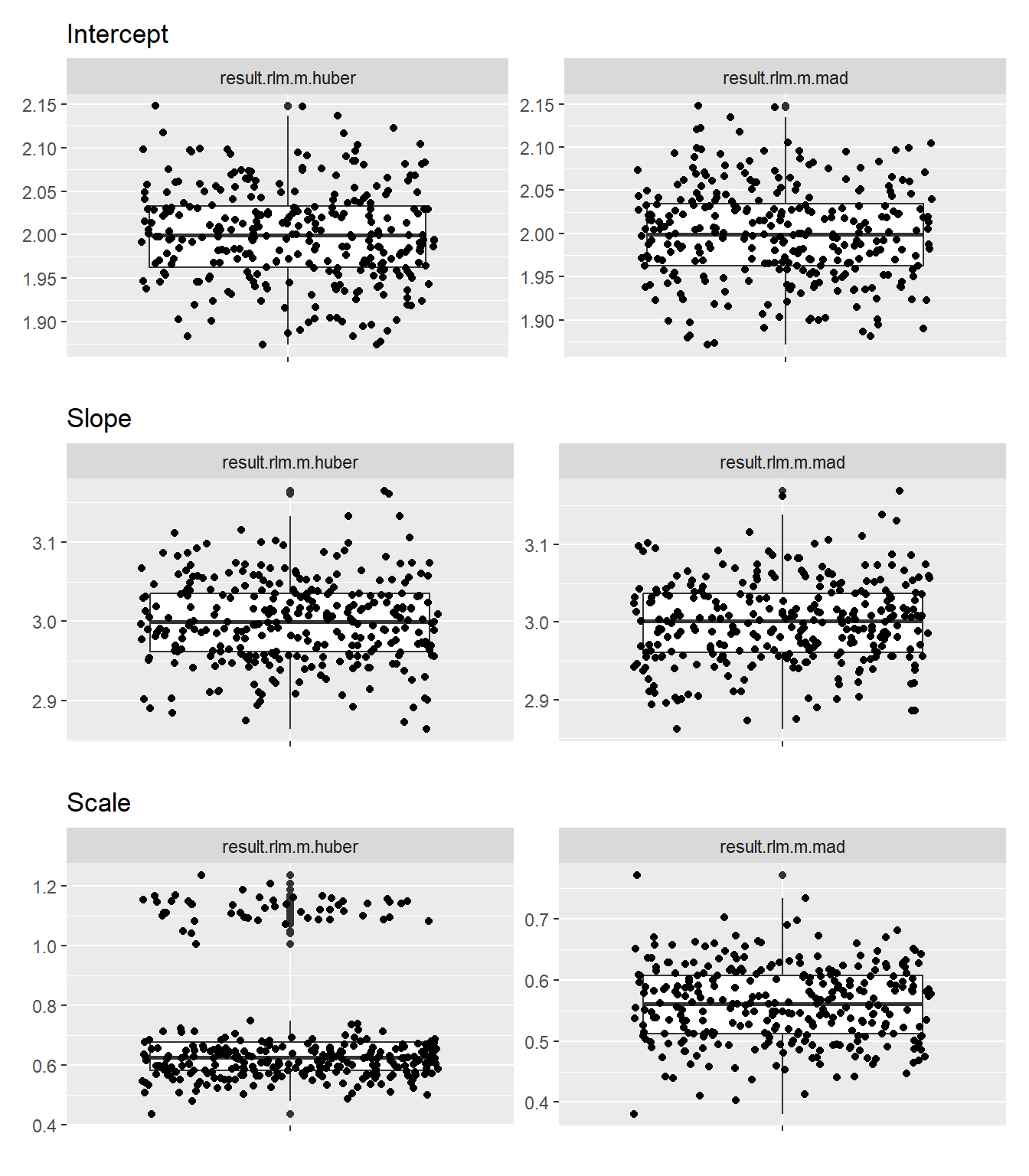
始めに外れ値を全体の10%とした場合を比較します。

fun_simulation(iter = 300, n = 100, nout = 10)

残差尺度 には違いが見られますが、切片と傾きは中央値および分散とも MAD と Huber とで、ほぼ同じ結果になりました。

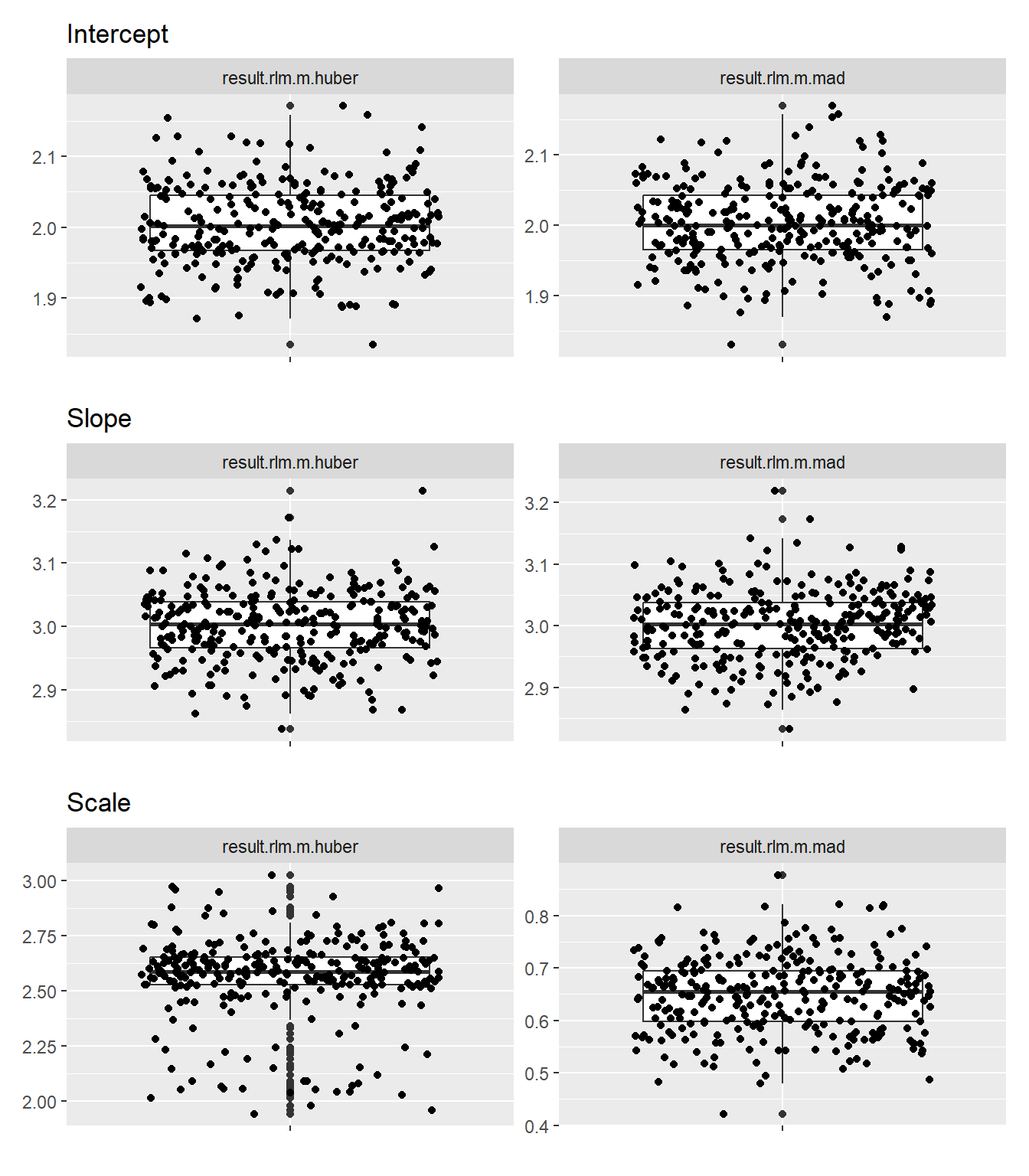
続いて外れ値を全体の30%にした場合です。

fun_simulation(iter = 300, n = 100, nout = 20)

残差尺度 の違いはより大きくなりましたが、それでも切片と傾きは中央値および分散とも MAD と Huber とで、ほぼ同じ結果になりました。

以上です。