Rを利用して 高速フーリエ変換 を試みます。
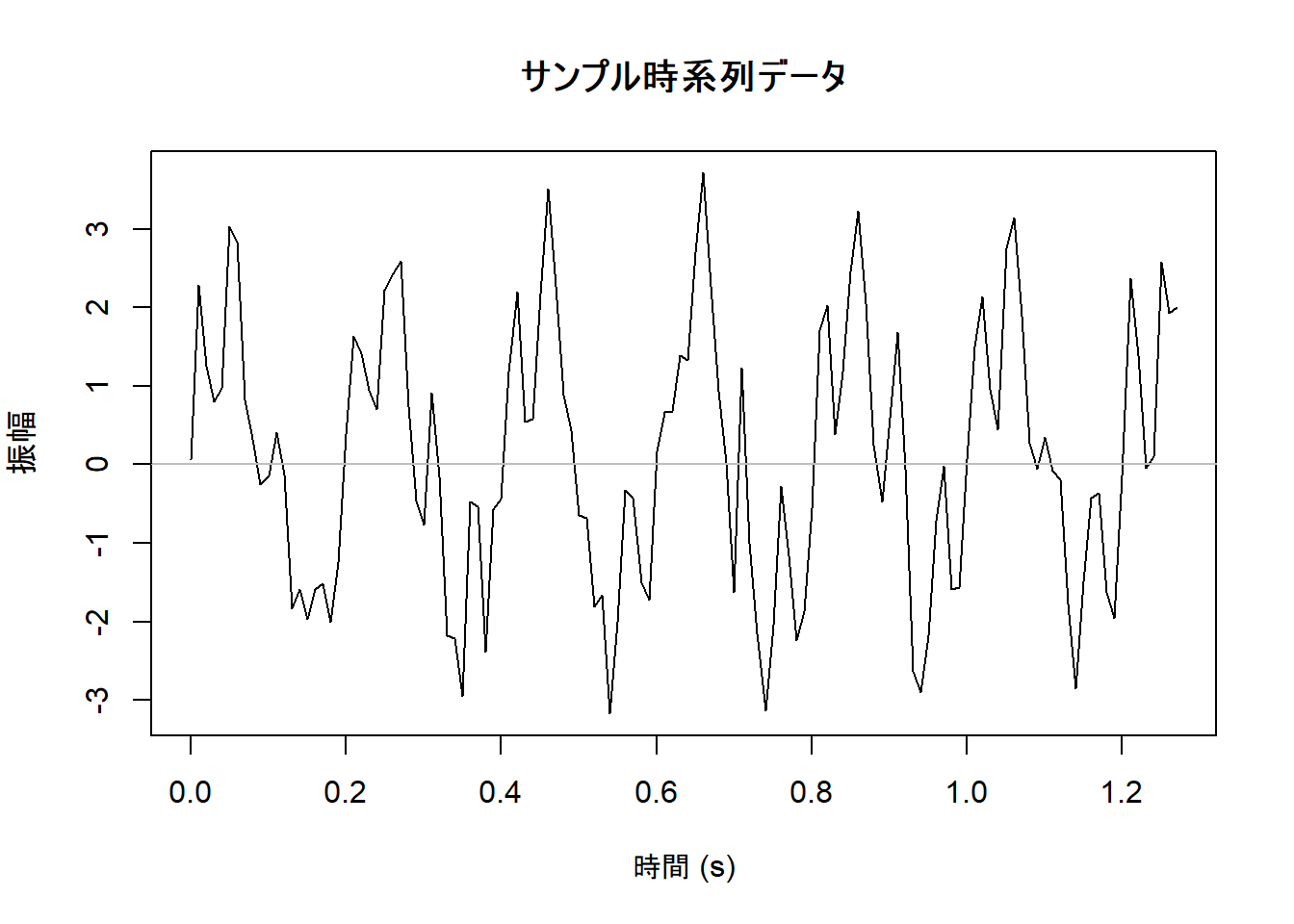
始めに2つの正弦波(5Hzと20Hz)を重ね合わせたサンプル時系列データを作成します。
seed <- 20250531
set.seed(seed)
# サンプルデータのパラメータ
N <- 128 # データ点数 (2のべき乗とする)
Fs <- 100 # サンプリング周波数 (Hz)
t <- (0:(N - 1)) / Fs # 時間ベクトル (0から (N-1)/Fs まで)
# 信号成分
f1 <- 5 # 第1の周波数 (Hz)
A1 <- 2 # 第1の振幅
f2 <- 20 # 第2の周波数 (Hz)
A2 <- 1 # 第2の振幅
signal <- A1 * sin(2 * pi * f1 * t) + A2 * sin(2 * pi * f2 * t)
# ノイズ成分
noise_amplitude <- 0.5
noise <- noise_amplitude * rnorm(N) # 正規分布に従うノイズ
# ノイズを加えた信号
data_time_series <- signal + noise
# 時系列データのプロット
plot(t, data_time_series,
type = "l",
xlab = "時間 (s)", ylab = "振幅",
main = "サンプル時系列データ"
)
abline(h = 0, col = "grey")続いて 高速フーリエ変換 のための関数を Cooley-Tukeyアルゴリズム により作成します。
fft_recursive <- function(x) {
N <- length(x)
# 基底ケース: N=1ならそのまま返す
if (N <= 1) {
return(as.complex(x))
}
# 偶数番目の要素と奇数番目の要素に分割
even_indices <- seq(1, N, by = 2)
odd_indices <- seq(2, N, by = 2)
x_even <- x[even_indices]
x_odd <- x[odd_indices]
# 再帰的にFFTを計算
X_even <- fft_recursive(x_even)
X_odd <- fft_recursive(x_odd)
# 結果を結合(バタフライ演算)
X <- complex(length.out = N) # 結果を格納する複素数ベクトル
for (k in 0:(N / 2 - 1)) {
# 回転因子(複素数)
twiddle_factor <- exp(-2 * pi * 1i * k / N)
# Rのインデックスは1から始まる
X[k + 1] <- X_even[k + 1] + twiddle_factor * X_odd[k + 1]
X[k + N / 2 + 1] <- X_even[k + 1] - twiddle_factor * X_odd[k + 1]
}
return(X)
}サンプル時系列データを 高速フーリエ変換 にかけます。
fft_result <- fft_recursive(x = data_time_series)
head(fft_result)[1] 16.72316+0.0000000i 12.69468+2.9159884i 8.94039-0.2680589i
[4] 12.50588-3.5751752i 20.75956-4.2024217i 21.97059-7.1845007iFFTの結果の最初の要素 (fft_result[1]) はDC成分(周波数0Hz)です。
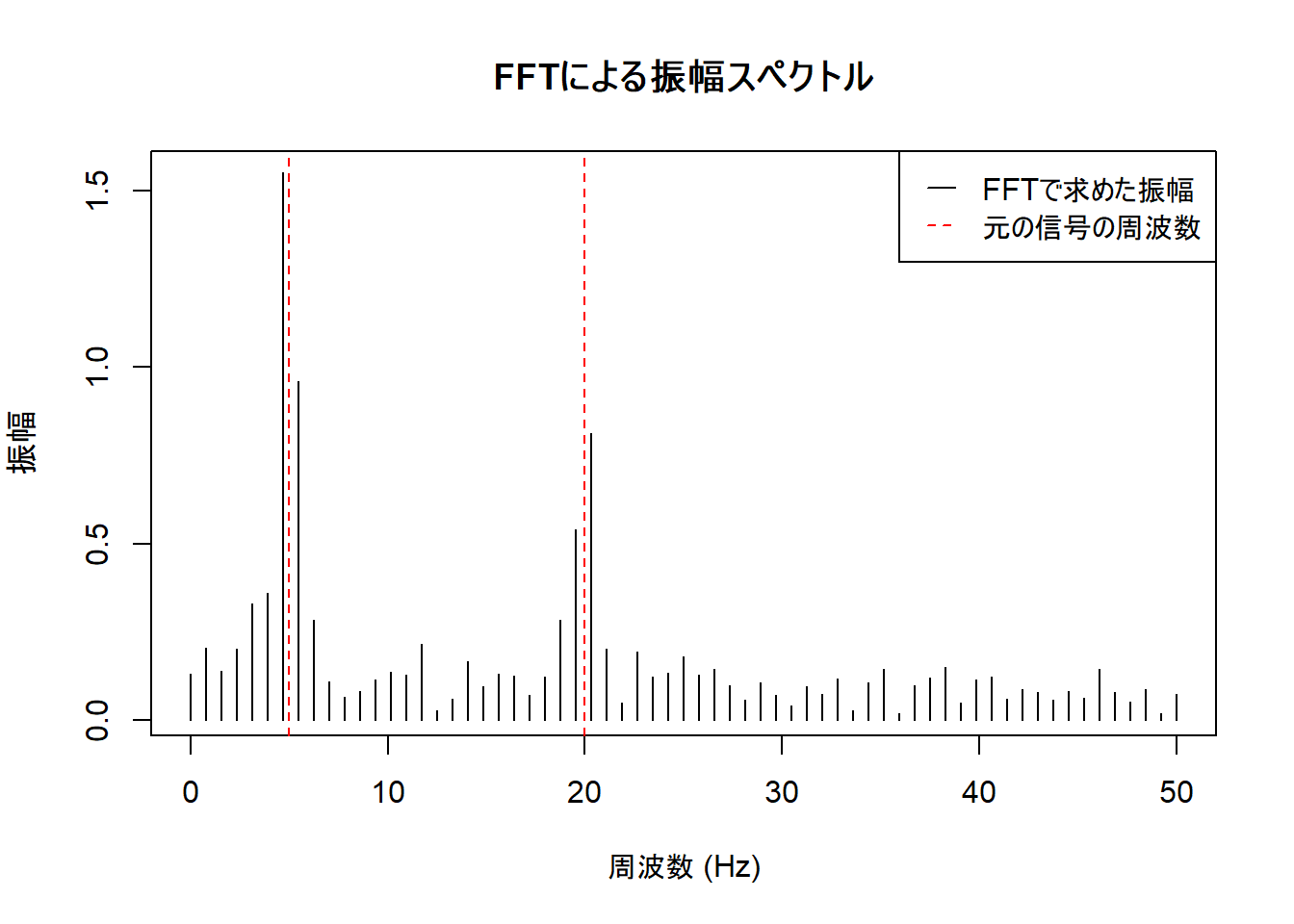
振幅スペクトルをプロットします。
# DC成分 + 正の周波数成分の数
num_unique_pts <- ceiling((N + 1) / 2)
# 振幅スペクトル(各周波数成分の強さ)
# Mod() で複素数の絶対値(振幅)を取得
amplitudes <- Mod(fft_result)
# 片側スペクトルの振幅を取得
amplitudes_onesided <- amplitudes[1:num_unique_pts]
# 振幅の正規化
# DC成分 (0 Hz) は N で割る
amplitudes_scaled <- amplitudes_onesided / N
# 他の周波数成分は N で割ってから2倍する
# 負の周波数成分を正の周波数成分に加算するため
amplitudes_scaled[2:(num_unique_pts - 1)] <- 2 * amplitudes_scaled[2:(num_unique_pts - 1)]
# 周波数の作成
# FFTの結果のk番目の要素は (k-1)*Fs/N Hz の周波数に対応
# ナイキスト周波数 Fs/2 までの片側スペクトルを見る
frequencies <- (0:(num_unique_pts - 1)) * Fs / N
# 振幅スペクトルのプロット
plot(frequencies, amplitudes_scaled,
type = "h",
xlab = "周波数 (Hz)", ylab = "振幅",
main = "FFTによる振幅スペクトル",
xlim = c(0, Fs / 2)
)
abline(v = c(f1, f2), col = "red", lty = 2)
legend("topright", legend = c("FFTで求めた振幅", "元の信号の周波数"), col = c("black", "red"), lty = c(1, 2), lwd = c(1, 1), seg.len = 1)サンプル時系列データの信号成分(第1の周波数 5(Hz)、第2の周波数 20(Hz)) が抽出できており、それぞれ設定した振幅に近い結果が確認できます(ノイズを加算していますので一致はしません)。
Rの関数 fft {stats} を利用して 高速フーリエ変換 にかけ、結果が一致しているか確認します。
fft_result_by_fft_stats <- fft(data_time_series)
amplitudes_by_fft_stats <- Mod(fft_result_by_fft_stats)
amplitudes_onesided_by_fft_stats <- amplitudes_by_fft_stats[1:num_unique_pts]
amplitudes_scaled_by_fft_stats <- amplitudes_onesided_by_fft_stats / N
amplitudes_scaled_by_fft_stats[2:(num_unique_pts - 1)] <- 2 * amplitudes_scaled_by_fft_stats[2:(num_unique_pts - 1)]
all.equal(amplitudes_scaled, amplitudes_scaled_by_fft_stats)[1] TRUE一致しています。
最後に参考として位相スペクトルをプロットします。
phases_by_fft_stats <- Arg(fft_result_by_fft_stats[1:num_unique_pts]) # Arg()で複素数の偏角(位相)を取得
plot(frequencies, phases_by_fft_stats,
type = "h",
xlab = "周波数 (Hz)", ylab = "位相 (ラジアン)",
main = "FFTによる位相スペクトル",
xlim = c(0, Fs / 2)
)以上です。