Rによる 時系列データ の 季節成分 と トレンド成分 への分解を試みます。
本ポストでは、Rの関数 stl を利用して分解します。
関数 stl は Seasonal Decomposition of Time Series by Loess のとおり、Loess を用いて時系列データを 季節成分、トレンド成分、残差成分 に分解します。


始めにサンプルデータを以下の条件で作成します。
- 期間: 5年間(60か月)
- 季節性: 3月、6月、9月、12月にピークを持つ年4回のパターン(12か月周期)。ピークの振幅(強さ)は、年ごとに変化
- トレンド: 1年毎に上昇トレンドと下降トレンドを繰り返す
- ノイズ: 正規分布に従うランダムノイズ
- 3つの月で外れ値あり
# サンプルデータのパラメータ設定
seed <- 20250508
n_years <- 5
frequency <- 12 # 月次データ
n_months <- n_years * frequency
# 基本となる季節パターン
base_seasonal_pattern <- numeric(12)
base_seasonal_pattern[12] <- 3.0 # December
base_seasonal_pattern[6] <- 2.0 # June
base_seasonal_pattern[3] <- 1.0 # March
base_seasonal_pattern[9] <- -2.5 # September
base_seasonal_pattern[1] <- -0.5
base_seasonal_pattern[2] <- -0.6
base_seasonal_pattern[4] <- -0.3
base_seasonal_pattern[5] <- -0.7
base_seasonal_pattern[7] <- -0.4
base_seasonal_pattern[8] <- -0.5
base_seasonal_pattern[10] <- -0.2
base_seasonal_pattern[11] <- -0.3
# 季節成分の作成 (振幅が年々変化)
seasonal_component_varying <- numeric(n_months)
# 年ごとの振幅スケールファクター (ここでは 0.8から5.2へ線形に増加)
amplitude_scale_factors <- seq(from = 0.8, to = 5.2, length.out = n_years)
for (i in 0:(n_years - 1)) {
year_start_index <- i * frequency + 1
year_end_index <- (i + 1) * frequency
# 現在の年の振幅スケール
current_scale <- amplitude_scale_factors[i + 1]
# スケールを適用した季節パターン
scaled_pattern_for_year <- base_seasonal_pattern * current_scale
# 各年のパターンが合計0になるように中心化
centered_pattern_for_year <- scaled_pattern_for_year - mean(scaled_pattern_for_year)
seasonal_component_varying[year_start_index:year_end_index] <- centered_pattern_for_year
}
# トレンド成分の作成
trend_component_varying_season <- numeric(n_months)
current_trend_value <- 5
for (i in 0:(n_years - 1)) {
year_start_index <- i * frequency + 1
year_end_index <- (i + 1) * frequency
start_val_for_year <- current_trend_value
if (i %% 2 == 0) {
end_val_for_year <- start_val_for_year + 2
trend_component_varying_season[year_start_index:year_end_index] <- seq(from = start_val_for_year, to = end_val_for_year, length.out = frequency)
} else {
end_val_for_year <- start_val_for_year - 2
trend_component_varying_season[year_start_index:year_end_index] <- seq(from = start_val_for_year, to = end_val_for_year, length.out = frequency)
}
current_trend_value <- end_val_for_year
}
# ノイズ成分の作成
set.seed(seed)
noise_component_varying_season <- rnorm(n_months, mean = 0, sd = 0.5)
# 全成分を合成
observed_data_varying_season <- seasonal_component_varying + trend_component_varying_season + noise_component_varying_season
# 外れ値の追加
data_ts_varying_season_outliers_val <- observed_data_varying_season
set.seed(seed)
outlier_indices <- sample(1:n_months, 3)
outlier_magnitudes <- c(10, -12, 15)
data_ts_varying_season_outliers_val[outlier_indices[1]] <- data_ts_varying_season_outliers_val[outlier_indices[1]] + outlier_magnitudes[1]
data_ts_varying_season_outliers_val[outlier_indices[2]] <- data_ts_varying_season_outliers_val[outlier_indices[2]] + outlier_magnitudes[2]
data_ts_varying_season_outliers_val[outlier_indices[3]] <- data_ts_varying_season_outliers_val[outlier_indices[3]] + outlier_magnitudes[3]
# tsオブジェクトに変換
data_ts_varying_season_outliers <- ts(data_ts_varying_season_outliers_val, frequency = frequency, start = c(2020, 1))
true_trend_ts_varying_season <- ts(trend_component_varying_season, frequency = frequency, start = c(2020, 1))
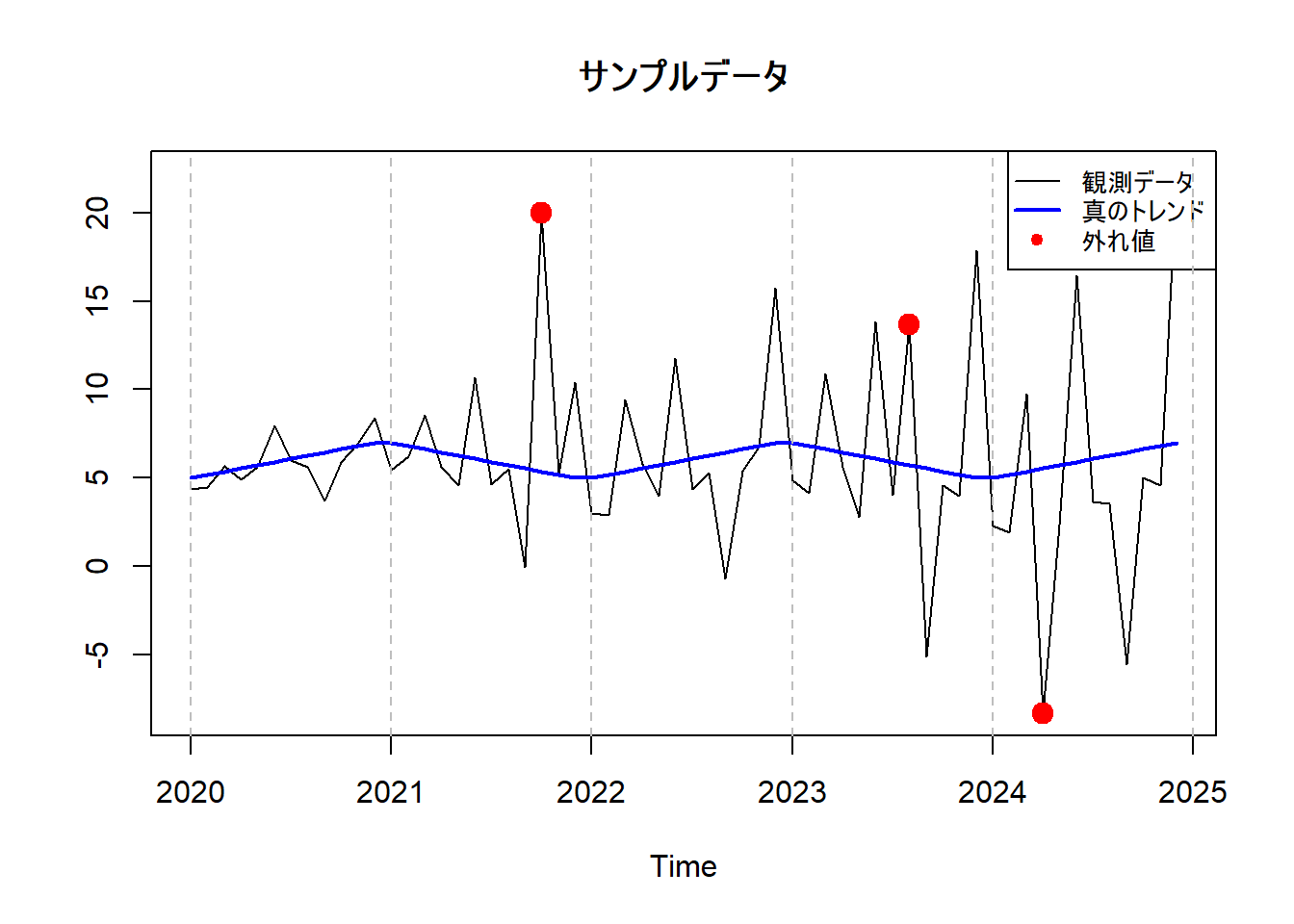
# サンプルデータのプロット
plot(data_ts_varying_season_outliers,
main = "サンプルデータ", ylab = NULL,
ylim = range(c(data_ts_varying_season_outliers, true_trend_ts_varying_season))
)
lines(true_trend_ts_varying_season, col = "blue", lwd = 2)
points(time(data_ts_varying_season_outliers)[outlier_indices],
data_ts_varying_season_outliers[outlier_indices],
col = "red", pch = 19, cex = 1.5
)
legend("topright",
legend = c("観測データ", "真のトレンド", "外れ値"),
col = c("black", "blue", "red"),
lty = c(1, 1, NA), pch = c(NA, NA, 19), lwd = c(1, 2, NA), cex = 0.8
)
abline(v = seq(2020, 2020 + n_years, by = 1), col = "grey", lty = 2)季節性のピークが1年毎に変化(増加)している様子です。
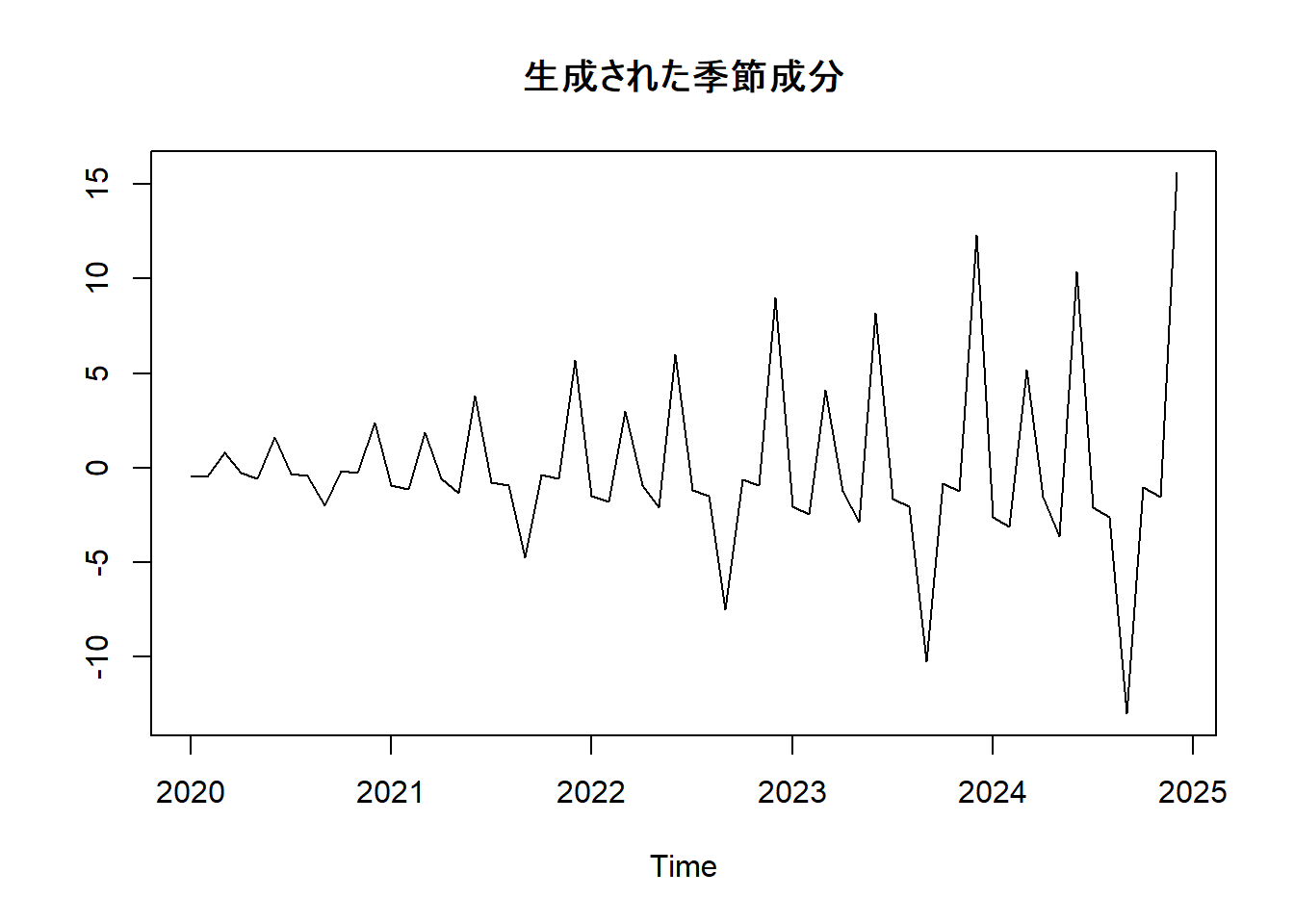
# 生成された季節成分の確認
plot(ts(seasonal_component_varying, frequency = 12, start = c(2020, 1)), main = "生成された季節成分", ylab = NULL)関数 stl の引数を確認します。
args(stl)function (x, s.window, s.degree = 0, t.window = NULL, t.degree = 1,
l.window = nextodd(period), l.degree = t.degree, s.jump = ceiling(s.window/10),
t.jump = ceiling(t.window/10), l.jump = ceiling(l.window/10),
robust = FALSE, inner = if (robust) 1 else 2, outer = if (robust) 15 else 0,
na.action = na.fail)
NULL- x :
- 分解対象となる一次元の時系列データ(tsオブジェクト)。関数 stl はtsオブジェクトの周期情報を使って季節成分を推定しますので周期(frequency)が適切に設定されている必要あり。月次データなら frequency=12、四半期データなら frequency=4 。
- s.window(Seasonal Window) :
- 季節成分の平滑化におけるLoessウィンドウの幅(スパン)。
- 季節性の強さが変化する場合 : スパンを数値で指定。なお、Loess平滑化では中心点を持つため奇数とする必要あり。値が大きいほど、季節パターンは時間を通じてより安定的(変化しにくい)になり、値が小さいほど、季節パターンは時間とともに変化しやすくなります。
- 季節性の強さが変化しない場合 : 文字列 periodic を指定。季節パターンは全期間を通じて固定的であると仮定され、s.window は内部的に非常に大きな値(10 * n + 1)に設定されて、s.degree は0に強制されます。結果として、各サイクル(例 : 各月)の季節効果は全期間で同じ値になります。
- s.degree(Seasonal Degree) :
- 季節成分のLoess平滑化における局所多項式の次数。0か1を指定します。
- 0 : 局所定数モデル(Loess平滑化の各ウィンドウ内で定数でフィット)。
- 1 : 局所線形モデル(Loess平滑化の各ウィンドウ内で線形関数でフィット)。季節性の強さが変化する場合に選択。
- デフォルトは 0 。
- s.window = “periodic” の場合は、自動的に 0 に設定されます。
- t.window(Trend Window) :
- トレンド成分の平滑化におけるLoessウィンドウの幅。トレンド成分の滑らかさを制御します。
- ウィンドウ内のデータ点の数として 奇数の自然数 を指定します。値が大きいほど、トレンドは滑らかになり、値が小さいほどトレンドはデータに追従しやすくなるため、より変動が激しくなる可能性があります。
- デフォルトは NULL。t.window <- nextodd(ceiling(1.5 * frequency / (1 - 1.5 / s.window))) としたスパンが設定されます。よって、s.window が小さい(季節パターンの推定に使われるデータ点数が少ない、季節変動が速い)ほど、t.window は大きくなります(トレンドをより滑らかに、長期的に推定)。
- t.degree(Trend Degree) :
- トレンド成分のLoess平滑化における局所多項式の次数。
- 0 : 局所定数モデル。
- 1 : 局所線形モデル。
- l.window(Low-pass Window) :
- 各サイクル部分系列(例 : 1月のデータのみ、2月のデータのみ)をLoessで平滑化して求めた季節成分の候補から、トレンド成分に近い低周波成分を抽出するためのLoess平滑化ウィンドウ幅。
- ウィンドウ内のデータ点の数として奇数の自然数を指定 。
- 季節変動の周期以上の変動を取り除くことで、トレンドに近い成分を抽出します。
- デフォルトは nextodd(frequency)、つまり時系列の周期と同じ長さ(偶数の場合は+1)に設定されます。
- l.degree(Low-pass Degree) :
- 低域通過フィルタのLoess平滑化における局所多項式の次数。
- 0 : 局所定数モデル。
- 1 : 局所線形モデル。
- デフォルトは t.degree と同じ値です。
- s.jump, t.jump, l.jump(Jump values) :
- Loess平滑化の計算量を削減するためのパラメータ。
- 各ウィンドウ(s.window, t.window,l.window)に対応。Loess平滑化は各データ点に対して行われますが、jump 値を指定すると、jump 個おきに平滑化計算を行い、その間の点は補間によって求めます。
- スキップするデータ点の数を 自然数 で指定。
- デフォルトはそれぞれ対応するウィンドウサイズの約10%(ceiling(window/10)) です。
- robust :
- 外れ値に対してロバストな分解を行うかどうかを指定する論理値。
- TRUE : ロバスト推定を行います。残差に基づいてロバスト重みが計算され、Loess平滑化時に使用されます。これにより、外れ値が季節成分やトレンド成分の推定に与える影響が軽減されます。
- FALSE : ロバスト推定を行いません(デフォルト)。
- inner(Inner loop iterations) :
- 内部ループの反復回数。
- 自然数で指定。
- robust = TRUE の場合のデフォルトは 1 。重み付けLoessを用いた分解が1回行われます。
- robust = FALSE の場合のデフォルトは 2 。
- outer(Outer loop iterations) :
- 外部ループ(ロバスト化ループ)の反復回数。
- 自然数で指定。
- robust = TRUE の場合のデフォルトは 15 です。この回数だけ、ロバスト重みの計算と内部ループによる分解が繰り返されます。
- robust = FALSE の場合のデフォルトは 0 であり、外部ループは実行されません。
- na.action :
- 入力時系列 x に欠損値(NA) が含まれる場合の処理方法を指定する関数。
- デフォルトは na.fail で、欠損値が存在するとエラーを発生させて処理を停止します。
- na.omit : 欠損値を含む観測を除外します。
- na.exclude : na.omit と同様に除外しますが、結果の長さを元に戻す際にNAを挿入します。
- na.pass : 欠損値をそのまま処理しようとします。
作成したサンプルデータ data_ts_varying_season_outliers を関数 stl を利用して分解します。
(stl_varying_season_optimal <- stl(
x = data_ts_varying_season_outliers,
s.window = 21,
# サンプルデータの季節性に変動が見られるため、"periodid" とはせずに約2年分弱を指定
s.degree = 1,
# 季節成分のLoess平滑化: 振幅が変化するため、局所線形(1)を指定
t.window = 13,
# トレンドの変動周期(1年=12ヶ月)を捉えられるように、frequency(12) + 1 を指定
t.degree = 1,
# トレンドのLoessは局所線形
# トレンドが局所的に直線的に変化すると仮定
l.window = 13,
# frequency(12) + 1を指定
l.degree = 1,
# 低域通過フィルタのLoess平滑化は局所線形モデル
# t.degreeと同じ値
robust = TRUE
)) Call:
stl(x = data_ts_varying_season_outliers, s.window = 21, s.degree = 1,
t.window = 13, t.degree = 1, l.window = 13, l.degree = 1,
robust = TRUE)
Components
seasonal trend remainder
Jan 2020 -0.38249490 4.691076 0.03270171
Feb 2020 -0.38437542 4.891896 -0.04737980
Mar 2020 0.77478146 5.092716 -0.19855611
Apr 2020 -0.36815300 5.287060 0.01885019
May 2020 -0.16146399 5.481404 0.27927600
Jun 2020 2.32022872 5.676443 -0.04683974
Jul 2020 -0.24130784 5.871482 0.37223413
Aug 2020 0.03247703 6.013623 -0.41047585
Sep 2020 -2.73559613 6.155765 0.28134556
Oct 2020 -0.47082471 6.254601 0.12554069
Nov 2020 0.65127419 6.353438 -0.06958363
Dec 2020 1.92514151 6.353684 0.13481500
Jan 2021 -1.06417819 6.353931 0.15102866
Feb 2021 -1.19254615 6.293179 1.11326034
Mar 2021 2.13462372 6.232428 0.18611739
Apr 2021 -0.36173686 6.127224 -0.14908482
May 2021 -1.07890861 6.022021 -0.34629421
Jun 2021 4.27089314 5.867796 0.55678368
Jul 2021 -0.82369286 5.713571 -0.24816501
Aug 2021 -0.60363151 5.575324 0.55527839
Sep 2021 -5.07230825 5.437077 -0.39605073
Oct 2021 -0.68167712 5.333905 15.33621957
Nov 2021 0.03186193 5.230732 -0.04027907
Dec 2021 5.40125389 5.254457 -0.25875365
Jan 2022 -1.74598575 5.278181 -0.53772473
Feb 2022 -2.00081406 5.395143 -0.47150010
Mar 2022 3.49439586 5.512105 0.44348783
Apr 2022 -0.35537004 5.678248 0.48371567
May 2022 -1.99638173 5.844391 0.14479166
Jun 2022 6.22154882 6.010690 -0.44215324
Jul 2022 -1.40606687 6.176990 -0.42658832
Aug 2022 -1.23972270 6.324488 0.20366687
Sep 2022 -7.40899668 6.471987 0.25923136
Oct 2022 -0.89250845 6.589479 -0.30049084
Nov 2022 -0.58753184 6.706971 0.63696842
Dec 2022 8.87739145 6.662933 0.21413197
Jan 2023 -2.42776145 6.618895 0.67238218
Feb 2023 -2.80902271 6.487842 0.45474241
Mar 2023 4.85425467 6.356789 -0.29112248
Apr 2023 -0.34887217 6.156610 -0.18629023
May 2023 -2.91367944 5.956431 -0.23613071
Jun 2023 8.17243098 5.824923 -0.14901793
Jul 2023 -1.98816332 5.693416 0.34176652
Aug 2023 -1.87549205 5.626940 9.94190815
Sep 2023 -9.74531902 5.560464 -0.92398564
Oct 2023 -1.10294128 5.506347 0.20690081
Nov 2023 -1.20649471 5.452230 -0.25424223
Dec 2023 12.35397458 5.496392 -0.01151149
Jan 2024 -3.10855895 5.540554 -0.14293130
Feb 2024 -3.61822827 5.665464 -0.14568789
Mar 2024 6.20294578 5.790375 -2.25377687
Apr 2024 -0.34536129 5.904367 -13.88048462
May 2024 -3.82417994 6.018359 0.18270812
Jun 2024 10.12612366 6.120556 0.20289318
Jul 2024 -2.56214081 6.222753 0.00315402
Aug 2024 -2.52312658 6.275283 -0.19240274
Sep 2024 -12.07470589 6.327812 0.22390954
Oct 2024 -1.30987677 6.371602 -0.02081614
Nov 2024 -1.82894836 6.415391 -0.02215355
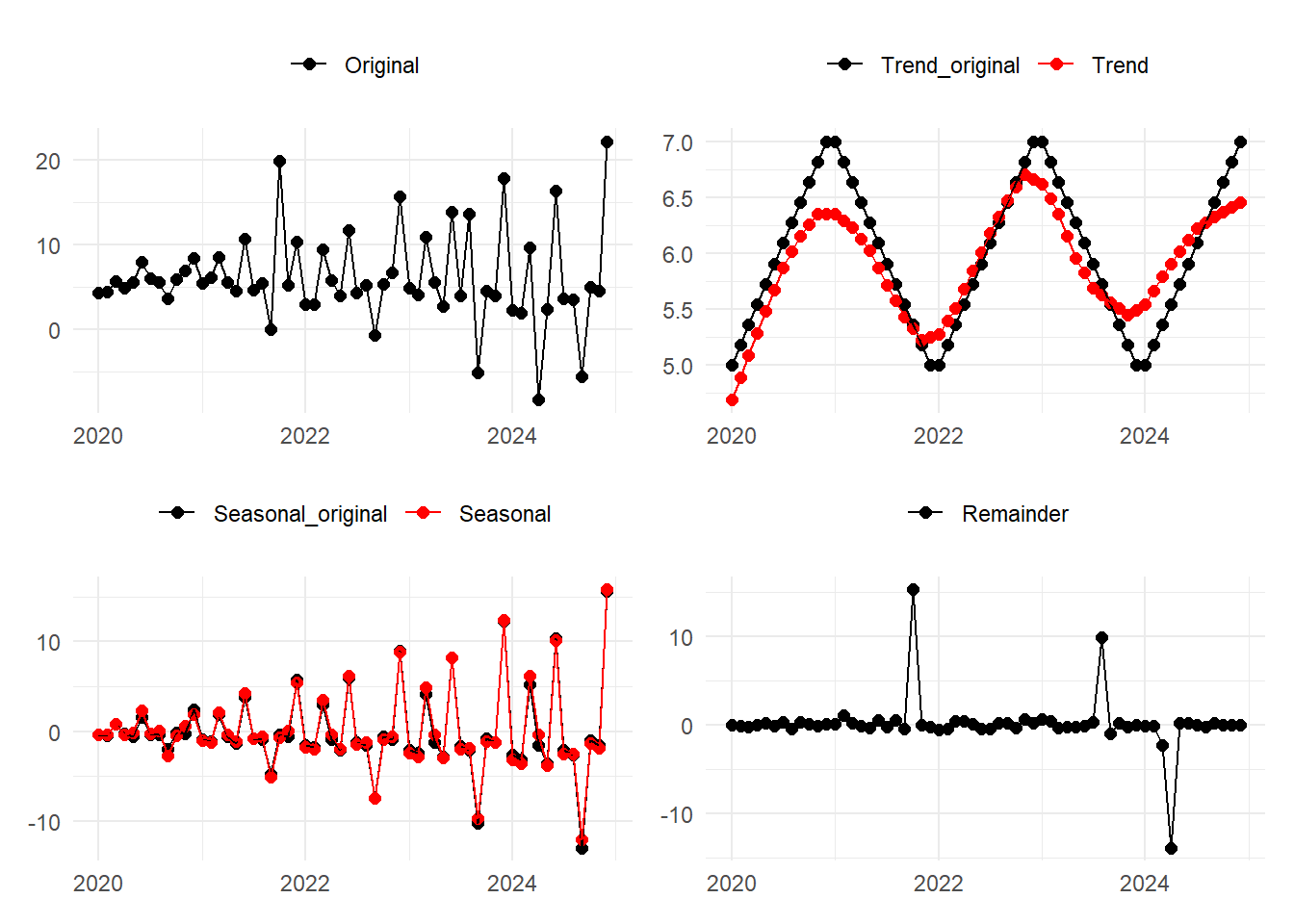
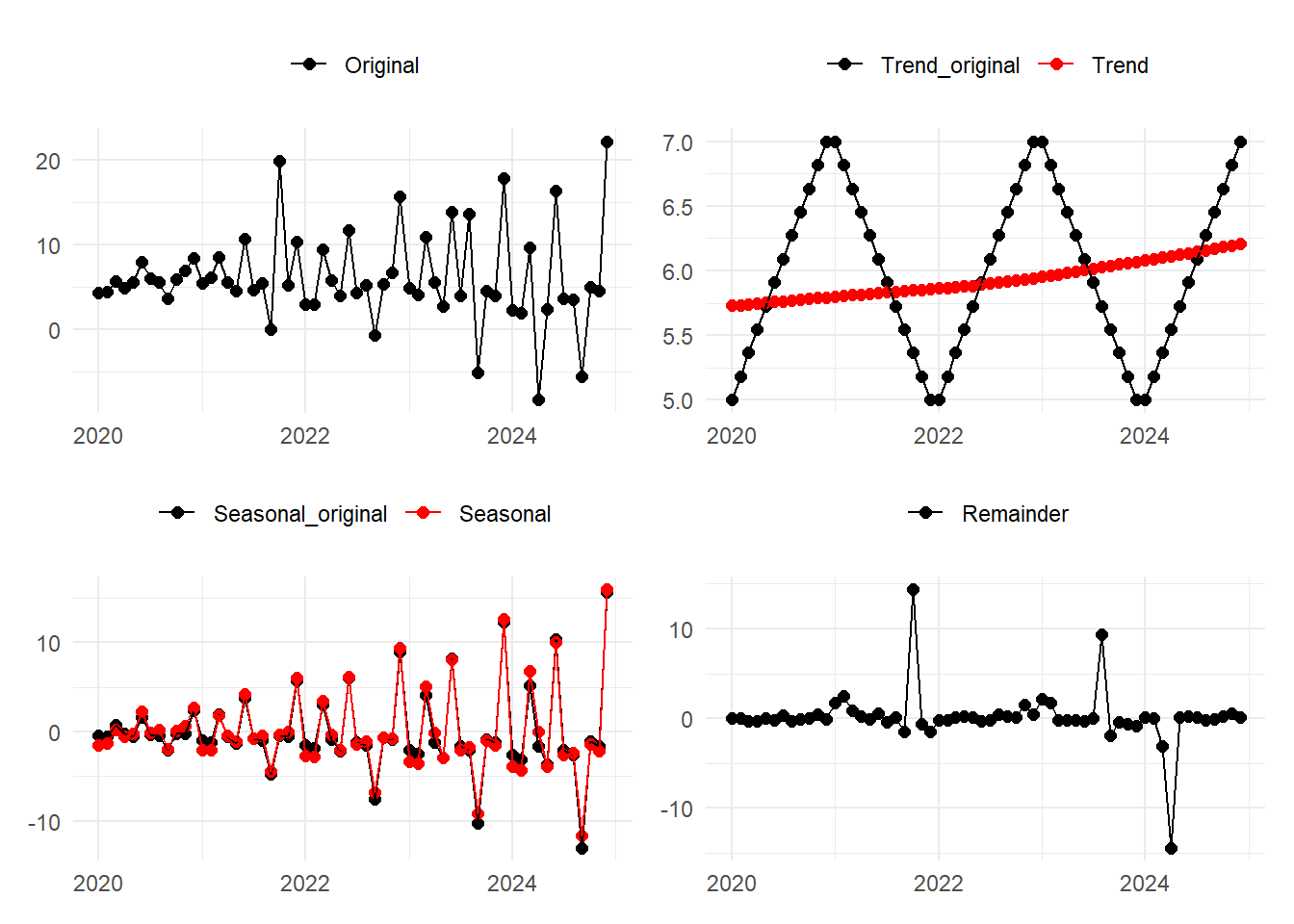
Dec 2024 15.83159905 6.456065 -0.03984246サンプルデータの各成分と比較します。
トレンド成分の山と谷の時点はほぼ一致しており、季節成分のサイクルおよびピークの変化もほぼ追えています。
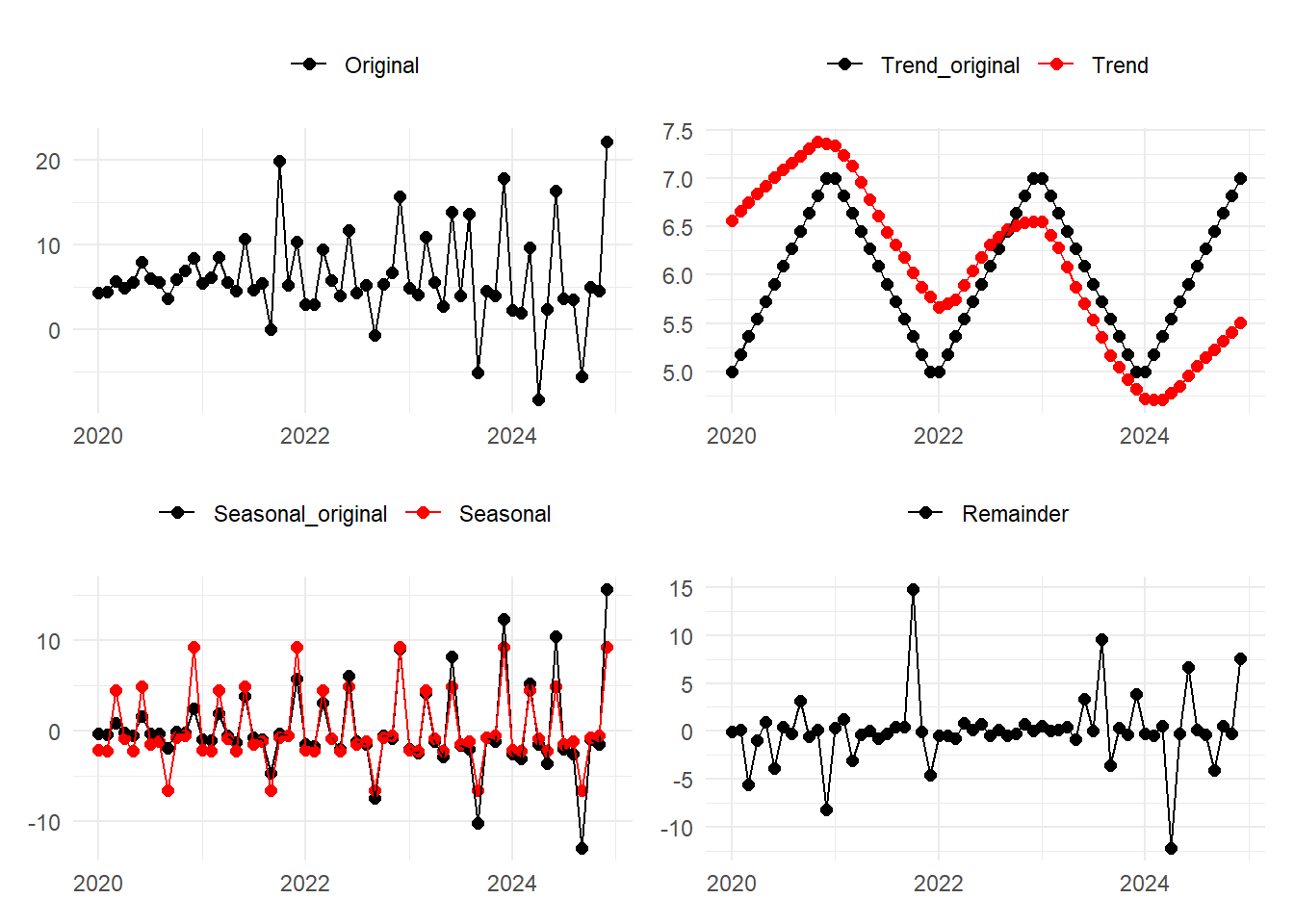
それではサンプルデータの設定と意図的に違えて「季節成分に変化なし」とし、引数 s.window を periodic に指定して分解に掛けます。
stl_varying_season_optimal <- stl(
x = data_ts_varying_season_outliers,
s.window = "periodic",
s.degree = 1, # 但し、s.window = "periodic" であるため 0 として計算される
t.window = 13,
t.degree = 1,
l.window = 13,
l.degree = 1,
robust = TRUE
)季節成分のサイクルは一致していますがピークの変化を追従できていないため、結果としてトレンド、そして残差は Figure 3 より乱れています。
続いて s.window は Figure 3 と同じく 21 としますが、t.window を 12 × 5 + 1 = 61 とします。
stl_varying_season_optimal <- stl(
x = data_ts_varying_season_outliers,
s.window = 21,
s.degree = 1,
t.window = 61,
t.degree = 1,
l.window = 13,
l.degree = 1,
robust = TRUE
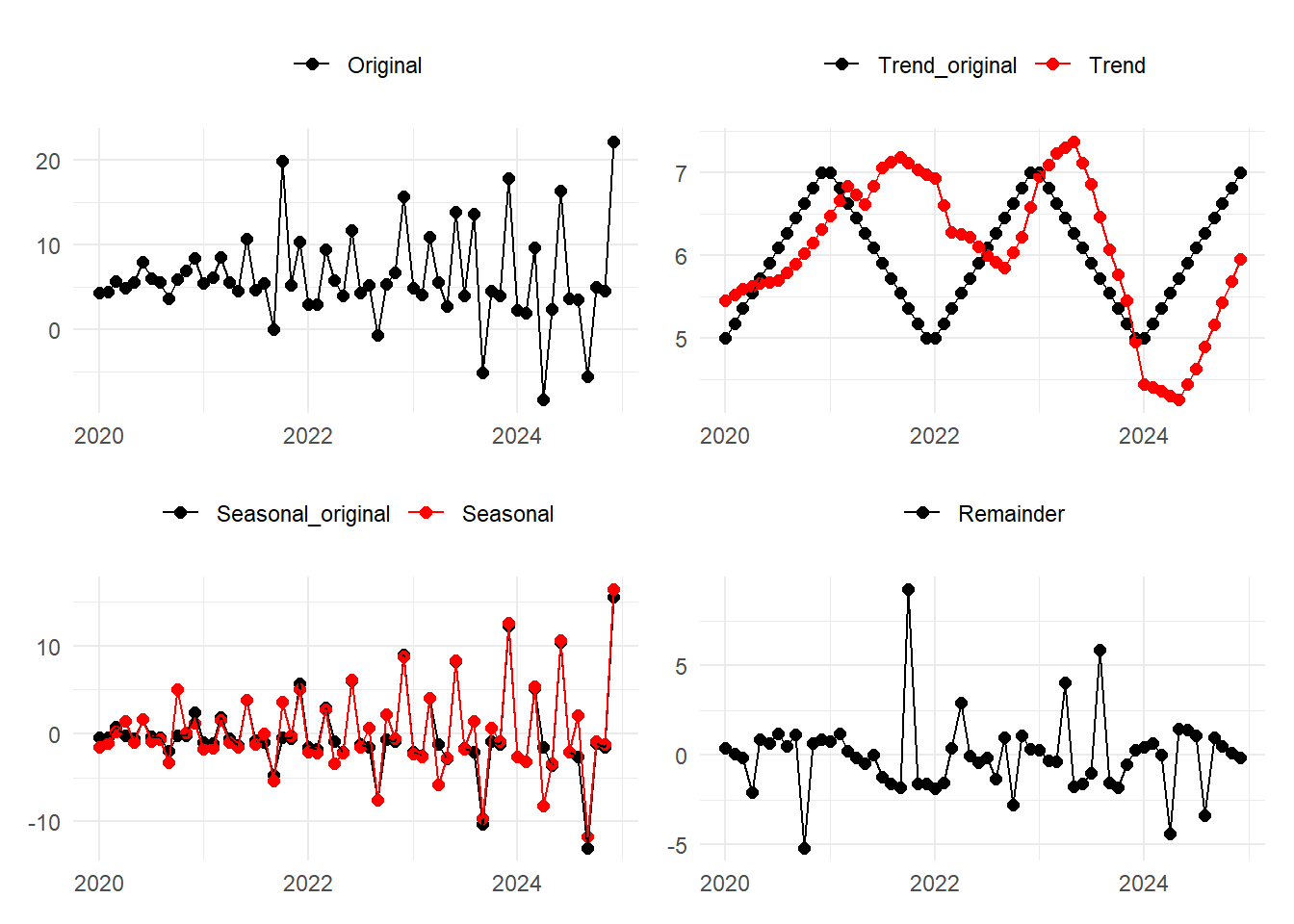
)季節成分のサイクルとピークの変化は追えていますが、トレンドには全く追従できていないため Figure 3 と比較しますと Remainder(残差) の分散が大きくなっていることを確認できます。
最後に robust = FALSE とした場合を確認します。
stl_varying_season_optimal <- stl(
x = data_ts_varying_season_outliers,
s.window = 21,
s.degree = 1,
t.window = 13,
t.degree = 1,
l.window = 13,
l.degree = 1,
robust = FALSE
)季節成分のサイクルとピークの変化は追えていますが、外れ値がトレンドに影響し、結果として残差がかなり 乱れ ます。
以上です。