Rで 線形代数:レーベンバーグ・マーカート法 を試みます。
1. レーベンバーグ・マーカート法(Levenberg-Marquardt Algorithm, LMA)とは
目的
レーベンバーグ・マーカート法(以下、LM法)は、非線形最小二乗問題を解くための、反復最適化アルゴリズムです。
「非線形最小二乗問題」とは、与えられたデータ点群に、パラメータを含む非線形なモデル関数を最もよく当てはめる(フィッティングする)問題です。
具体的には、「実測値」と「モデルの予測値」の差(残差)の二乗和を最小にするような、モデルのパラメータを見つけ出すことを目的とします。
Minimize: S(β) = Σ [yᵢ - f(xᵢ, β)]²
-
yᵢ: i番目の実測値 -
f(xᵢ, β): i番目の入力xᵢとパラメータβを持つ非線形モデルの予測値 -
S(β): 残差平方和。これを最小化したい。
2つの手法の組み合わせ
LM法は、非線形最適化の2つの手法、「ガウス・ニュートン法」と「最急降下法」を組み合わせた、ハイブリッドな手法です。
- ガウス・ニュートン法 (Gauss-Newton method)
- 長所: 解の近くでは、二次収束に近いため非常に収束が速い。
- 短所: 解から遠い場所では不安定になりやすく、発散してしまうことがある。
- 最急降下法 (Gradient Descent method)
- 長所: どんな場所からスタートしても、とりあえず目的関数の値が減少する方向に進むため、安定している(頑健性が高い)。
- 短所: 解の近くで収束が非常に遅くなる。
LM法は、この2つの手法を「ダンピングパラメータ λ (ラムダ)」を使って自動的に切り替えます。
LM法のアルゴリズム
LM法は、各ステップでパラメータの更新量 h を以下の修正された方程式を解くことで求めます。
(JᵀJ + λI) h = Jᵀr
-
J: ヤコビ行列(モデル関数を各パラメータで偏微分した行列)。関数の局所的な傾きを表します。 -
r: 残差ベクトル(実測値 – 予測値)。 -
h: パラメータの更新量ベクトル。 -
λ: ダンピングパラメータ。 -
I: 単位行列。
このダンピングパラメータ λ の値によって、アルゴリズムの挙動が変わります。
-
λが小さい (ほぼ 0) の場合:-
(JᵀJ) h = Jᵀrとなり、これはガウス・ニュートン法そのものです。 - モデルの当てはまりが良い(解に近い)と判断された場合、
λを小さくして収束を加速させます。
-
-
λが大きい場合:-
JᵀJに比べてλIが支配的になり、方程式はλh ≈ Jᵀrのようになります。これは最急降下法と似た動きになります(hが勾配Jᵀrとほぼ同じ方向を向く)。 - モデルの当てはまりが悪い(解から遠い)と判断された場合、
λを大きくして、安定した最急降下法に近い動きで探索を進めます。
-
このように、LM法は「上手くいっているときはガウス・ニュートン法で一気に進み、上手くいかないときは最急降下法で安全に進む」という戦略を、λの値を調整することで自動的に実行するアルゴリズムです。
2. Rによるシミュレーション
シナリオ: 指数減衰曲線 y = A * exp(-k * x) にノイズが乗ったデータを生成し、このデータから元のパラメータ A と k をLM法で推定します。
Rコード
# --------------------------------------------------
# レーベンバーグ・マーカート法のシミュレーション
# --------------------------------------------------
library(minpack.lm)
# --- 1. データの生成 ---
# 真のパラメータを設定
A_true <- 100
k_true <- 0.5
# モデル関数を定義
model_func <- function(x, A, k) {
A * exp(-k * x)
}
# xデータを生成
x_data <- seq(0, 5, length.out = 50)
# 真のモデルからyデータを生成し、ノイズを加える
seed <- 20250625
set.seed(seed)
y_noise <- rnorm(length(x_data), mean = 0, sd = 5)
y_data <- model_func(x_data, A_true, k_true) + y_noise
# 生成したデータをプロットして確認
# plot(x_data, y_data, main = "Generated Data with Noise", xlab = "Time (x)", ylab = "Value (y)", pch = 16)
# curve(model_func(x, A_true, k_true), from=0, to=5, col="red", lwd=2, add=TRUE)
# legend("topright", legend=c("Noisy Data", "True Model"), col=c("black", "red"), pch=c(16, NA), lty=c(NA, 1))
# --- 2. LM法による非線形最小二乗フィッティング ---
# (a) 残差関数を定義
# nls.lm()は、パラメータベクトル par を受け取り、
# 残差ベクトル(実測値 - 予測値)を返す関数を要求する
residual_func <- function(par, x, y_obs) {
A <- par[1]
k <- par[2]
y_pred <- model_func(x, A, k)
# 残差を返す
residuals <- y_obs - y_pred
return(residuals)
}
# (b) パラメータの初期値を設定
# 意図的に離れた初期値から開始
par_start <- c(A = 80, k = 0.3)
cat("初期パラメータ GUESS: A =", par_start[1], ", k =", par_start[2], "\n")
# (c) nls.lm() を実行してLM法で最適化
# controlオプションで詳細なトレース情報を表示できる
fit_lm <- nls.lm(
par = par_start,
fn = residual_func,
x = x_data,
y_obs = y_data,
control = nls.lm.control(nprint = 1)
) # nprint=1で各ステップの情報を表示
# --- 3. 結果の確認 ---
# (a) 最適化結果のサマリーを表示
cat("\n--- Optimization Summary ---\n")
summary(fit_lm)
# (b) 推定されたパラメータを取得
par_estimated <- coef(fit_lm)
cat("\n推定されたパラメータ (A, k):\n")
print(par_estimated)
cat("\n真のパラメータ (A, k):\n")
print(c(A_true, k_true))
# (c) 結果をプロットして比較
plot(x_data, y_data,
main = "Levenberg-Marquardt Fitting Result",
pch = 16, col = "grey"
)
# 推定されたパラメータで曲線を描画
curve(model_func(x, par_estimated[1], par_estimated[2]),
from = 0, to = 5, col = "blue", lwd = 2, add = TRUE
)
# 真のモデルも点線で描画
curve(model_func(x, A_true, k_true),
from = 0, to = 5, col = "red", lty = 2, lwd = 2, add = TRUE
)
legend("topright",
legend = c("Noisy Data", "Fitted Model (LM)", "True Model"),
col = c("grey", "blue", "red"),
pch = c(16, NA, NA),
lty = c(NA, 1, 2),
lwd = 2
)初期パラメータ GUESS: A = 80 , k = 0.3
It. 0, RSS = 5246.14, Par. = 80 0.3
It. 1, RSS = 1265.3, Par. = 94.7589 0.459593
It. 2, RSS = 1161.69, Par. = 98.0321 0.492137
It. 3, RSS = 1161.27, Par. = 98.2437 0.494313
It. 4, RSS = 1161.27, Par. = 98.2531 0.494415
It. 5, RSS = 1161.27, Par. = 98.2535 0.49442
--- Optimization Summary ---
Parameters:
Estimate Std. Error t value Pr(>|t|)
A 98.25353 2.16785 45.32 <2e-16 ***
k 0.49442 0.01686 29.33 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.919 on 48 degrees of freedom
Number of iterations to termination: 5
Reason for termination: Relative error in the sum of squares is at most `ftol'.
推定されたパラメータ (A, k):
A k
98.2535289 0.4944199
真のパラメータ (A, k):
[1] 100.0 0.5実行結果と解説
- 各ステップの情報を見ると、反復(
It.)ごとに残差平方和(RSS)が減少していく様子がわかります。これがLM法が最適解を探している過程です。 - 推定されたパラメータ (
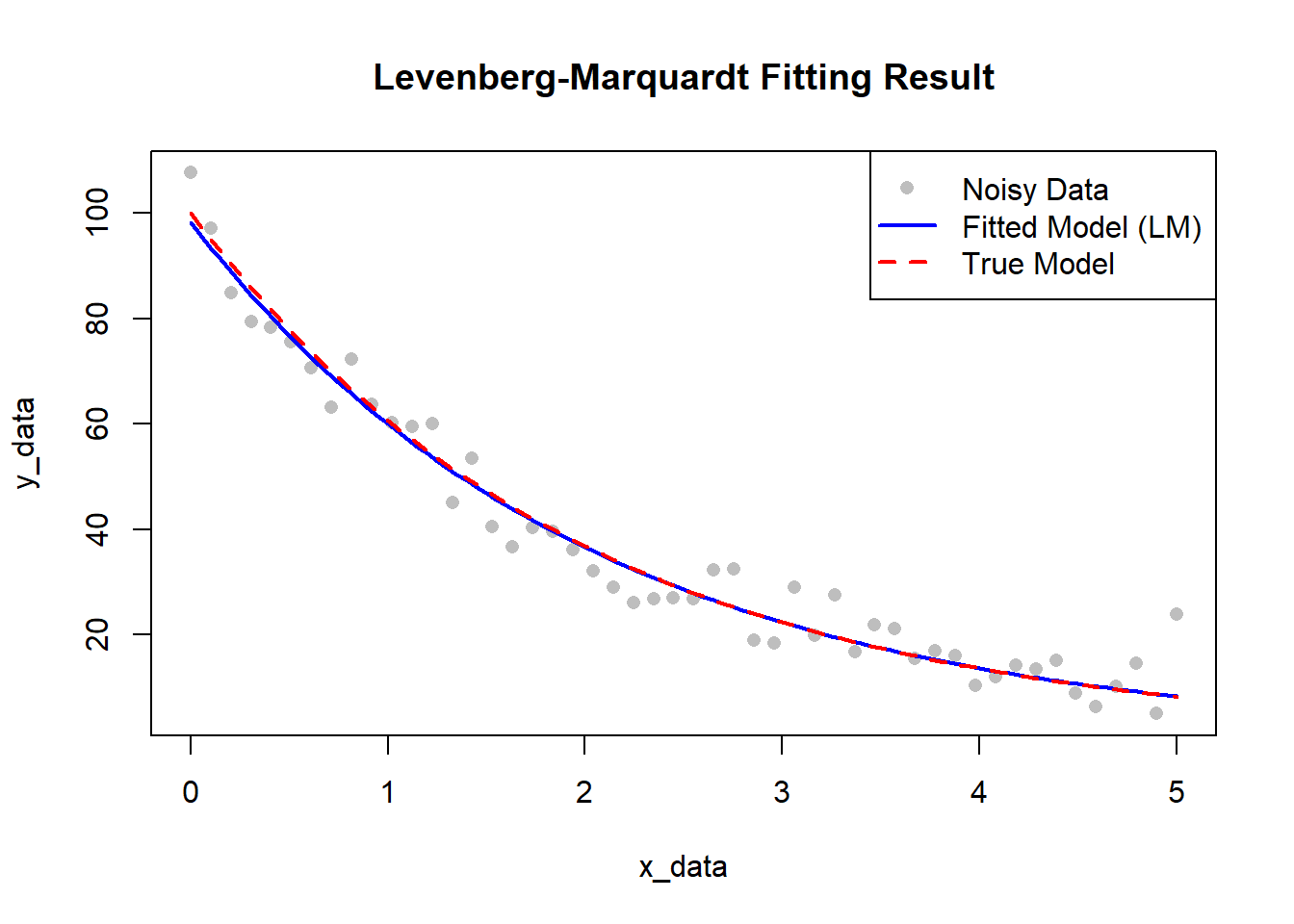
A≈98.3,k≈0.49) は、真のパラメータ (A=100,k=0.5) に近い値となっています。 - プロット図: Figure 1
- 灰色の点: ノイズを含んだ観測データ。
- 赤い点線: 「真の」モデル。
- 青い実線: LM法により推定したパラメータから描かれた「最適な」モデル。
以上です。