Rで 線形代数:直交行列 を確認します。
1. 直交行列(Orthogonal Matrix)とは
定義
ある正方行列 Q が直交行列であるとは、その転置行列 Qᵀ が逆行列 Q⁻¹ と等しくなる行列のことを指します。
数式で書くと以下のようになります。
Qᵀ = Q⁻¹
この定義から、以下の関係式が導かれます。
QᵀQ = QQᵀ = I (I は単位行列)
つまり、直交行列とは「転置しただけで逆行列の働きをする行列」と言えます。
列(または行)ベクトルの性質
QᵀQ = I という式は、直交行列の列ベクトルが持つ幾何学的な性質を表しています。
行列 Q の列ベクトルを q₁, q₂, ..., qₙ とすると、QᵀQ の計算結果は、これらの列ベクトルのすべての組み合わせの内積になります。
この結果が単位行列 I になるということは、以下の2つの条件を満たすことを意味します。
正規性 (Normality): 各列ベクトルの長さ(ノルム)は 1 である。
qᵢ ⋅ qᵢ = ||qᵢ||² = 1直交性 (Orthogonality): 異なる列ベクトル同士は互いに直交している(内積が 0)。
qᵢ ⋅ qⱼ = 0(ただしi ≠ j)
このように、列ベクトル(または行ベクトル)が互いに直交し、かつそれぞれの長さが1であるようなベクトルの組を正規直交基底 (Orthonormal Basis) と呼びます。
つまり、直交行列とは、その列ベクトル(または行ベクトル)が正規直交基底をなす行列である、と言い換えることができます。
幾何学的な意味:形を変えない「剛体変換」
直交行列が表す線形変換は、「図形の形(長さや角度)を一切変えない変換」です。これを剛体変換 (Rigid Transformation) や等長変換 (Isometry) と呼びます。
具体的には、以下の2種類の操作のみを表します。
- 回転 (Rotation): 図形を原点を中心に回転させる。
- 鏡映 (Reflection): 図形を特定の軸(または平面)に対して反転させる(鏡に映す)。
直交行列は、拡大・縮小や、せん断(歪ませる)のような形を変える操作を含みません。なぜなら、ベクトルの長さを変えない変換だからです。
その他の性質
- 行列式: 直交行列の行列式は必ず 1 または -1 になります。
-
det(Q) = 1: 回転を表します(向きを維持)。 -
det(Q) = -1: 鏡映(または回転+鏡映)を表します(向きを反転)。
-
- 計算の利点: 逆行列の計算は一般的にコストが高いですが、直交行列であれば転置するだけで済むため、数値計算において効率的です。この性質から、QR分解や特異値分解など、多くの行列分解アルゴリズムで利用されます。
2. Rによるシミュレーション
ここでは、QR分解を用いて任意の行列から直交行列を生成し、その性質を検証します。
QR分解とは?
任意の行列 A を、直交行列 Q と上三角行列 R の積に分解する手法です (A = QR)。このとき得られる Q が直交行列です。
Rコード
# --------------------------------------------------
# 直交行列のシミュレーション
# --------------------------------------------------
# --- シナリオ1: 直交行列の作成と性質の確認 ---
cat("--- シナリオ1: 直交行列の作成と性質の確認 ---\n")
# 1. 元となる適当な行列を作成
seed <- 20250624
set.seed(seed)
A <- matrix(rnorm(9), nrow = 3)
# 2. QR分解を用いて直交行列Qを抽出
# qr()関数でQR分解を行い、qr.Q()でQを取り出す
Q <- qr.Q(qr(A))
cat("生成された直交行列 Q:\n")
print(Q)
# 3. 性質の確認
# (a) Q^T * Q = I となるか?
cat("\n(a) Q^T * Q の計算結果:\n")
QtQ <- t(Q) %*% Q
print(round(QtQ, 10)) # 計算誤差を考慮して丸める
cat("→ 単位行列になりました。\n")
# (b) Qの転置行列が、Qの逆行列と一致するか?
cat("\n(b) 転置行列と逆行列の比較:\n")
Q_transpose <- t(Q)
Q_inverse <- solve(Q)
cat("Qの転置行列:\n")
print(round(Q_transpose, 5))
cat("Qの逆行列:\n")
print(round(Q_inverse, 5))
cat("→ 両者が一致していることがわかります。\n")
# (c) 行列式が 1 または -1 になるか?
cat("\n(c) 行列式の計算結果:\n")
det_Q <- det(Q)
cat("det(Q) =", det_Q, "\n")
cat("→ 行列式が 1 になりました (これは鏡映を含む変換を意味します)。\n\n")
# --- シナリオ2: 幾何学的な意味の可視化 ---
cat("--- シナリオ2: 幾何学的な意味の可視化 ---\n")
# 2次元の例で可視化する
# (a) 回転を表す直交行列 (det=1)
theta <- pi / 6 # 30度
R_matrix <- matrix(c(cos(theta), sin(theta), -sin(theta), cos(theta)), nrow = 2)
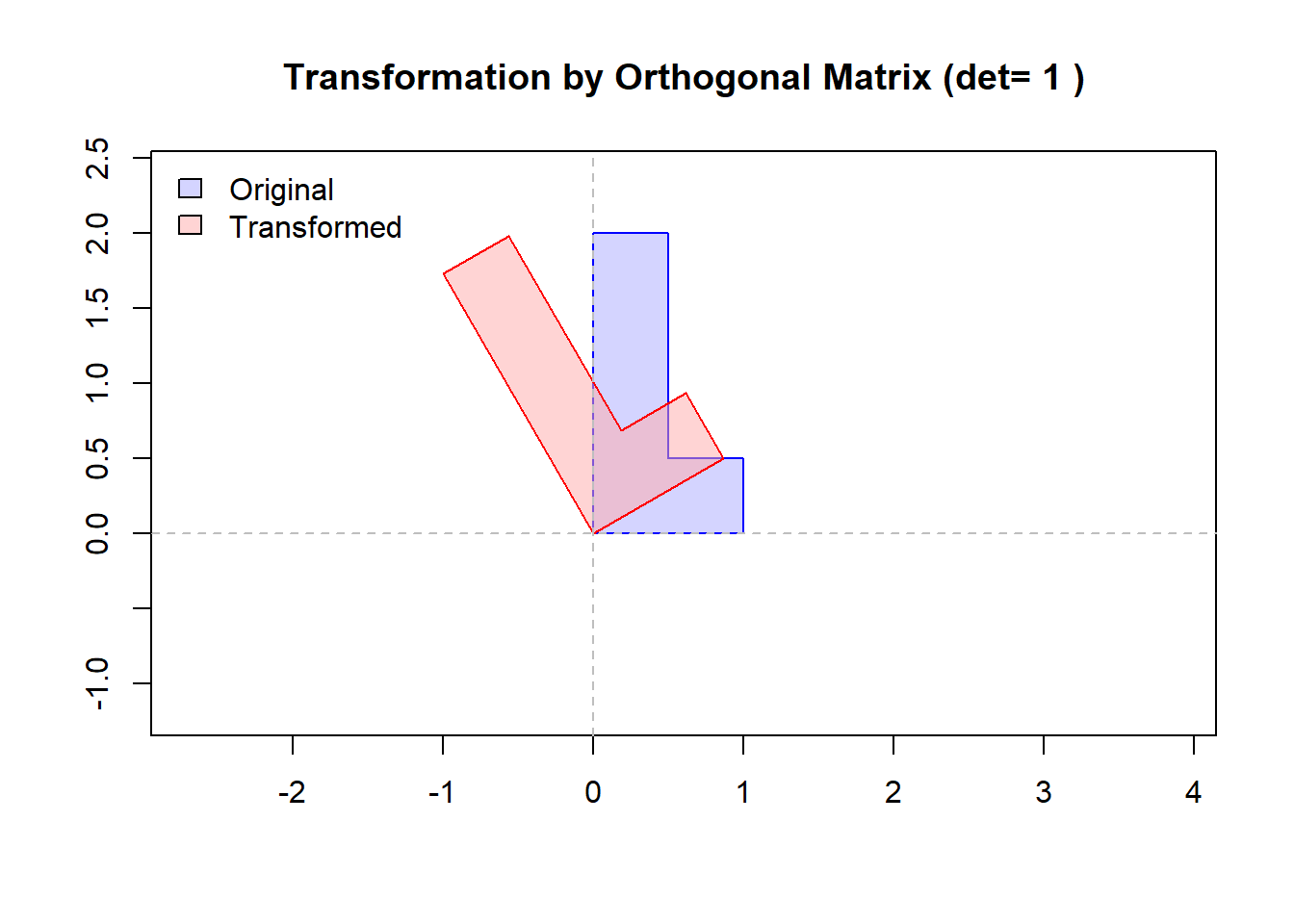
cat("回転行列 R (det=", round(det(R_matrix), 2), ") Figure 1:\n")
print(R_matrix)
# (b) 鏡映を表す直交行列 (det=-1)
# y軸に対する鏡映
F_matrix <- matrix(c(-1, 0, 0, 1), nrow = 2)
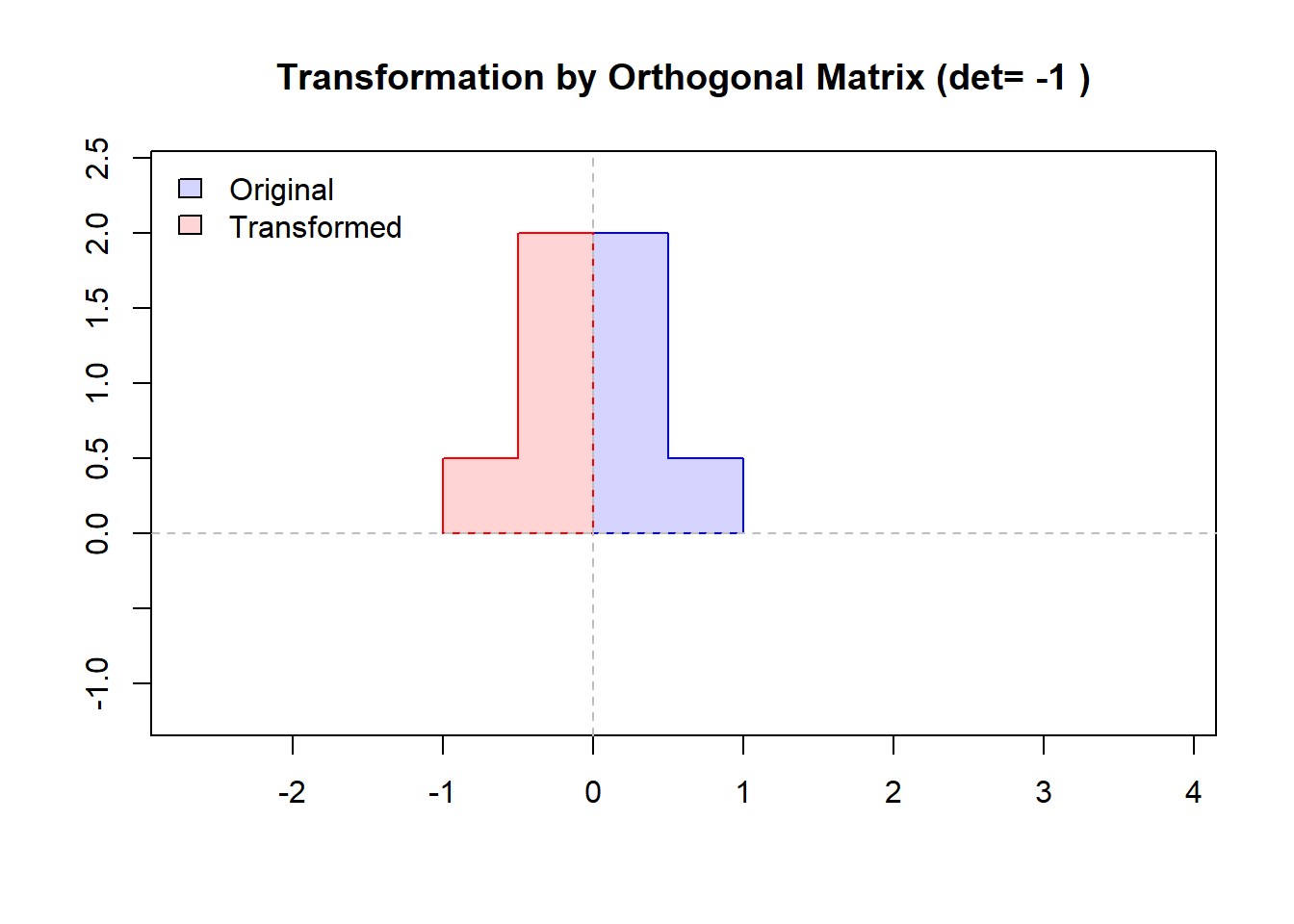
cat("\n鏡映行列 F (det=", round(det(F_matrix), 2), ") Figure 2:\n")
print(F_matrix)
# 描画用の関数
plot_rigid_transform <- function(M, shape) {
transformed_shape <- t(M %*% t(shape))
all_points <- rbind(shape, transformed_shape)
plot_range <- range(all_points) * 1.2
plot(NULL,
xlim = plot_range, ylim = plot_range, asp = 1,
main = paste("Transformation by Orthogonal Matrix (det=", round(det(M), 2), ")"), xlab = "", ylab = ""
)
polygon(shape, col = "#AAAAFF80", border = "blue")
polygon(transformed_shape, col = "#FFAAAA80", border = "red")
abline(h = 0, v = 0, lty = 2, col = "grey")
legend("topleft",
legend = c("Original", "Transformed"),
fill = c("#AAAAFF80", "#FFAAAA80"), bty = "n"
)
}
# 変換対象の図形 (非対称なL字型)
l_shape <- rbind(c(0, 0), c(1, 0), c(1, 0.5), c(0.5, 0.5), c(0.5, 2), c(0, 2), c(0, 0))
# 回転のプロット
plot_rigid_transform(R_matrix, l_shape)
# 鏡映のプロット
plot_rigid_transform(F_matrix, l_shape)--- シナリオ1: 直交行列の作成と性質の確認 ---
生成された直交行列 Q:
[,1] [,2] [,3]
[1,] -0.1273933 0.2846861 -0.9501183
[2,] 0.9047065 -0.3592835 -0.2289573
[3,] -0.4065428 -0.8887459 -0.2117870
(a) Q^T * Q の計算結果:
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
→ 単位行列になりました。
(b) 転置行列と逆行列の比較:
Qの転置行列:
[,1] [,2] [,3]
[1,] -0.12739 0.90471 -0.40654
[2,] 0.28469 -0.35928 -0.88875
[3,] -0.95012 -0.22896 -0.21179
Qの逆行列:
[,1] [,2] [,3]
[1,] -0.12739 0.90471 -0.40654
[2,] 0.28469 -0.35928 -0.88875
[3,] -0.95012 -0.22896 -0.21179
→ 両者が一致していることがわかります。
(c) 行列式の計算結果:
det(Q) = 1
→ 行列式が 1 になりました (これは鏡映を含む変換を意味します)。
--- シナリオ2: 幾何学的な意味の可視化 ---
回転行列 R (det= 1 ) Figure 1:
[,1] [,2]
[1,] 0.8660254 -0.5000000
[2,] 0.5000000 0.8660254
鏡映行列 F (det= -1 ) Figure 2:
[,1] [,2]
[1,] -1 0
[2,] 0 1実行結果と解説
シナリオ1では、QR分解で生成した行列Qが、直交行列の定義QᵀQ = Iや性質Qᵀ = Q⁻¹、det(Q) = ±1をすべて満たしていることが数値的に確認できます。
シナリオ2では、直交行列が表す幾何学的な変換を可視化します。
回転のプロット(Figure 1) 青いL字型の図形が、原点を中心に30度回転して赤い図形になっています。図形の大きさ、辺の長さ、角の角度は一切変わっていません。これは
det(R_matrix) = 1のケースです。鏡映のプロット(Figure 2) 青いL字型の図形が、y軸を基準に鏡で映したように反転し、赤い図形になっています。こちらも図形の大きさや形は変わりませんが、向きが反転しています。これが
det(F_matrix) = -1のケースです。
以上です。