Rで線形代数:行列式

# --------------------------------------------------
# 行列式のシミュレーション
# --------------------------------------------------

# --- シナリオ1: 基本的な計算と逆行列との関係 ---

cat("--- シナリオ1: 基本的な計算と逆行列との関係 ---\n")

# (a) 正則行列の場合
A <- matrix(c(3, 1, 2, 2), nrow = 2)
cat("正則行列 A:\n")
print(A)

det_A <- det(A)
cat("Aの行列式 det(A):", det_A, "\n")
cat("手計算: 3*2 - 1*2 =", 3 * 2 - 2 * 1, "\n")
cat("→ 行列式が0ではないので、逆行列は存在する。\n")
# 実際に逆行列を計算してみる
print(solve(A))

# (b) 特異行列の場合
B <- matrix(c(1, 2, 2, 4), nrow = 2)
cat("\n特異行列 B:\n")
print(B)

det_B <- det(B)
cat("Bの行列式 det(B):", det_B, "\n")
cat("→ 行列式が0なので、逆行列は存在しません。\n")
# solve(B) を実行するとエラーになる
result <- tryCatch(
  {
    solve(B)
  },
  error = function(e) {
    return(e) # エラーオブジェクトを返す
  }
)
print(result$message)

cat("\n\n")


# --- シナリオ2: 幾何学的な意味の可視化 ---

cat("--- シナリオ2: 幾何学的な意味の可視化 ---\n")

# 描画用の関数を定義
plot_transform <- function(M) {
  # 元の単位正方形の頂点（ポリゴン描画用に始点を末尾に追加）
  square_orig_poly <- rbind(c(0, 0), c(1, 0), c(1, 1), c(0, 1), c(0, 0))

  # 行列Mで頂点を変換
  square_transformed_poly <- t(M %*% t(square_orig_poly))

  # 元の基底ベクトル e1=(1,0), e2=(0,1)
  e1 <- c(1, 0)
  e2 <- c(0, 1)

  # 変換後の基底ベクトル v1, v2
  v1 <- M %*% e1
  v2 <- M %*% e2

  # 描画範囲を、元の図形と変換後の図形の両方が収まるように自動調整
  all_points <- rbind(square_orig_poly, square_transformed_poly)
  max_val <- max(abs(all_points)) * 1.2
  plot(NULL,
    xlim = c(-max_val, max_val), ylim = c(-max_val, max_val),
    xlab = "x", ylab = "y", asp = 1,
    main = paste("Determinant (det) =", round(det(M), 2))
  )

  # 軸線を追加
  abline(h = 0, v = 0, lty = 2, col = "grey")

  # 1. 元の単位正方形を描画 (半透明の薄い青)
  polygon(square_orig_poly, col = "#AAAAFF80", border = "blue")

  # 2. 変換後の平行四辺形を描画 (半透明の薄い赤)
  polygon(square_transformed_poly, col = "#FFAAAA80", border = "red")

  # 3. 元の基底ベクトルを点線の矢印で描画
  arrows(0, 0, e1[1], e1[2], col = "blue", lty = 2, lwd = 2.5, length = 0.1)
  arrows(0, 0, e2[1], e2[2], col = "red", lty = 2, lwd = 2.5, length = 0.1)

  # 4. 変換後の基底ベクトルを実線の矢印で描画
  arrows(0, 0, v1[1], v1[2], col = "blue", lwd = 2.5, length = 0.1)
  arrows(0, 0, v2[1], v2[2], col = "red", lwd = 2.5, length = 0.1)

  # 5. 凡例を追加（元の図形と変換後の図形を区別）
  legend("topleft",
    legend = c("Original (Area & Vectors)", "Transformed (Area & Vectors)"),
    col = c("blue", "red"),
    border = c("blue", "red"),
    fill = c("#AAAAFF80", "#FFAAAA80"),
    lty = c(2, 1),
    lwd = 2,
    bty = "n",
    merge = TRUE
  ) # merge=TRUE で塗りつぶしと線を結合
}



# (a) 拡大・回転 (det > 0)
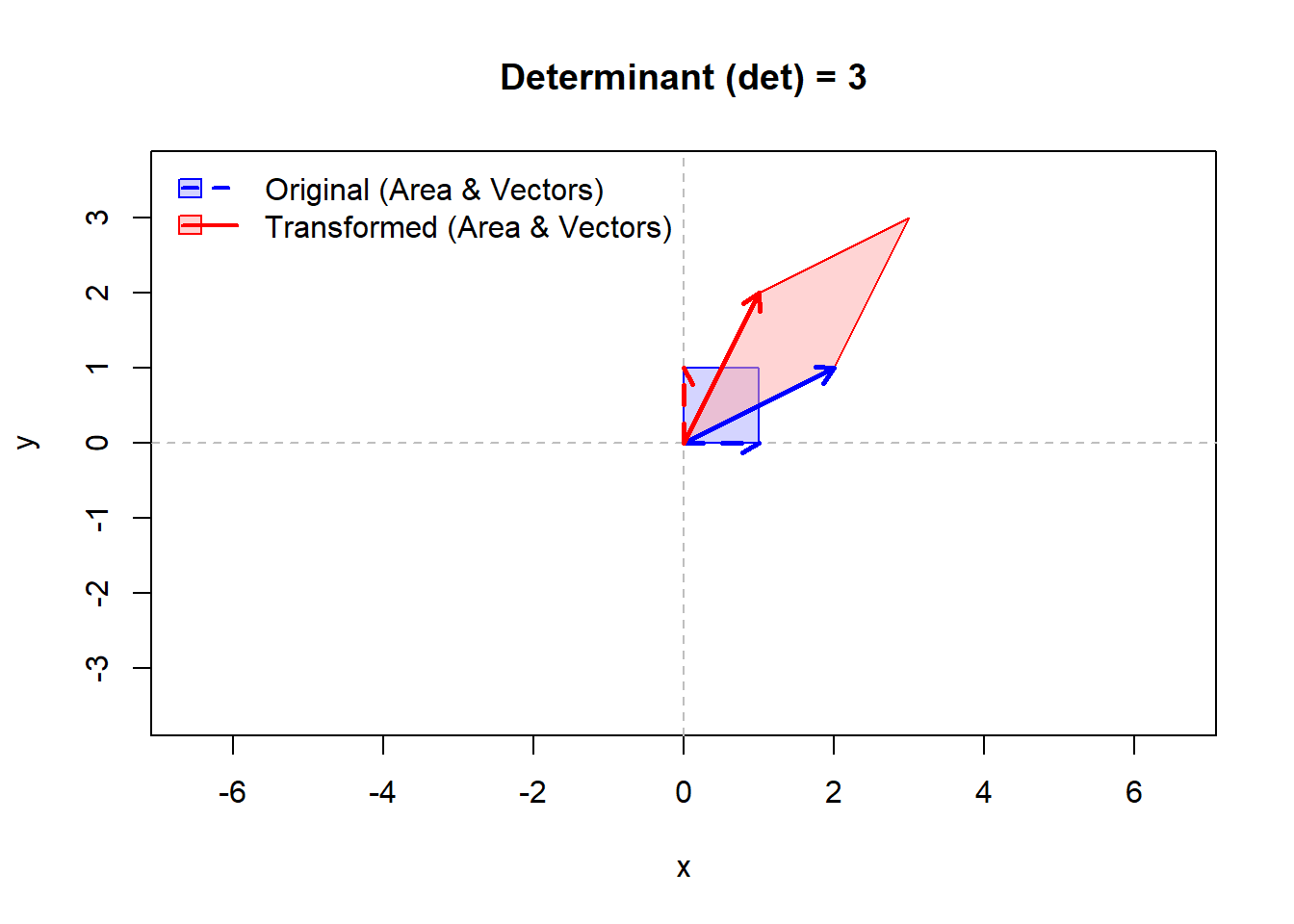
M1 <- matrix(c(2, 1, 1, 2), nrow = 2)
cat("行列 M1:\n")
print(M1)
cat("det(M1) =", det(M1), "(面積が3倍になります。Figure 1)\n")
plot_transform(M1)


# (b) 向きが反転 (det < 0)
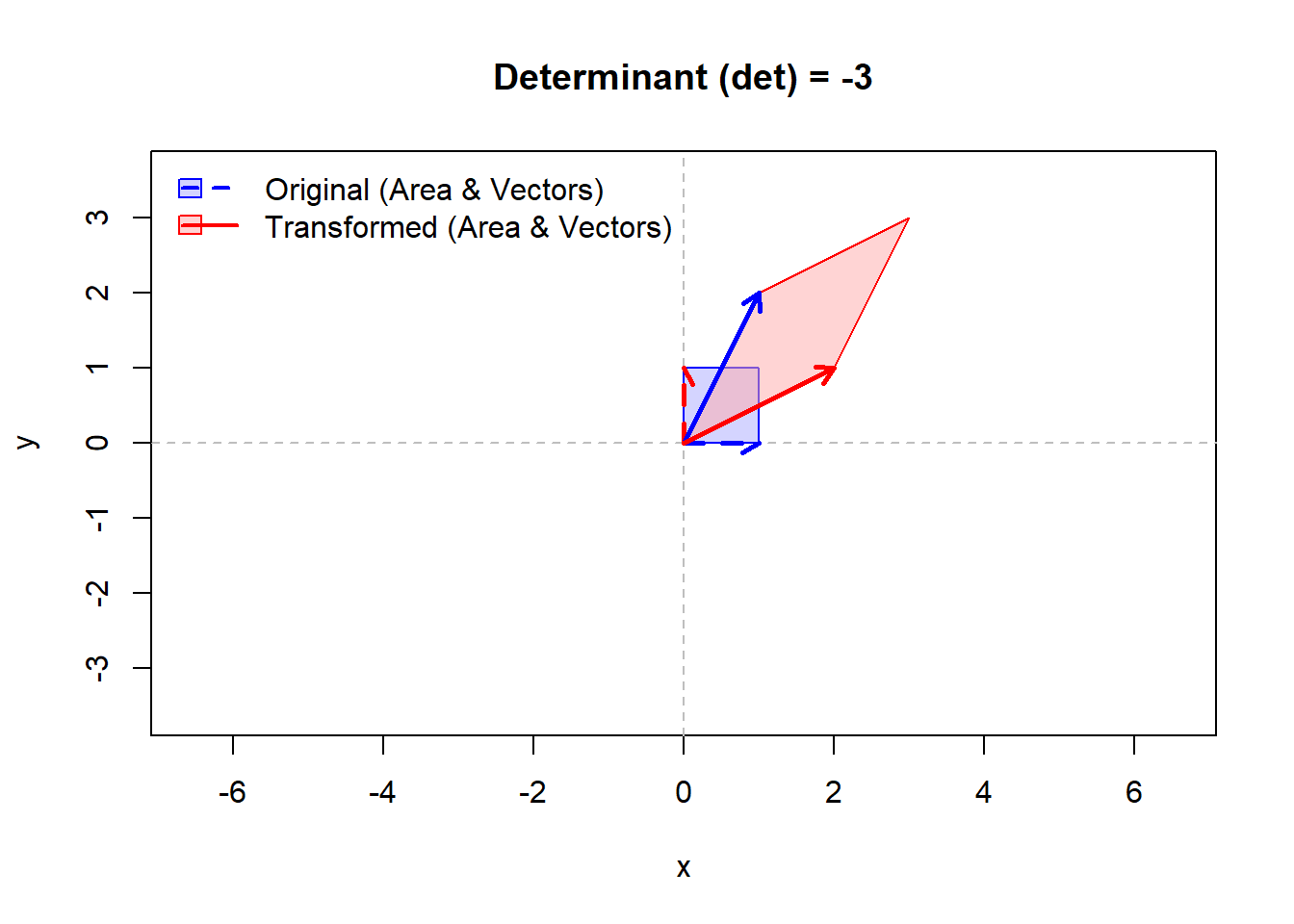
M2 <- matrix(c(1, 2, 2, 1), nrow = 2)
cat("\n行列 M2:\n")
print(M2)
cat("det(M2) =", det(M2), "(面積は3倍になるが、向きが反転します。Figure 2)\n")
plot_transform(M2)

# (c) 空間が潰れる (det = 0)
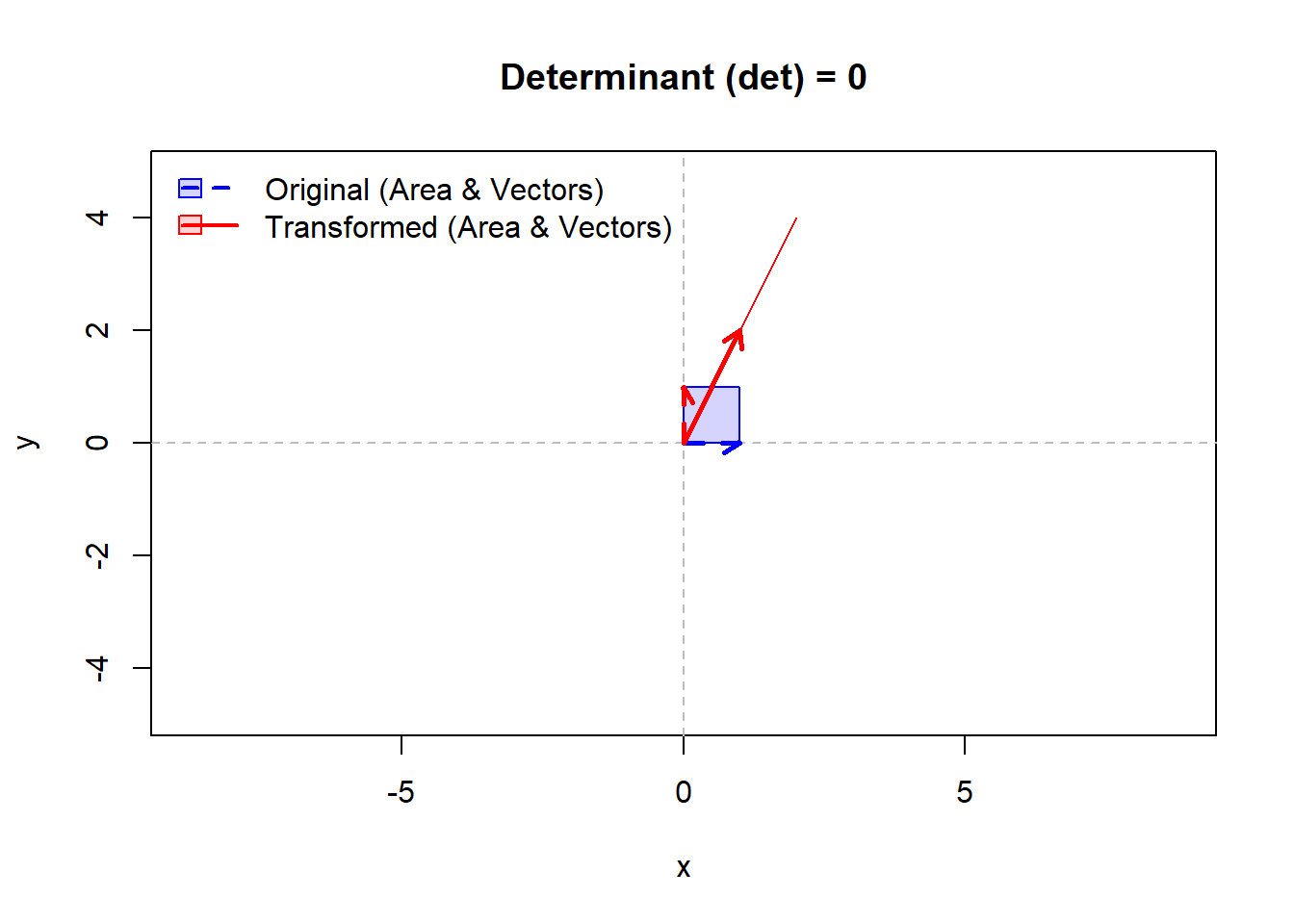
M3 <- matrix(c(1, 2, 1, 2), nrow = 2)
cat("\n行列 M3:\n")
print(M3)
cat("det(M3) =", det(M3), "(面積が0、つまり直線に潰れます。Figure 3)\n")
plot_transform(M3)


# --- シナリオ3: 性質の確認 det(AB) = det(A) * det(B) ---

cat("\n--- シナリオ3: 性質の確認 ---\n")

A <- matrix(c(2, 0, 1, 3), nrow = 2)
B <- matrix(c(1, 4, 0, 2), nrow = 2)
AB <- A %*% B

det_A <- det(A)
det_B <- det(B)
det_AB <- det(AB)
det_A_times_det_B <- det_A * det_B

cat("det(A) =", det_A, "\n")
cat("det(B) =", det_B, "\n")
cat("det(A) * det(B) =", det_A_times_det_B, "\n")
cat("det(A %*% B) =", det_AB, "\n")

cat("両者は一致するか？ ->", all.equal(det_AB, det_A_times_det_B), "\n")