Rで A/Bテスト:多腕バンディット問題 を試みます。
A/Bテストのシナリオは以下の通りです。
状況:
あるECサイトが、新しいキャンペーンのためにトップページに表示するバナー広告を作成しました。デザイン案が5つ(A, B, C, D, E)あり、どのデザインが最もクリックされやすい(=効果が高い)か分かりません。
目的:
サイトへのアクセスユーザーに5つのバナーのいずれかを表示し、そのクリック結果を学習します。テスト期間中、効果の低いバナーを延々と表示し続けることによる機会損失(得られたはずのクリックを逃すこと)を最小限に抑えつつ、最終的に最もクリック率(CTR)の高いバナーを見つけ出すことが目標です。
腕 (Arm):
5種類のバナーデザイン (Arm 1, Arm 2, Arm 3, Arm 4, Arm 5)
報酬 (Reward):
バナーがクリックされたら 1、クリックされなかったら 0。
試行回数 (Trials):
テスト期間中に合計 2,000 回のインプレッション(バナー表示機会)があるとします。
続いて A/Bテストに入ります。
本シミュレーションでは、「真のクリック率」を事前に設定しますが。アルゴリズムは、この真の確率を知らない状態で学習を進めます。
# 各バナー(腕)の真のクリック率を設定
# Arm 3が最も高い(0.15)が、アルゴリズムはこの事実を知らない
true_probs <- c(0.05, 0.08, 0.15, 0.11, 0.03)
arms <- length(true_probs)
trials <- 20003つの解法の実装と単一シミュレーション
a. ε-Greedy(イプシロン・グリーディ)法
確率 ε でランダムに探索し、それ以外は現在最も成績の良い腕を活用します。
# ε-Greedy 法の実装
epsilon_greedy <- function(true_probs, trials, epsilon = 0.1) {
arms <- length(true_probs)
counts <- rep(0, arms) # 各腕を引いた回数
values <- rep(0, arms) # 各腕の報酬の合計
total_reward <- 0
rewards_history <- numeric(trials) # 試行ごとの累積報酬を記録
for (t in 1:trials) {
if (runif(n = 1, min = 0, max = 1) < epsilon) {
# 探索(Exploration): ランダムに腕を選ぶ
chosen_arm <- sample(1:arms, 1)
} else {
# 活用(Exploitation): 現時点で平均報酬が最大の腕を選ぶ
# 平均が0の場合や同率一位がある場合も考慮し、ランダムに一つ選ぶ
avg_values <- ifelse(counts > 0, values / counts, 0)
best_arms <- which(avg_values == max(avg_values))
chosen_arm <- sample(best_arms, 1)
}
# 選んだ腕で報酬を得る (ベルヌーイ試行)
reward <- rbinom(1, 1, prob = true_probs[chosen_arm])
# 結果を更新
counts[chosen_arm] <- counts[chosen_arm] + 1
values[chosen_arm] <- values[chosen_arm] + reward
total_reward <- total_reward + reward
rewards_history[t] <- total_reward
}
return(list(total_reward = total_reward, rewards_history = rewards_history, counts = counts))
}b. UCB(Upper Confidence Bound)アルゴリズム
「平均報酬」と「不確かさ(試行回数が少ないほど大きい)」を足し合わせたUCBスコアが最も高い腕を選びます。
# UCB 法の実装
ucb <- function(true_probs, trials, c_param = 2) {
arms <- length(true_probs)
counts <- rep(0, arms)
values <- rep(0, arms)
total_reward <- 0
rewards_history <- numeric(trials)
# 最初に各腕を1回ずつ試す
for (i in 1:arms) {
reward <- rbinom(1, 1, prob = true_probs[i])
counts[i] <- 1
values[i] <- reward
total_reward <- total_reward + reward
rewards_history[i] <- total_reward
}
for (t in (arms + 1):trials) {
avg_values <- values / counts
# UCBスコアを計算
ucb_scores <- avg_values + sqrt(c_param * log(t) / counts)
# UCBスコアが最大の腕を選ぶ
best_arms <- which(ucb_scores == max(ucb_scores))
chosen_arm <- sample(best_arms, 1)
# 報酬を得て更新
reward <- rbinom(1, 1, prob = true_probs[chosen_arm])
counts[chosen_arm] <- counts[chosen_arm] + 1
values[chosen_arm] <- values[chosen_arm] + reward
total_reward <- total_reward + reward
rewards_history[t] <- total_reward
}
return(list(total_reward = total_reward, rewards_history = rewards_history, counts = counts))
}c. トンプソンサンプリング
各腕のクリック率をベータ分布でモデル化し、その分布からサンプリングした値が最も高い腕を選びます。
# トンプソンサンプリングの実装
thompson_sampling <- function(true_probs, trials) {
arms <- length(true_probs)
# ベータ分布のパラメータ (alpha:成功+1, beta:失敗+1)
alpha <- rep(1, arms)
beta <- rep(1, arms)
total_reward <- 0
rewards_history <- numeric(trials)
for (t in 1:trials) {
# 各腕の現在のベータ分布から値をサンプリング
sampled_probs <- rbeta(arms, alpha, beta)
# サンプル値が最大の腕を選ぶ
best_arms <- which(sampled_probs == max(sampled_probs))
chosen_arm <- sample(best_arms, 1)
# 報酬を得る
reward <- rbinom(1, 1, prob = true_probs[chosen_arm])
# ベータ分布のパラメータを更新
if (reward == 1) {
alpha[chosen_arm] <- alpha[chosen_arm] + 1
} else {
beta[chosen_arm] <- beta[chosen_arm] + 1
}
total_reward <- total_reward + reward
rewards_history[t] <- total_reward
}
return(list(total_reward = total_reward, rewards_history = rewards_history, counts = alpha + beta - 2))
}大規模シミュレーションの実行
次に、アルゴリズムの性能を安定して評価するために、このA/Bテストのシナリオを100回繰り返します。 さらに、シナリオの変数を変化させ、2つの異なる状況で比較します。
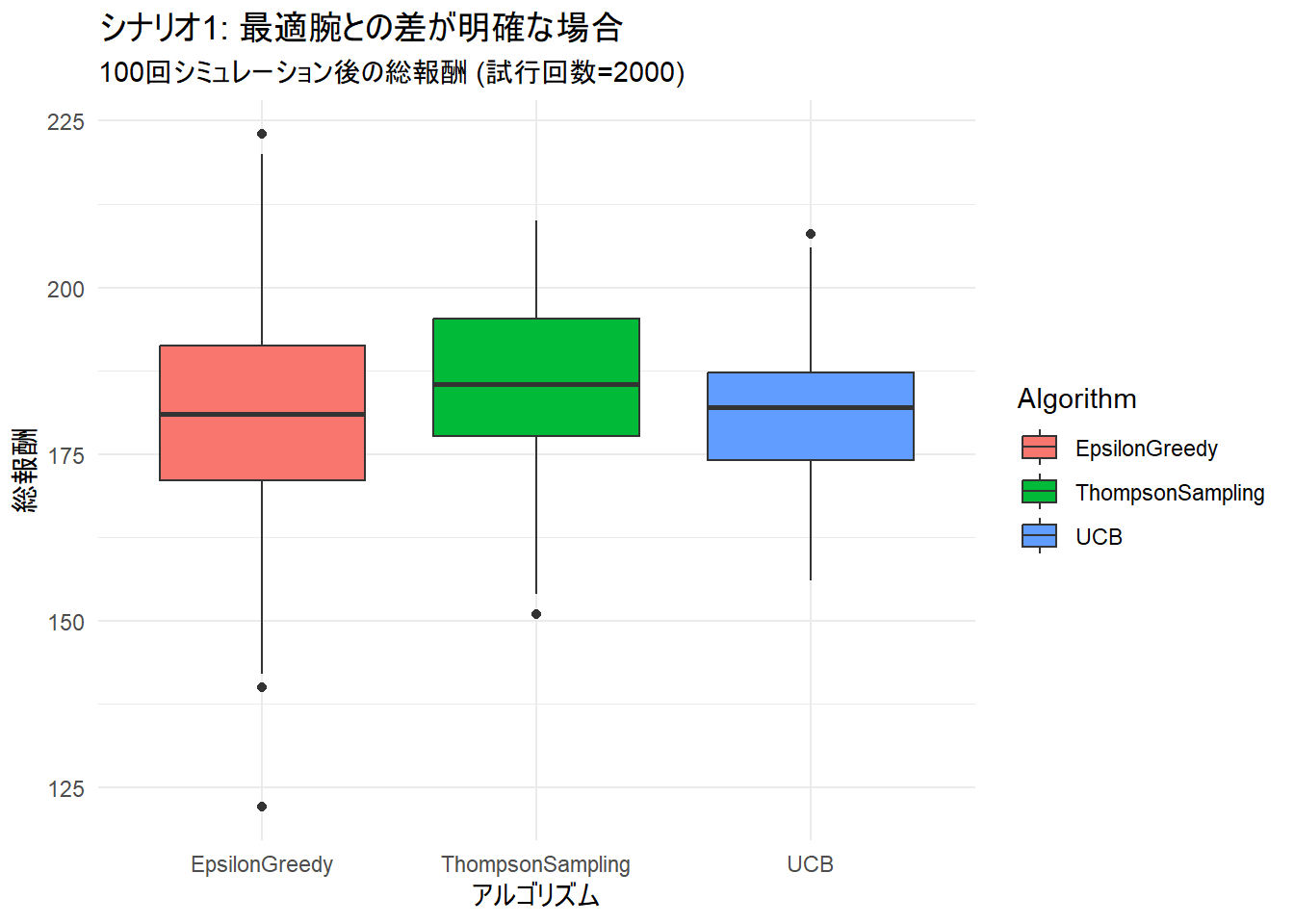
- シナリオ1: 最適な腕と他の腕の差が「明確」な場合
true_probs = c(0.05, 0.08, 0.15, 0.11, 0.03)
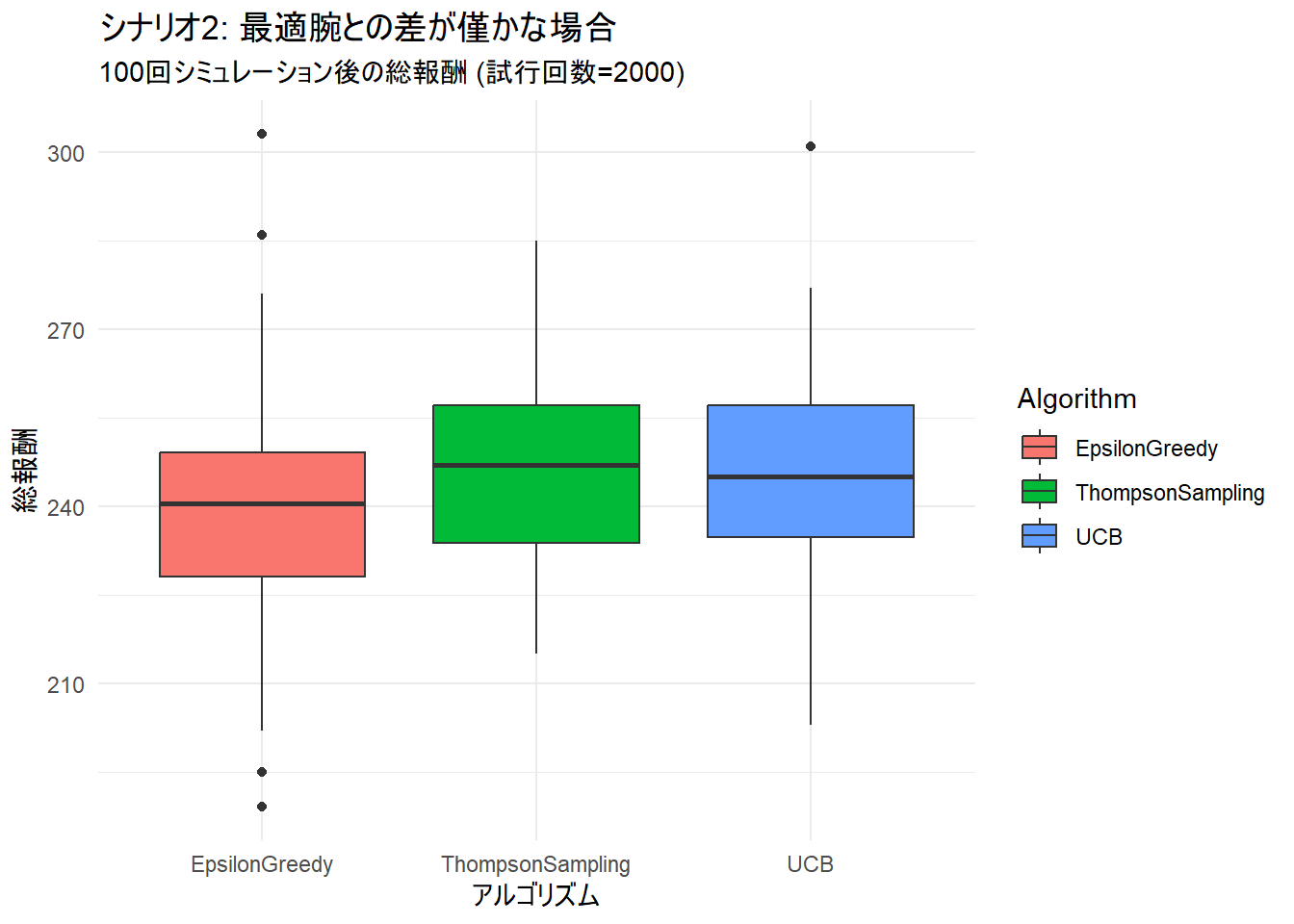
- シナリオ2: 最適な腕と他の腕の差が「僅か」な場合
true_probs_hard = c(0.10, 0.12, 0.15, 0.14, 0.09)
# シミュレーション設定
num_simulations <- 100
# シナリオ1: 差が明確な場合
true_probs_easy <- c(0.05, 0.08, 0.15, 0.11, 0.03)
# シナリオ2: 差が僅かな場合
true_probs_hard <- c(0.10, 0.12, 0.15, 0.14, 0.09)
# シミュレーション実行関数
run_simulations <- function(probs) {
# replicateを使って各アルゴリズムを100回実行
results_greedy <- replicate(num_simulations, epsilon_greedy(probs, trials)$total_reward, simplify = FALSE)
results_ucb <- replicate(num_simulations, ucb(probs, trials)$total_reward, simplify = FALSE)
results_ts <- replicate(num_simulations, thompson_sampling(probs, trials)$total_reward, simplify = FALSE)
# 結果をデータフレームにまとめる
results_df <- data.frame(
Simulation = 1:num_simulations,
EpsilonGreedy = unlist(results_greedy),
UCB = unlist(results_ucb),
ThompsonSampling = unlist(results_ts)
)
return(results_df)
}
seed <- 20250615
set.seed(seed)
# 各シナリオでシミュレーションを実行
results_easy_df <- run_simulations(true_probs_easy)
results_hard_df <- run_simulations(true_probs_hard)3つの解法の平均報酬の比較
最後に、100回のシミュレーション結果から平均報酬を算出し、比較・考察します。
比較結果の表示
library(dplyr)
# 平均総報酬を計算
avg_rewards_easy <- results_easy_df %>%
summarise(across(c(EpsilonGreedy, UCB, ThompsonSampling), mean))
avg_rewards_hard <- results_hard_df %>%
summarise(across(c(EpsilonGreedy, UCB, ThompsonSampling), mean))
cat("\n--- シナリオ1 (差が明確な場合) の平均総報酬 ---\n")
print(avg_rewards_easy)
cat("\n--- シナリオ2 (差が僅かな場合) の平均総報酬 ---\n")
print(avg_rewards_hard)
--- シナリオ1 (差が明確な場合) の平均総報酬 ---
EpsilonGreedy UCB ThompsonSampling
1 180.68 181.14 185.54
--- シナリオ2 (差が僅かな場合) の平均総報酬 ---
EpsilonGreedy UCB ThompsonSampling
1 239.16 245.13 245.78- 両ナリオにおいて、トンプソンサンプリングが最も高い平均報酬を達成しました。
- 同じく両シナリオにおいて ε-Greedy法 が最も劣った結果になりました。
結果の可視化と比較
library(ggplot2)
# データを整形
plot_data_easy <- results_easy_df %>%
tidyr::pivot_longer(cols = -Simulation, names_to = "Algorithm", values_to = "TotalReward")
plot_data_hard <- results_hard_df %>%
tidyr::pivot_longer(cols = -Simulation, names_to = "Algorithm", values_to = "TotalReward")
# シナリオ1のプロット
ggplot(plot_data_easy, aes(x = Algorithm, y = TotalReward, fill = Algorithm)) +
geom_boxplot() +
labs(
title = "シナリオ1: 最適腕との差が明確な場合",
subtitle = paste("100回シミュレーション後の総報酬 (試行回数=", trials, ")", sep = ""),
x = "アルゴリズム",
y = "総報酬"
) +
theme_minimal()
# シナリオ2のプロット
ggplot(plot_data_hard, aes(x = Algorithm, y = TotalReward, fill = Algorithm)) +
geom_boxplot() +
labs(
title = "シナリオ2: 最適腕との差が僅かな場合",
subtitle = paste("100回シミュレーション後の総報酬 (試行回数=", trials, ")", sep = ""),
x = "アルゴリズム",
y = "総報酬"
) +
theme_minimal()以上です。