Rで インパルス応答における変数順序の重要性 を確認します。
インパルス応答分析は、VARモデルのある変数にショック(予測誤差)が生じた場合、それが他の変数にどのような影響を及ぼすかを時系列で追跡する手法です。この分析には主に「直交化インパルス応答(OIRF)」と「一般化インパルス応答(GIRF)」の2種類があり、内生変数の順序に対する扱いが根本的に異なります。
このシミュレーションを通して、その違いを理論と実践の両面から確認します。
1. 理論的背景:なぜ変数の順序が影響するのか?
VARモデルと誤差項の相関
まず、基本的なVAR(p)モデルを考えます。
\(Y_t = c + A_1 Y_{t-1} + \dots + A_p Y_{t-p} + u_t\)
ここで、\(Y_t\)は内生変数のベクトル、\(A_i\)は係数行列、\(u_t\)は誤差項(ショック)のベクトルです。インパルス応答分析の目的は、この\(u_t\)の要素(例:\(u_{1t}\))に1単位のショックを与え、その影響が将来の\(Y_{t+h}\)にどう伝播するかを見ることです。
問題は、誤差項ベクトル\(u_t\)の各要素が互いに相関しているのが一般的である点です。例えば、2変数モデルで金融政策変数(金利)と物価変数がある場合、金利への予期せぬショックと物価への予期せぬショックは、同時点で相関している可能性があります。この相関をどう扱うかが、OIRFとGIRFの大きな違いとなります。
直交化インパルス応答 (OIRF): 変数順序に「依存する」理由
OIRFは、相関のある誤差項\(u_t\)を、互いに無相関な(=直交する)構造的ショック\(\epsilon_t\)に分解してから分析を行います。この分解に最も一般的に用いられるのがコレスキー分解です。
誤差項の共分散行列を\(\Sigma\)とすると、コレスキー分解は\(\Sigma = PP'\)となるような下三角行列\(P\)を見つけます。これを用いて、\(u_t = P\epsilon_t\)と関係づけます。
具体例(2変数モデル) 変数の順序を (y1, y2) とした場合、関係式は以下のようになります。
\(u_{1t} = p_{11}\epsilon_{1t}\)
\(u_{2t} = p_{21}\epsilon_{1t} + p_{22}\epsilon_{2t}\)
この式が意味することは、
-
y1への構造的ショック(\(\epsilon_{1t}\))は、同時点ではy1の誤差(\(u_{1t}\))にのみ影響する。 -
y2への構造的ショック(\(\epsilon_{2t}\))の影響を考える際、その前提としてy1へのショック(\(\epsilon_{1t}\))がy2の誤差(\(u_{2t}\))に与える影響(\(p_{21}\epsilon_{1t}\))が先に考慮されます。
つまり、コレスキー分解は、変数の順序に基づいて「同時点の因果関係」に再帰的な構造を仮定します。
先に置かれた変数(y1)は、後に置かれた変数(y2)に同時点で影響を与えますが、その逆(y2がy1に同時点で影響を与える)はない、と仮定するわけです。
もし変数の順序を (y2, y1) に変更すると、今度はy2がy1に同時点で影響を与えるという、全く逆の因果関係を仮定することになります。
この仮定の違いが、インパルス応答の結果に直接的な影響を及ぼすのです。したがって、OIRFを用いる際は、経済理論などに基づいて慎重に変数の順序を決定する必要があります。
一般化インパルス応答 (GIRF): 変数順序に「依存しない」理由
GIRFは、誤差項を直交化するという強い仮定を置きません。その代わり、ある1つの変数(例:y_j)にショックが起きたと仮定し、その影響を他の誤差項との歴史的な相関関係をそのまま利用して計算します。
具体的には、y_jの誤差項\(u_{jt}\)に1標準偏差のショックが起きたときの、誤差項ベクトル\(u_t\)の条件付き期待値を考えます。
\(E[u_t | u_{jt} = \sqrt{\sigma_{jj}}]\)
ここで、\(\sigma_{jj}\)は\(u_{jt}\)の分散です。この期待値は、共分散行列\(\Sigma\)の情報を直接用いて計算されます。例えば、y_iの誤差項\(u_{it}\)の期待値は、\((\sigma_{ij}/\sigma_{jj}) \times \sqrt{\sigma_{jj}}\) となります。
この計算は、共分散行列\(\Sigma\)の要素(\(\sigma_{ij}\), \(\sigma_{jj}\))にのみ依存します。共分散行列の値は、データセット内で変数がどのような順序で並べられていても変わりません。したがって、GIRFの結果は変数の順序に依存しない、頑健なものとなります。
2. シミュレーションによる実証
それでは、実際にRを使ってシミュレーションを行い、上記の違いを確認しましょう。
ステップ1: パッケージの読み込みと共通サンプルデータの作成
まず、必要なパッケージを読み込み、シミュレーション用のデータを作成します。誤差項が相関するように、共分散行列の非対角成分を0以外に設定するのがポイントです。
library(vars)
library(MASS)
library(tidyverse)
library(patchwork)
seed <- 20250625
set.seed(seed)
# データ生成のパラメータ設定
n_obs <- 200 # サンプルサイズ
# 誤差項の共分散行列(非対角成分が0でないことが重要)
sigma <- matrix(c(
1.0, 0.6,
0.6, 1.0
), nrow = 2, ncol = 2)
# 2変量正規分布に従う誤差項を生成
errors <- mvrnorm(n = n_obs, mu = c(0, 0), Sigma = sigma)
u1 <- errors[, 1]
u2 <- errors[, 2]
# 2変数の時系列データをVAR(1)プロセスで生成
y1 <- numeric(n_obs)
y2 <- numeric(n_obs)
for (t in 2:n_obs) {
y1[t] <- 0.7 * y1[t - 1] + 0.2 * y2[t - 1] + u1[t]
y2[t] <- 0.1 * y1[t - 1] + 0.5 * y2[t - 1] + u2[t]
}
# データフレームにまとめる
common_data <- data.frame(y1 = y1, y2 = y2)ステップ2: 2つの異なる順序でVARモデルを推定
同じデータ common_data を使い、変数の順序だけを変えた2つのデータセットを作成し、それぞれでVARモデルを推定します。
# ケース1: 順序 (y1, y2)
data_order1 <- common_data[, c("y1", "y2")]
var_model1 <- VAR(data_order1, p = 1, type = "none")
# ケース2: 順序 (y2, y1)
data_order2 <- common_data[, c("y2", "y1")]
var_model2 <- VAR(data_order2, p = 1, type = "none")ステップ3: 直交化インパルス応答 (OIRF) の比較
2つのモデルでOIRFを計算し、結果のデータフレームを比較します。ここでは「y1へのショックがy2に与える影響」に注目します。
# OIRFの計算 (ortho = TRUE)
oirf1 <- irf(var_model1, impulse = "y1", response = "y2", n.ahead = 20, ortho = TRUE, boot = FALSE)
oirf2 <- irf(var_model2, impulse = "y1", response = "y2", n.ahead = 20, ortho = TRUE, boot = FALSE)
# 結果のデータフレームを作成して比較
oirf_results <- data.frame(
period = 1:21,
order_y1_y2 = oirf1$irf$y1[, 1],
order_y2_y1 = oirf2$irf$y1[, 1]
)
cat("--- 直交化インパルス応答(OIRF)の結果比較 ---\n")
print(head(oirf_results))
# 2つの結果が異なることを確認
cat("\n2つの結果は同じか? ->", all.equal(oirf_results$order_y1_y2, oirf_results$order_y2_y1))--- 直交化インパルス応答(OIRF)の結果比較 ---
period order_y1_y2 order_y2_y1
1 1 0.6490847 0.00000000
2 2 0.4351377 0.05195748
3 3 0.2996102 0.06358334
4 4 0.2105219 0.05916814
5 5 0.1501270 0.04959361
6 6 0.1081834 0.03946091
2つの結果は同じか? -> Mean relative difference: 0.8211301実行結果:
データフレームを見ると、変数の順序を変えただけで、y1へのショックがy2に与える応答(order_y1_y2とorder_y2_y1)が全く異なる値になっていることが明確にわかります。
これは、コレスキー分解の前提となる「同時点の因果関係」の仮定が、順序によって変わってしまったためです。
ステップ4: 一般化インパルス応答 (GIRF) の比較
次に、GIRFで同じことを行います。
# GIRFの計算 (ortho = FALSE)
girf1 <- irf(var_model1, impulse = "y1", response = "y2", n.ahead = 20, ortho = FALSE, boot = FALSE)
girf2 <- irf(var_model2, impulse = "y1", response = "y2", n.ahead = 20, ortho = FALSE, boot = FALSE)
# 結果のデータフレームを作成して比較
girf_results <- data.frame(
period = 1:21,
order_y1_y2 = girf1$irf$y1[, 1],
order_y2_y1 = girf2$irf$y1[, 1]
)
cat("\n--- 一般化インパルス応答(GIRF)の結果比較 ---\n")
print(head(girf_results))
# 2つの結果が同じであることを確認
cat("\n2つの結果は同じか? ->", all.equal(girf_results$order_y1_y2, girf_results$order_y2_y1))
--- 一般化インパルス応答(GIRF)の結果比較 ---
period order_y1_y2 order_y2_y1
1 1 0.00000000 0.00000000
2 2 0.06251525 0.06251525
3 3 0.07650349 0.07650349
4 4 0.07119111 0.07119111
5 5 0.05967105 0.05967105
6 6 0.04747937 0.04747937
2つの結果は同じか? -> TRUEGIRFでは、変数の順序を変えても、応答結果が完全に一致していることがわかります。GIRFは変数の順序という分析者の恣意的な選択に影響されない、より頑健な手法であることが確認できました。
3. ggplotによる結果の可視化
最後に、この違いをグラフで視覚的に確認します。
グラフ描画用のデータ準備
# OIRFとGIRFの全結果を一つのデータフレームにまとめる
# 信頼区間も取得するためにboot = TRUEで再計算
oirf1_plot <- irf(var_model1, n.ahead = 20, ortho = TRUE, boot = TRUE, seed = 123)
oirf2_plot <- irf(var_model2, n.ahead = 20, ortho = TRUE, boot = TRUE, seed = 123)
girf1_plot <- irf(var_model1, n.ahead = 20, ortho = FALSE, boot = TRUE, seed = 123)
girf2_plot <- irf(var_model2, n.ahead = 20, ortho = FALSE, boot = TRUE, seed = 123)
# プロット用の関数
create_plot_df <- function(irf_obj, order_name) {
plot_df <- tibble()
for (imp in names(irf_obj$irf)) {
for (res in colnames(irf_obj$irf[[imp]])) {
df <- tibble(
impulse = imp,
response = res,
period = 0:20,
value = irf_obj$irf[[imp]][, res],
lower = irf_obj$Lower[[imp]][, res],
upper = irf_obj$Upper[[imp]][, res],
order = order_name
)
plot_df <- bind_rows(plot_df, df)
}
}
return(plot_df)
}
# データフレームの作成
oirf_plot_data <- bind_rows(
create_plot_df(oirf1_plot, "Order: y1, y2"),
create_plot_df(oirf2_plot, "Order: y2, y1")
)
girf_plot_data <- bind_rows(
create_plot_df(girf1_plot, "Order: y1, y2"),
create_plot_df(girf2_plot, "Order: y2, y1")
)直交化インパルス応答 (OIRF) のグラフ
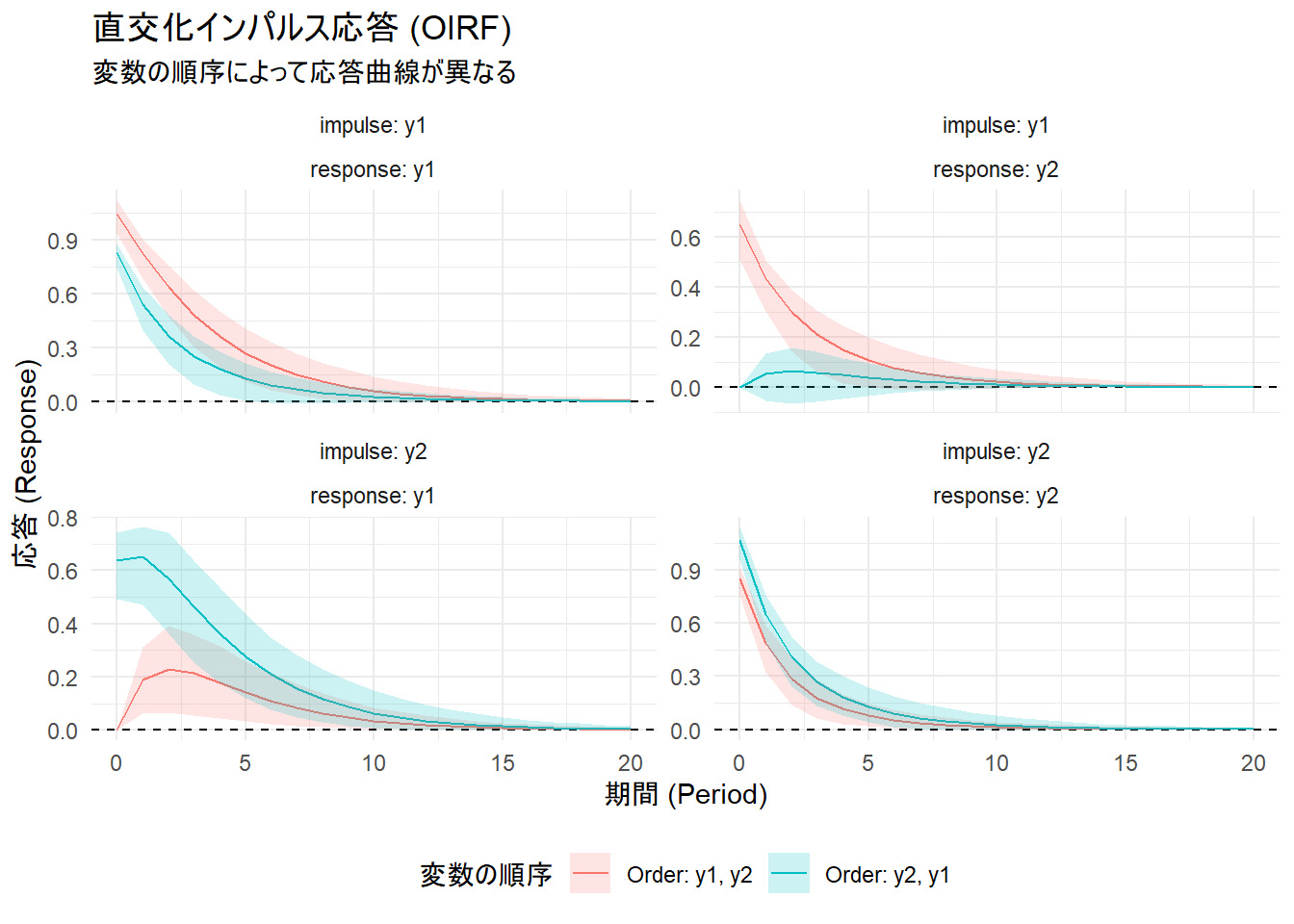
p_oirf <- ggplot(oirf_plot_data, aes(x = period, y = value, color = order, fill = order)) +
geom_hline(yintercept = 0, linetype = "dashed") +
geom_line() +
geom_ribbon(aes(ymin = lower, ymax = upper), alpha = 0.2, linetype = 0) +
facet_wrap(~ impulse + response, labeller = "label_both", scales = "free_y") +
labs(
title = "直交化インパルス応答 (OIRF)",
subtitle = "変数の順序によって応答曲線が異なる",
x = "期間 (Period)",
y = "応答 (Response)",
color = "変数の順序",
fill = "変数の順序"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(p_oirf)グラフから一目瞭然なように、変数の順序(Order: y1, y2 と Order: y2, y1)によって応答曲線が異なっています。特に「y1へのショックがy2に与える影響(impulse: y1, response: y2)」と「y2へのショックがy1に与える影響(impulse: y2, response: y1)」で、その違いが顕著です。
一般化インパルス応答 (GIRF) のグラフ
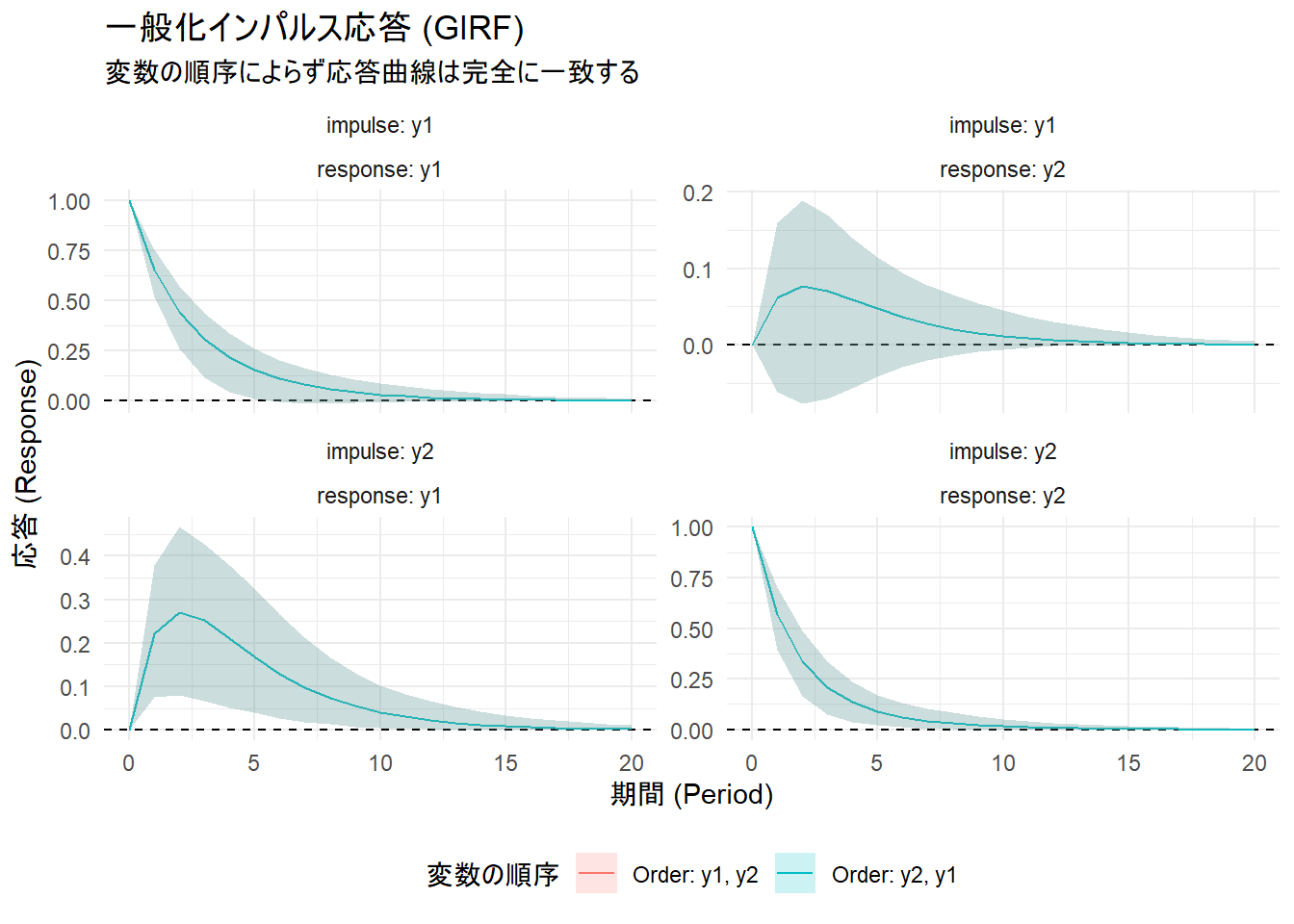
p_girf <- ggplot(girf_plot_data, aes(x = period, y = value, color = order, fill = order)) +
geom_hline(yintercept = 0, linetype = "dashed") +
geom_line() +
geom_ribbon(aes(ymin = lower, ymax = upper), alpha = 0.2, linetype = 0) +
facet_wrap(~ impulse + response, labeller = "label_both", scales = "free_y") +
labs(
title = "一般化インパルス応答 (GIRF)",
subtitle = "変数の順序によらず応答曲線は完全に一致する",
x = "期間 (Period)",
y = "応答 (Response)",
color = "変数の順序",
fill = "変数の順序"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(p_girf)一方、GIRFのグラフでは、2本の線(と信頼区間のリボン)が完全に重なっています。これは、GIRFが変数の順序という分析者の仮定に依存しないことを視覚的に示しています。
結論
本シミュレーションを通して、以下の点が確認できました。
直交化インパルス応答 (OIRF) は、誤差項を直交化するためにコレスキー分解を用います。この手法は変数間の同時点の因果関係について強い仮定を置くため、結果は変数の順序に大きく依存します。したがって、OIRFを用いる際には、経済理論等に基づいた慎重な順序決定が不可欠です。
一般化インパルス応答 (GIRF) は、誤差項の相関構造をそのまま利用してショックの影響を計算します。これにより、分析者が恣意的な仮定を置く必要がなく、結果は変数の順序に依存しません。そのため、特定の経済理論的な制約を課したくない場合や、頑健な結果を求めたい場合に非常に有用な手法です。
以上です。