Rでトービット･モデル

Rで トービット･モデル（Tobit Model） を試みます。

シナリオ：消費支出の調査と所得の影響

背景ストーリー

経済調査において、高級ワインへの年間支出額を調べています。調査対象者の中には、まったくワインを買わない人（支出額0）も多く含まれています。

一方で、年収が高い人ほど支出額は増える傾向があると考えられます。ただし、観測される支出額は 0以上の値しか取らず、負の値にはならないため、連続値の回帰モデル（OLS）では適切に扱えません。

トービット・モデルが適している理由

このように「従属変数が0以下に切り捨てられている（左側検閲されている）」場合、トービットモデルは観測されない支出意欲（潜在変数）に基づいて、ゼロの発生確率と正の支出額の分布を同時にモデル化できます。

シミュレーションと実装

ステップ 1: データ生成（支出額と年収）

seed <- 20250621
set.seed(seed)

n <- 300
income <- rnorm(n, mean = 500, sd = 100)

beta_0 <- -500
beta_1 <- 1.0
sigma <- 10

latent_spend <- beta_0 + beta_1 * income + rnorm(n, sd = sigma)
spend <- ifelse(latent_spend > 0, latent_spend, 0)

data <- data.frame(spend = spend, income = income)

# 検閲数の確認
cat("--- 支出 = 0 の人の数:", sum(data$spend == 0), " ---\n")
cat("\n--- サンプルデータのサマリー ---\n")
summary(data)

--- 支出 = 0 の人の数: 143  ---

--- サンプルデータのサマリー ---
     spend             income     
 Min.   :  0.000   Min.   :248.1  
 1st Qu.:  0.000   1st Qu.:423.9  
 Median :  9.177   Median :504.1  
 Mean   : 45.720   Mean   :504.8  
 3rd Qu.: 84.371   3rd Qu.:580.0  
 Max.   :268.230   Max.   :785.6

ステップ 2: トービット・モデルの実装（対数尤度の最大化）

loglik_tobit <- function(par, y, x) {
  beta_0 <- par[1]
  beta_1 <- par[2]
  sigma <- exp(par[3]) # log_sigma から変換、常に正

  xb <- beta_0 + beta_1 * x
  z <- (0 - xb) / sigma
  uncensored <- y > 0
  censored <- y <= 0

  ll <- numeric(length(y))
  ll[uncensored] <- dnorm(y[uncensored], mean = xb[uncensored], sd = sigma, log = TRUE)
  ll[censored] <- pnorm(z[censored], log.p = TRUE)

  return(-sum(ll)) # 最小化のために負の対数尤度を返す
}

# 初期値と最適化
init <- c(beta_0, beta_1, log(sigma))

opt_result <- optim(
  par = init,
  fn = loglik_tobit,
  y = spend,
  x = income,
  method = "BFGS",
  hessian = TRUE,
  control = list(
    reltol = 1e-16,
    maxit = 10000,
    parscale = c(100, 1, 1),
    ndeps = rep(1e-8, 3)
  )
)

# パラメータ推定値
beta_tobit <- opt_result$par
beta_tobit["sigma"] <- exp(beta_tobit[3])
names(beta_tobit) <- c("beta_0", "beta_1", "log_sigma", "sigma")

cat("--- 実装による推定: ---\n")
beta_tobit

--- 実装による推定: ---
      beta_0       beta_1    log_sigma        sigma 
-486.8299226    0.9788748    2.2413624    9.4061375

beta_1が約1ですので、年収が1万円増えるごとに支出意欲（潜在変数）が1単位増えると推定されます。
beta_0が約-490ですので、年収が約490万円を下回ると、ワインに全く支出しない（=支出0になる）確率が高くなると推定されます。

(参考): AER パッケージとの比較

model_pkg <- AER::tobit(spend ~ income, left = 0, data = data)

cat("--- AER::tobit() による推定: ---\n")
summary(model_pkg)

--- AER::tobit() による推定: ---

Call:
AER::tobit(formula = spend ~ income, left = 0, data = data)

Observations:
         Total  Left-censored     Uncensored Right-censored 
           300            143            157              0 

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -486.82992    6.66356  -73.06   <2e-16 ***
income         0.97887    0.01141   85.75   <2e-16 ***
Log(scale)     2.24136    0.05618   39.90   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Scale: 9.406 

Gaussian distribution
Number of Newton-Raphson Iterations: 23 
Log-likelihood:  -586 on 3 Df
Wald-statistic:  7354 on 1 Df, p-value: < 2.22e-16

ステップ 3: OLSモデルによる推定

ols_model <- lm(spend ~ income, data = data)
cat("--- OLS による推定: ---\n")
summary(ols_model)

--- OLS による推定: ---

Call:
lm(formula = spend ~ income, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-48.709 -23.538  -2.539  17.843  89.912 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -220.98530    8.30391  -26.61   <2e-16 ***
income         0.52834    0.01612   32.78   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.8 on 298 degrees of freedom
Multiple R-squared:  0.7829,    Adjusted R-squared:  0.7822 
F-statistic:  1075 on 1 and 298 DF,  p-value: < 2.2e-16

ステップ 4: トービット･モデルとOLSモデルの比較

cat("--- 推定値の比較: ---\n")
cat("【真の値】\n")
cat("beta_0 =", beta_0, "\n")
cat("beta_1 =", beta_1, "\n\n")

cat("【OLS推定値】\n")
print(coef(ols_model))

cat("\n【トービット推定値】\n")
print(round(beta_tobit[c("beta_0", "beta_1")], 3))

--- 推定値の比較: ---
【真の値】
beta_0 = -500 
beta_1 = 1 

【OLS推定値】
(Intercept)      income 
-220.985296    0.528342 

【トービット推定値】
  beta_0   beta_1 
-486.830    0.979

library(ggplot2)

ggplot(data, aes(x = income, y = spend)) +
  geom_point(alpha = 0.4) +
  geom_abline(
    intercept = coef(ols_model)[1],
    slope = coef(ols_model)[2],
    color = "blue", linetype = "dashed"
  ) +
  geom_abline(
    intercept = beta_tobit["beta_0"],
    slope = beta_tobit["beta_1"],
    color = "red", linetype = "solid"
  ) +
  labs(
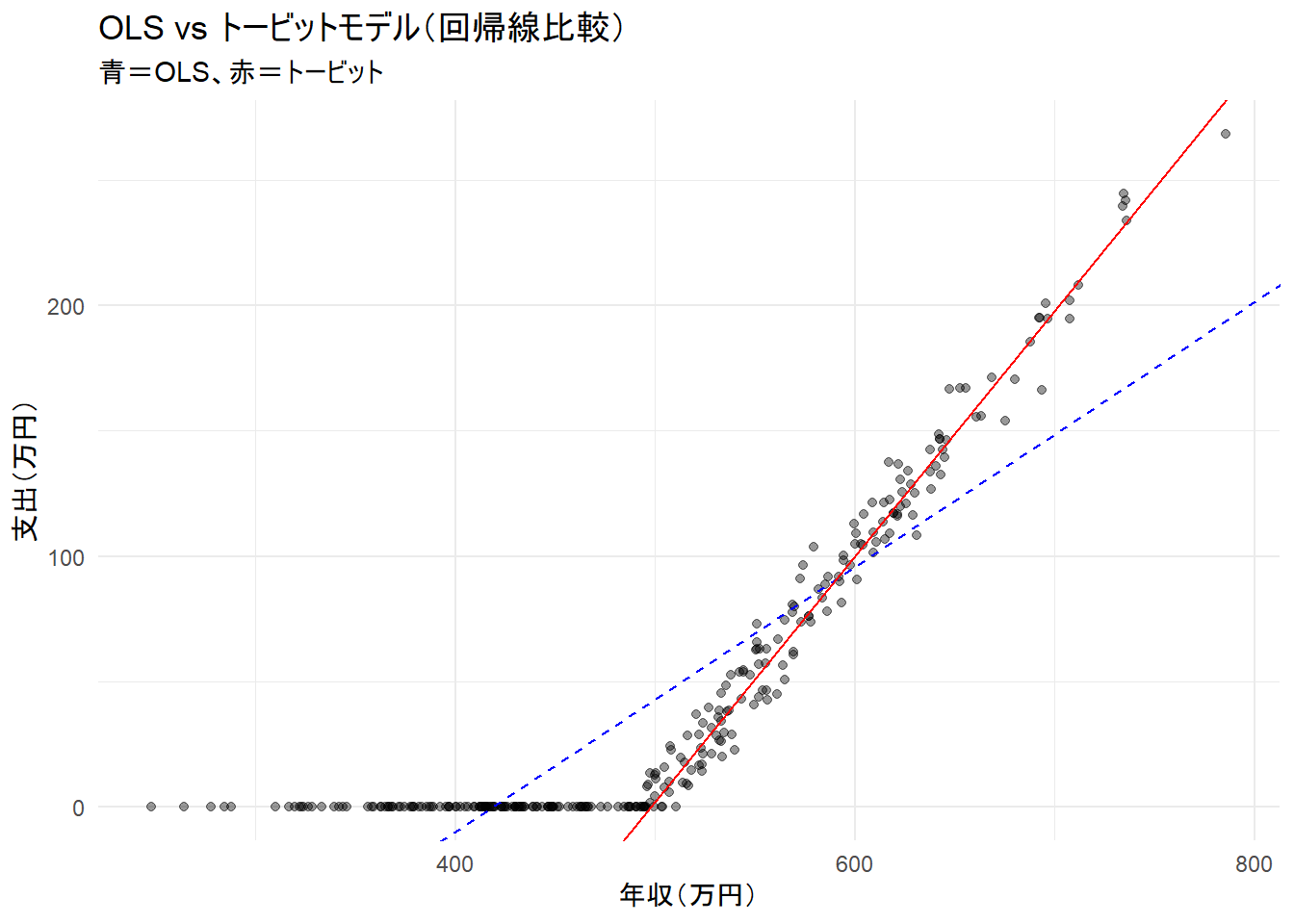
    title = "OLS vs トービットモデル（回帰線比較）",
    subtitle = "青＝OLS、赤＝トービット",
    x = "年収（万円）",
    y = "支出（万円）"
  ) +
  theme_minimal()

視点	OLS	トービットモデル
検閲の考慮	無視	明示的にモデル化
ゼロが多いと…	傾きが下方バイアス	正しく識別可能
切片	高めに出やすい（上方バイアス）	潜在変数の実態を反映
適用場面	完全連続な従属変数向き	切り捨てられた従属変数に適切

以上です。