Rで常時微動解析

library(ggplot2)

# シミュレーションのパラメータ設定
fs <- 100 # サンプリング周波数 (Hz)
duration <- 60 # データ長 (秒)
N <- fs * duration # データ点数
t <- seq(0, duration - 1 / fs, by = 1 / fs) # 時間軸

# 模擬する地盤の特性
f_peak <- 2.0 # 卓越振動数 (Hz)
T_peak <- 1 / f_peak # 卓越周期 (秒)

seed <- 20250625
set.seed(seed)


# 鉛直動 (UD) の生成: 単純なホワイトノイズ
ud_signal <- rnorm(N, mean = 0, sd = 1)

# 水平動 (NS, EW) の生成
# もとになるホワイトノイズを生成
base_noise_ns <- rnorm(N, mean = 0, sd = 1)
base_noise_ew <- rnorm(N, mean = 0, sd = 1)

# (2) 2Hzでピークを持つフィルタ（伝達関数）を周波数領域で作成
freq <- seq(0, fs, length.out = N) # 周波数軸

# ガウス型のフィルタを作成（まず正の周波数側のみ）
transfer_function <- exp(-(freq - f_peak)^2 / (2 * (f_peak * 0.2)^2))

# FFTの対称性を手動で構築します。
# 逆FFTした結果が実数になるためには、スペクトルが共役対称である必要があります。
# Nが偶数の場合、FFTの結果は次のような構成になっています。
# - index 1: DC成分 (0 Hz)
# - index 2 から N/2: 正の周波数成分
# - index N/2 + 1: ナイキスト周波数
# - index (N/2 + 2) から N: 負の周波数成分（正の成分の鏡像）
#
# 正の周波数成分 (index 2からN/2) を反転させて、負の周波数成分の位置にコピーします。
if (N %% 2 == 0) { # Nが偶数の場合
  transfer_function[(N / 2 + 2):N] <- rev(transfer_function[2:(N / 2)])
} else { # Nが奇数の場合（今回は該当しませんが、汎用性のために記述）
  transfer_function[((N + 1) / 2 + 1):N] <- rev(transfer_function[2:((N + 1) / 2)])
}

# (3) フィルタを適用
fft_ns <- fft(base_noise_ns)
fft_ew <- fft(base_noise_ew)

fft_ns_filtered <- fft_ns * transfer_function
fft_ew_filtered <- fft_ew * transfer_function

# (4) 逆フーリエ変換で時間領域の波形に戻す
ns_signal <- Re(fft(fft_ns_filtered, inverse = TRUE) / N)
ew_signal <- Re(fft(fft_ew_filtered, inverse = TRUE) / N)

# 生成した時系列データをデータフレームにまとめる
df_timeseries <- data.frame(
  time = t,
  NS = ns_signal,
  EW = ew_signal,
  UD = ud_signal
)

# 生成した波形の一部をプロットして確認
p1 <- ggplot(df_timeseries[1:(fs * 5), ], aes(x = time)) +
  geom_line(aes(y = NS, colour = "NS (水平)")) +
  geom_line(aes(y = EW, colour = "EW (水平)")) +
  geom_line(aes(y = UD, colour = "UD (鉛直)"), linetype = "dashed") +
  labs(
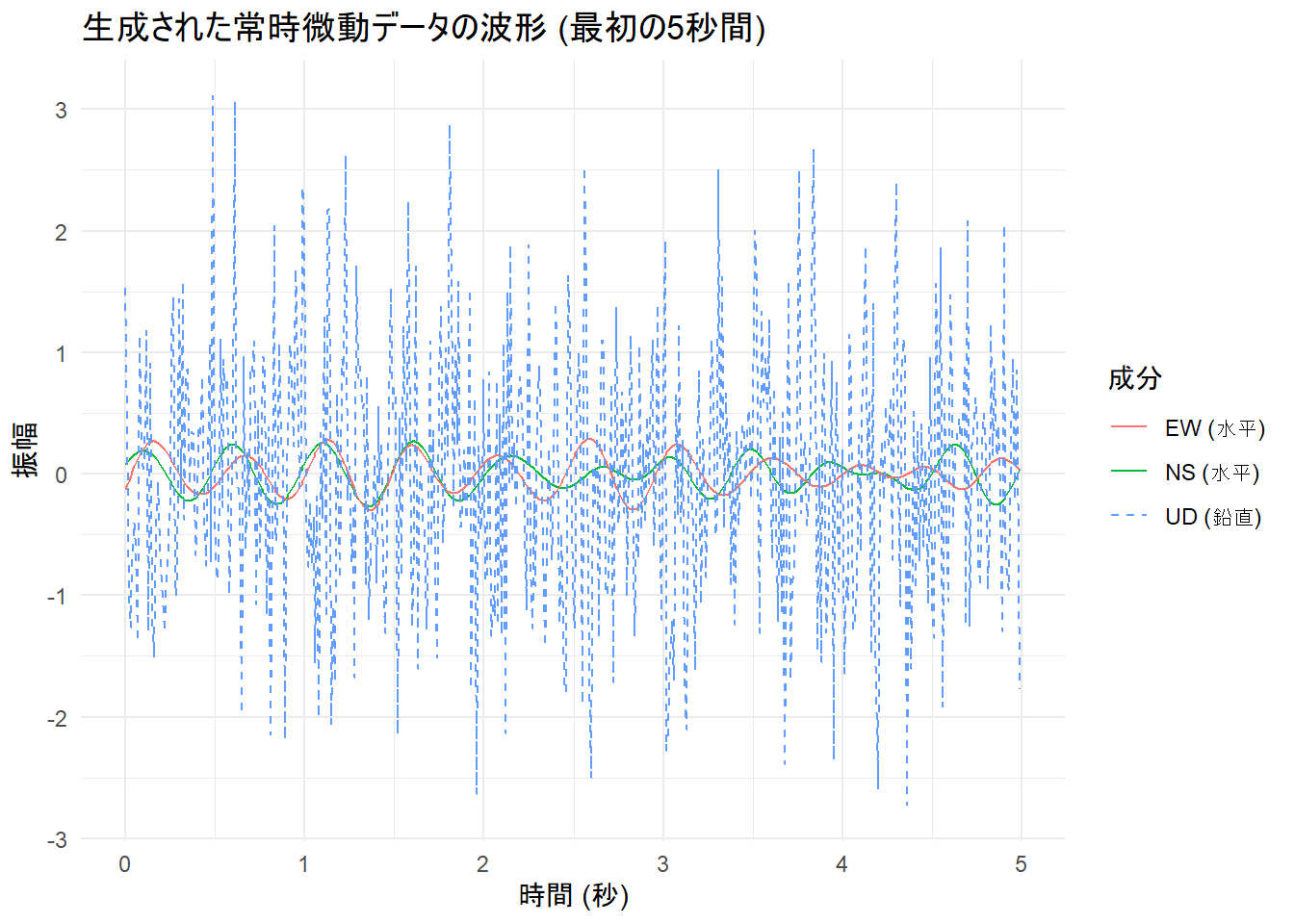
    title = "生成された常時微動データの波形 (最初の5秒間)",
    x = "時間 (秒)", y = "振幅", colour = "成分"
  ) +
  theme_minimal()
print(p1)

# 各成分をフーリエ変換してスペクトルを計算
spec_ns <- Mod(fft(ns_signal))
spec_ew <- Mod(fft(ew_signal))
spec_ud <- Mod(fft(ud_signal))

# 水平動スペクトル (H) を合成
spec_h <- sqrt(spec_ns^2 + spec_ew^2)

# 鉛直動スペクトル (V)
spec_v <- spec_ud

# H/Vスペクトル比を計算
hv_ratio <- spec_h / (spec_v + 1e-9)

# プロット用にデータフレームを作成 (片側スペクトルのみ)
df_hv <- data.frame(
  frequency = freq[1:(N / 2)],
  hv_ratio = hv_ratio[1:(N / 2)]
)

# H/Vスペクトル比をプロット
p2 <- ggplot(df_hv, aes(x = frequency, y = hv_ratio)) +
  geom_line() +
  geom_vline(xintercept = f_peak, color = "red", linetype = "dashed") +
  annotate("text",
    x = f_peak + 1, y = max(df_hv$hv_ratio) * 0.9,
    label = paste0("設定した卓越振動数 = ", f_peak, " Hz"), color = "red"
  ) +
  labs(
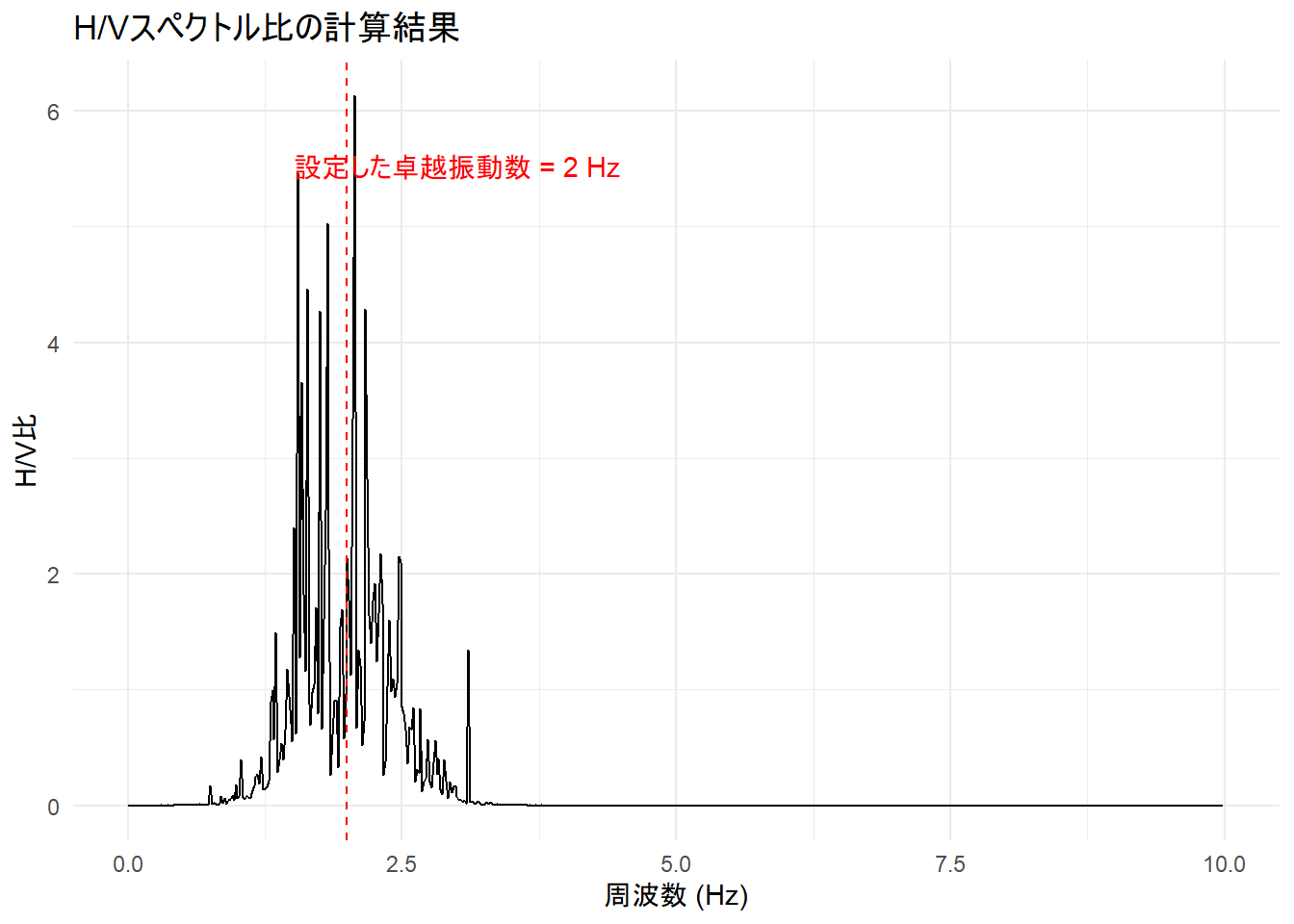
    title = "H/Vスペクトル比の計算結果",
    x = "周波数 (Hz)",
    y = "H/V比"
  ) +
  xlim(0, 10) + # 関心のある周波数範囲に絞る
  theme_minimal()
print(p2)