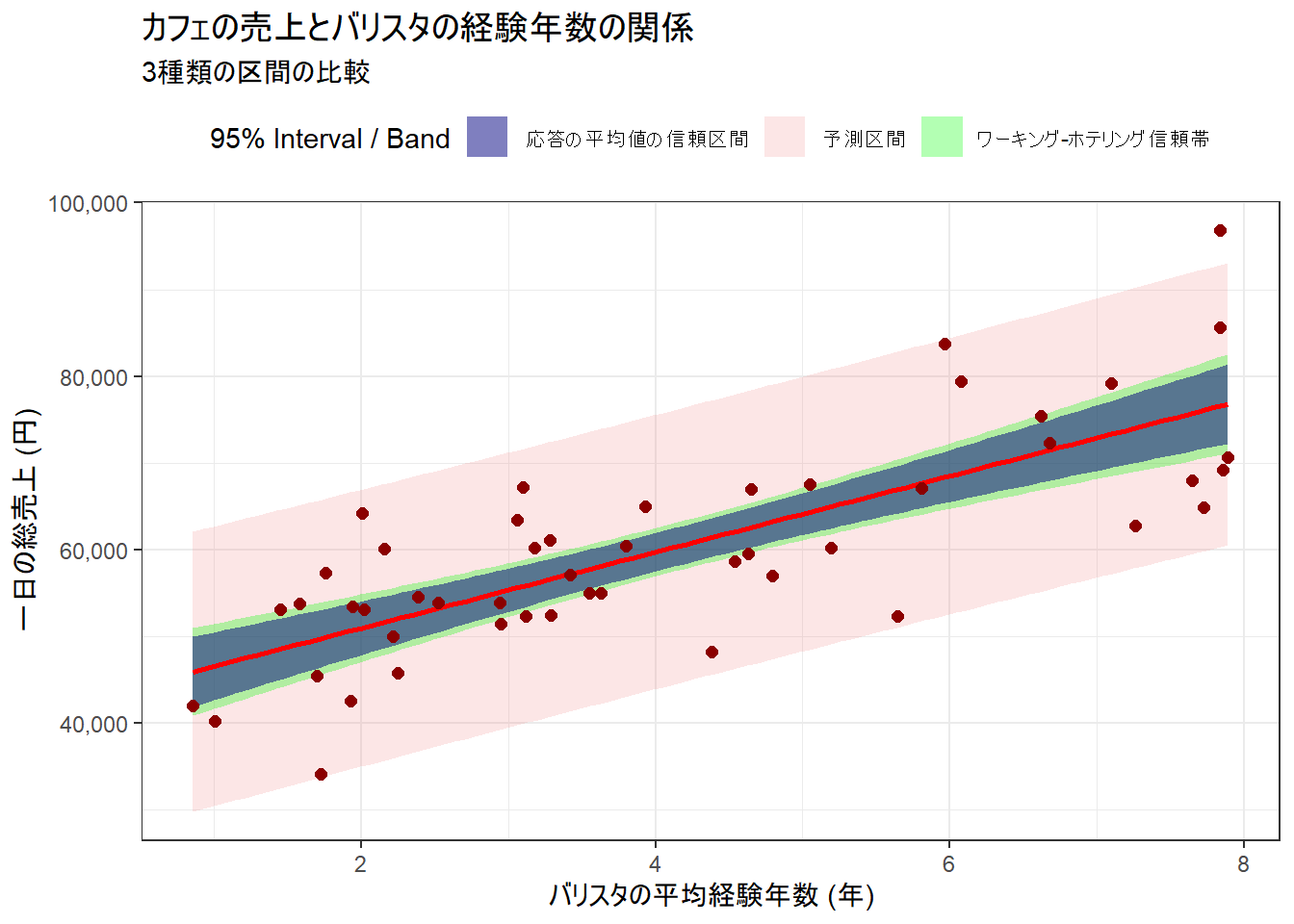
Rで 線形回帰における各種区間 を算出します。
1. 架空のストーリー:カフェの売上とバリスタの経験年数
シナリオ: あなたは、小さなカフェ「せんけいコーヒー」のオーナーです。最近、日々の売上にばらつきがあることに気づきました。あなたは「熟練したバリスタがシフトに入っている日ほど、売上が高いのではないか?」という仮説を立てました。
熟練したバリスタは、コーヒーを淹れるのが速いだけでなく、常連客との会話が弾んだり、新しい豆を上手におすすめしたりすることで、客単価や客数を向上させる可能性があるからです。
そこで、この仮説を検証するために、過去50日間のデータを記録しました。
- 説明変数 (x): その日にシフトに入ったバリスタたちの平均経験年数
- 目的変数 (y): その日の総売上(円)
このデータを使って、バリスタの経験年数が売上にどれほど影響を与えるのかを分析し、将来の売上を予測したいと考えています。
2. Rによるシミュレーションと区間の算出
library(ggplot2)
library(dplyr)
# === データ生成 (シナリオに基づいたシミュレーション) ===
seed <- 20250623
set.seed(seed)
# シナリオ設定
n <- 50 # データ収集日数
true_intercept <- 40000 # 経験0年のバリスタのみの場合の基礎売上 (4万円)
true_slope <- 5000 # 平均経験年数が1年増えるごとの売上増加額 (5千円)
error_sd <- 8000 # 日々のランダムな売上変動の標準偏差 (8千円)
# 架空のデータを生成
experience <- runif(n, 0.5, 8) # バリスタの平均経験年数を0.5年から8年の間でランダムに生成
true_sales <- true_intercept + true_slope * experience
sales <- true_sales + rnorm(n, mean = 0, sd = error_sd) # ランダムな誤差を加える
# データフレームにまとめる
cafe_data <- data.frame(experience, sales)
# === 線形回帰モデルの構築 ===
model <- lm(sales ~ experience, data = cafe_data)
model_summary <- summary(model)
# === 4つの区間の算出 ===
# 1. 母回帰係数(傾きと切片)の信頼区間
coef_ci <- confint(model, level = 0.95)
# 予測用のx軸データを生成 (グラフを滑らかにするため)
pred_grid <- data.frame(experience = seq(min(experience), max(experience), length.out = 100))
# 2. 応答の平均値の信頼区間 (t分布)
mean_conf_interval <- predict(model, newdata = pred_grid, interval = "confidence", level = 0.95) %>%
as.data.frame() %>%
rename(fit_conf = fit, lwr_conf = lwr, upr_conf = upr)
# 3. 目的変数の予測区間
pred_interval <- predict(model, newdata = pred_grid, interval = "prediction", level = 0.95) %>%
as.data.frame() %>%
rename(fit_pred = fit, lwr_pred = lwr, upr_pred = upr)
# 4. ワーキング-ホテリング信頼帯 (F分布)
f_value <- qf(0.95, 2, model$df.residual)
wh_multiplier <- sqrt(2 * f_value)
se_fit <- predict(model, newdata = pred_grid, se.fit = TRUE)$se.fit
wh_lwr <- mean_conf_interval$fit_conf - wh_multiplier * se_fit
wh_upr <- mean_conf_interval$fit_conf + wh_multiplier * se_fit
# グラフ描画用にすべてのデータを結合
plot_data <- bind_cols(pred_grid, mean_conf_interval, pred_interval) %>%
mutate(wh_lwr = wh_lwr, wh_upr = wh_upr)
# === ggplotによる可視化 ===
ggplot() +
# 予測区間 (一番外側・最も広い)
geom_ribbon(data = plot_data, aes(x = experience, ymin = lwr_pred, ymax = upr_pred, fill = "Prediction"), alpha = 0.2) +
# ワーキング-ホテリング信頼帯 (中間)
geom_ribbon(data = plot_data, aes(x = experience, ymin = wh_lwr, ymax = wh_upr, fill = "Working-Hotelling"), alpha = 0.3) +
# 応答の平均値の信頼区間 (一番内側・最も狭い)
geom_ribbon(data = plot_data, aes(x = experience, ymin = lwr_conf, ymax = upr_conf, fill = "Confidence"), alpha = 0.5) +
# 回帰直線
geom_line(data = plot_data, aes(x = experience, y = fit_conf), color = "red", linewidth = 1) +
# 元データの散布図
geom_point(data = cafe_data, aes(x = experience, y = sales), color = "darkred", size = 2) +
# ラベルとデザイン
scale_fill_manual(
name = "95% Interval / Band",
values = c("Prediction" = "lightcoral", "Working-Hotelling" = "green", "Confidence" = "navy"),
labels = c("応答の平均値の信頼区間", "予測区間", "ワーキング-ホテリング信頼帯")
# labels = c("Confidence (Mean)", "Prediction (New Day)", "W-H Band (Whole Line)")
) +
scale_y_continuous(labels = scales::comma) +
labs(
title = "カフェの売上とバリスタの経験年数の関係",
subtitle = "3種類の区間の比較",
x = "バリスタの平均経験年数 (年)",
y = "一日の総売上 (円)"
) +
theme_bw() +
theme(legend.position = "top")3. 各区間の算出結果とシナリオにおける解釈
1. 母回帰係数(傾きと切片)の信頼区間
算出結果:
coef_ci 2.5 % 97.5 %
(Intercept) 37377.970 46994.365
experience 3340.194 5433.254シナリオにおける解釈:
- 傾き (experience) について:信頼区間に0は含まれていないため、95%の信頼度で「バリスタの平均経験年数が1年増えるごとに、一日の総売上は 3,340円から5,433円の間で増加する 」、「バリスタの経験年数は売上に対して統計的に意味のあるプラスの影響を与えている」ことを示唆しています。
- 切片 (Intercept) について: 「もし仮に経験年数0年のバリスタだけで店を運営した場合、その日の平均的な売上は 37,378円から46,994円の間 になるだろう」と推定されます。これは、店の基本的な売上ポテンシャルを示しています。
2. 応答の平均値の信頼区間 (グラフの最も内側の帯)
シナリオにおける解釈:
- これは「特定の日ではなく、平均的に見ればどうなるか」を示します。 例えば、グラフの
experience = 5(平均経験5年のチーム)の点を確認した場合、「今後、平均経験5年のバリスタチームで営業する日を何日も繰り返した場合、それらの日の平均売上は、95%の信頼度で 61,705円〜66,535円 に収まるだろう」と解釈できます。
newdata_point <- data.frame(experience = 5)
predict(model, newdata = newdata_point, interval = "confidence", level = 0.95) fit lwr upr
1 64119.79 61704.52 66535.053. 目的変数の予測区間 (グラフの最も外側の帯)
シナリオにおける解釈:
これは「次の一回はどうなるか」という、具体的な予測です。 再び
experience = 5の点を確認しますと、「次の火曜日に、平均経験5年のバリスタチームで営業する場合、その一日の実際の売上は、95%の信頼度で 48,277円〜79,962円 に収まるだろう」と予測されます。なお、この区間が広いのは、「平均的な売上の不確実性」に加えて、「その日特有の不確実性(例えば、天気、客層など)」という個別の誤差も考慮しているためです。\(\hat{\sigma} \sqrt{\frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{xx}}}\) : モデルの不確実性(平均値の信頼区間の幅を決める部分)
\(\hat{\sigma} \sqrt{1}\) : 個別の誤差の不確実性(\(\hat{\sigma}\) そのもの)
newdata_point <- data.frame(experience = 5)
predict(model, newdata = newdata_point, interval = "prediction", level = 0.95) fit lwr upr
1 64119.79 48277.4 79962.174. ワーキング-ホテリング信頼帯 (グラフの中間の帯)
シナリオにおける解釈:
- 「『真の関係性』を表す直線そのものが、95%の信頼度で、この帯の中にまるごと全部収まっていると言える」と解釈します。個別の予測よりも、構築した回帰モデル全体の信頼性を評価するための区間です。ビジネス上の重要な意思決定(例:熟練バリスタを雇用するための新しい給与体系の導入)を行う際に、モデルそのものがどれほど信頼できるかの裏付けを与えてくれます。
4. 各区間の算出式
記号は以下のように定義します。
- \(\hat{\alpha}\): 標本から計算した傾き(回帰係数)
- \(\hat{\beta}\): 標本から計算した切片
- \(n\): サンプルサイズ
- \(x_0\): 予測したい説明変数の特定の値
- \(\bar{x}\): 説明変数 \(x\) の標本平均
- \(S_{xx}\): 説明変数 \(x\) の偏差平方和, \(\sum_{i=1}^{n}(x_i - \bar{x})^2\)
- \(\hat{\sigma}\): 残差標準誤差, \(\sqrt{\frac{\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}{n-2}}\)
- \(t_{\left(n-2, \frac{\alpha}{2}\right)}\): 自由度 \(n-2\) のt分布における上側 \(\frac{\alpha}{2}\) 点
- \(F_{\left(2, n-2, \alpha\right)}\): 第一自由度 2, 第二自由度 \(n-2\) のF分布における上側 \(\alpha\) 点
1. 母回帰係数の信頼区間 (Confidence Intervals for Regression Coefficients)
傾き \(\alpha\) の \((1-\alpha) \times 100\%\) 信頼区間:
\[\hat{\alpha} \pm t_{\left(n-2, \frac{\alpha}{2}\right)} \times \frac{\hat{\sigma}}{\sqrt{S_{xx}}}\]
切片 \(\beta\) の \((1-\alpha) \times 100\%\) 信頼区間:
\[\hat{\beta} \pm t_{\left(n-2, \frac{\alpha}{2}\right)} \times \hat{\sigma} \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{S_{xx}}}\]
2. 応答の平均値の信頼区間 (Confidence Interval for the Mean Response)
\(x=x_0\) における \(y\) の平均値 \(E[Y|X=x_0]\) の \((1-\alpha) \times 100\%\) 信頼区間:
\[\left(\hat{\alpha}x_0 + \hat{\beta}\right) \pm t_{\left(n-2, \frac{\alpha}{2}\right)} \times \hat{\sigma} \sqrt{\frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{xx}}}\]
3. 目的変数の予測区間 (Prediction Interval for a New Observation)
\(x=x_0\) における新しい観測値 \(y_0\) の \((1-\alpha) \times 100\%\) 予測区間:
\[\left(\hat{\alpha}x_0 + \hat{\beta}\right) \pm t_{\left(n-2, \frac{\alpha}{2}\right)} \times \hat{\sigma} \sqrt{1 + \frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{xx}}}\]
4. ワーキング-ホテリング信頼帯 (Working-Hotelling Confidence Band)
回帰直線全体 \(Y = \alpha X + \beta\) を覆う \((1-\alpha) \times 100\%\) 同時信頼帯:
\[\left(\hat{\alpha}x_0 + \hat{\beta}\right) \pm \sqrt{2 F_{\left(2, n-2, \alpha\right)}} \times \hat{\sigma} \sqrt{\frac{1}{n} + \frac{(x_0 - \bar{x})^2}{S_{xx}}}\]
5. 「95%信頼度」ついて
「95%信頼度」とは、「算出された特定の区間の中に真の値が存在する確率が95%である」、という意味ではありません。
真の値(例えば、母集団における真の傾き \(\alpha\))は、固定された一つの値であり、計算した特定の区間の中にあるか、ないかのどちらかです。確率的に変動するものではありません。
95%とは「区間を計算する、その手順(プロセス)の信頼性」に対するものであり、「もし、同じ方法で何度も(例えば100回)標本を抽出し、その都度同じ手順で信頼区間を計算したら、その100個の区間のうち約95個は、真の値を含むだろう」 と解釈される数字です。
つまり「95%の信頼度」は、手にした一つの結果が正しい確率を示すものではなく、その結果を導き出した「統計的手法」が、長期的に見てどれだけ信頼できるかを示す指標です。
各区間における「95%信頼度」
母回帰係数の信頼区間
- 対象: 傾き \(\alpha\) と切片 \(\beta\) という、固定された未知のパラメータ。
- 95%信頼度の意味(傾きの場合): 「もし、このカフェで何度も(例えば100回)独立に50日間のデータを収集し直し、その都度、傾きの信頼区間を計算すれば、その100個の区間のうち約95個は、“真の傾き”(経験年数が1年増えたときの、本当の売上増加額)を含むことになる。」
応答の平均値の信頼区間
- 対象: 特定の \(x_0\) における Yの平均値 \(E[Y|X=x_0]\) という、固定された未知のパラメータ。
- 95%信頼度の意味(経験5年の場合): 「もし、何度も50日間のデータを収集し直し、その都度『経験5年のバリスタチームにおける平均売上』の信頼区間を計算すれば、その区間のうち約95個は、“真の平均売上” を含むことになる。」
目的変数の予測区間
- 対象: 特定の \(x_0\) における 新しい1つの観測値 \(y_0\)。これは固定値ではなく、確率的に変動する確率変数です。
- 解釈の違い: 対象が固定値ではないため、解釈は少し直接的になりますが、根幹は同じです。
- 95%信頼度の意味(経験5年の場合): 「もし、何度も『①50日分のデータを取って予測区間を計算し、②その後、新たに経験5年のチームで1日営業してみる』というプロセスを繰り返せば、そのうち約95%の試行において、②で観測された実際の売上が、①で計算した予測区間の範囲内に収まるだろう。」 これは「95%の確率で未来を当てられる予測手法」と解釈できます。
ワーキング-ホテリング信頼帯
- 対象: 母回帰直線 \(Y = \alpha X + \beta\) そのもの。
- 95%信頼度の意味: 「もし、何度も50日間のデータを収集し直し、その都度、ワーキング-ホテリング信頼帯を計算すれば、その100個の帯のうち約95個は、“真の回帰直線”を、その全体にわたって、まるごとすっぽりと内部に含んでいるだろう。」 これは、特定の点だけでなく、直線全体を同時にカバーするという、非常に強い意味での信頼性を表しています。
以上です。