RStan を利用して 状態空間モデル(ローカルレベルモデル、パラメーター未知、季節性データ) を試みます。
1. ストーリーとシナリオ設定
シミュレーションの前提となるストーリーを設定します。
シナリオ:とある地方観光地の月間観光客数の変動
- 対象データ: ある地方の魅力的な観光地における、過去5年間(60か月)の月間観光客数(単位:千人)のデータ。
- データの特徴:
- 季節性: この観光地は、気候や連休の影響を強く受けます。具体的には、夏休みシーズンの7月・8月と、紅葉が美しい10月・11月に観光客が大幅に増加します。逆に、冬の1月・2月は寒さで客足が遠のきます。このパターンは毎年繰り返されるため、周期12か月の「季節性」として捉えることができます。
- 水準(ローカルレベル)の変動: 観光地の基本的な人気度(水準)は一定ではありません。例えば、以下のような予測不能なイベントによって、月ごとにランダムに変動します。
- ポジティブな変動: 人気テレビ番組で紹介された、SNSで「インスタ映えスポット」として話題になった、近隣で大規模なフェスティバルが開催された、など。
- ネガティブな変動: 長雨や台風、豪雪などの悪天候が続いた、周辺地域でネガティブなニュースがあった、など。
- システムノイズ: 上記の「水準の変動」は、モデルにおけるシステムノイズ
(sigma_w)に対応します。テレビ放映やSNSでのバズりは突発的かつその影響度も様々であるため、システムノイズは決して0に近くならず、ある程度の大きさを持つと想定されます。これは、観光地の潜在的な人気度が常にランダムウォークしていることを意味します。 - 観測ノイズ: 実際に記録される観光客数は、日々の細かな天候の変化や集計時のわずかな誤差など、上記の「水準」と「季節性」だけでは説明しきれないランダムなばらつきを含みます。これが観測ノイズ
(sigma_v)となります。
- シミュレーションの目的: この架空の観光客数データを用いて、観測データから「真の人気度の推移(水準)」、「毎年繰り返される季節変動」、そして「システムノイズと観測ノイズの大きさ」をシミュレーションで推定します。
2. Rによるサンプルデータの生成
まず、上記のシナリオに沿った時系列データをRで生成します。
seed <- 20250628
# シミュレーションの基本設定
set.seed(seed)
T <- 60 # データ期間 (5年 * 12か月)
S <- 12 # 季節周期 (12か月)
# ---- 真のパラメータ設定 ----
# 観測ノイズの標準偏差
sigma_v_true <- 2.0
# システムノイズの標準偏差
sigma_w_true <- 0.8
# ---- 真の状態の生成 ----
# 1. 真の水準(alpha)を生成 (ランダムウォーク)
alpha_true <- numeric(T)
alpha_true[1] <- 15 # 初期水準 (15千人)
for (t in 2:T) {
alpha_true[t] <- alpha_true[t - 1] + rnorm(1, mean = 0, sd = sigma_w_true)
}
# 2. 真の季節効果(gamma)を生成
# 合計が0になるように設定
gamma_s_true <- c(-7.9, -8.9, -2.8, 0.2, 2.2, 1.2, 7.2, 6.1, 0.2, 3.2, 4.1, -4.8)
gamma_true <- rep(gamma_s_true, times = T / S)
sum(gamma_s_true)[1] -5.551115e-16# ---- 観測データの生成 ----
y <- numeric(T)
for (t in 1:T) {
y[t] <- alpha_true[t] + gamma_true[t] + rnorm(1, mean = 0, sd = sigma_v_true)
}
# ---- 生成したデータの可視化 ----
true_data <- data.frame(
time = 1:T,
y = y,
alpha_true = alpha_true,
gamma_true = gamma_true
)
library(ggplot2)
ggplot(true_data, aes(x = time)) +
geom_line(aes(y = y, color = "観測値(y)"), linewidth = 1) +
geom_line(aes(y = alpha_true, color = "真の水準(alpha)"), linetype = "dashed", linewidth = 1) +
geom_line(aes(y = alpha_true + gamma_true, color = "真の水準+季節性"), linewidth = 1) +
labs(
title = "生成されたサンプルデータ",
subtitle = "観光地の月間観光客数(架空)",
x = "時間 (月)",
y = "観光客数 (千人)",
color = "データ系列"
) +
theme_bw()3. Stanコードの作成
次に、季節性ローカルレベルモデルをStanで記述します。なお、コードにはドメイン知識を盛り込みます。
- システムノイズ (
sigma_w): パラメータブロックでlower=0.1,upper=5.0の制約をかけます。- 下限
0.1: シナリオ上「全く変動がない」とは考えにくいため、ごく小さな正の値を設定します。 - 上限
5.0: 月次の水準が5千人以上もランダムに変動することは、よほどの異常事態を除き考えにくいというドメイン知識を反映させます。
- 下限
- 事前分布:
-
alpha[1](初期水準): 最初の観測値y[1]を中心とした、少し広めの分布を設定します。 -
sigma_w,sigma_v: ノイズのスケールとして、弱情報事前分布(正規分布)を設定します。
-
model_code <- "
data {
int<lower=1> T; // データ期間
int<lower=1> S; // 季節周期
vector[T] y; // 観測データ
}
parameters {
vector[T] alpha; // 水準(トレンド)
vector[S-1] gamma_ini; // 最初のS-1(=11)期間の季節効果
// 観測ノイズの標準偏差
real<lower=0> sigma_v;
// システムノイズの標準偏差
// ドメイン知識から下限(0.1)と上限(5.0)を設定
real<lower=0.1, upper=5.0> sigma_w;
}
transformed parameters {
vector[T] gamma; // 全期間の季節効果
// 確定的季節モデル(季節パターンは時間不変)の実装
// 最初のS-1個をパラメータから設定
gamma[1:(S-1)] = gamma_ini;
// S番目の季節効果は、合計が0になるように決定
gamma[S] = -sum(gamma_ini);
// S+1以降は周期的に同じ値を適用
for (t in (S+1):T) {
gamma[t] = gamma[t-S];
}
}
model {
// --- 事前分布 ---
// ドメイン知識の活用
// 各ノイズの標準偏差の事前分布
// (parametersブロックの制約により、自動的に切断正規分布になる)
sigma_v ~ normal(0, 5); // 観測ノイズは比較的大きい可能性がある
sigma_w ~ normal(0, 2); // システムノイズはそこそこの変動と想定
// 季節効果の初期値の事前分布
gamma_ini ~ normal(0, 5);
// 状態の初期値の事前分布
// 最初の観測値y[1]から大きくは外れないだろう、というドメイン知識
alpha[1] ~ normal(y[1], 10);
// --- 状態方程式 ---
// 水準はランダムウォークに従う
for (t in 2:T) {
alpha[t] ~ normal(alpha[t-1], sigma_w);
}
// --- 観測方程式 ---
// 観測値yは「水準+季節性」の周りに正規分布でばらつく
// ベクトル化表記で高速化
y ~ normal(alpha + gamma, sigma_v);
}
generated quantities {
// 予測分布を生成(モデルの当てはまり確認用)
vector[T] y_pred;
for (t in 1:T) {
y_pred[t] = normal_rng(alpha[t] + gamma[t], sigma_v);
}
}
"4. RStanによるシミュレーション実行と結果の分析
最後に、RからStanを呼び出してMCMCシミュレーションを実行し、結果を可視化・分析します。
# RStanの読み込み
library(rstan)
stan_output <- "D:/stan_output"
# Stanの並列計算設定
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
sapply(X = c("rstan"), packageVersion)$rstan
[1] 2 32 7# Stanに渡すデータ
stan_data <- list(T = T, S = S, y = y)
# MCMCの実行
fit <- stan(
model_code = model_code,
data = stan_data,
seed = seed,
chains = 4,
iter = 8000,
warmup = 4000,
thin = 1
)
# stanfit オブジェクトの保存
setwd(stan_output)
saveRDS(object = fit, file = "stan_fit.rds")# stanfit オブジェクトの読み込み
setwd(stan_output)
fit <- readRDS("stan_fit.rds")
# ---- 結果の確認 ----
# 1. パラメータの推定結果の要約
# 真の値 sigma_v=2.0, sigma_w=0.8
print(fit,
pars = c("sigma_v", "sigma_w", "lp__"),
probs = c(0.025, 0.5, 0.975)
)
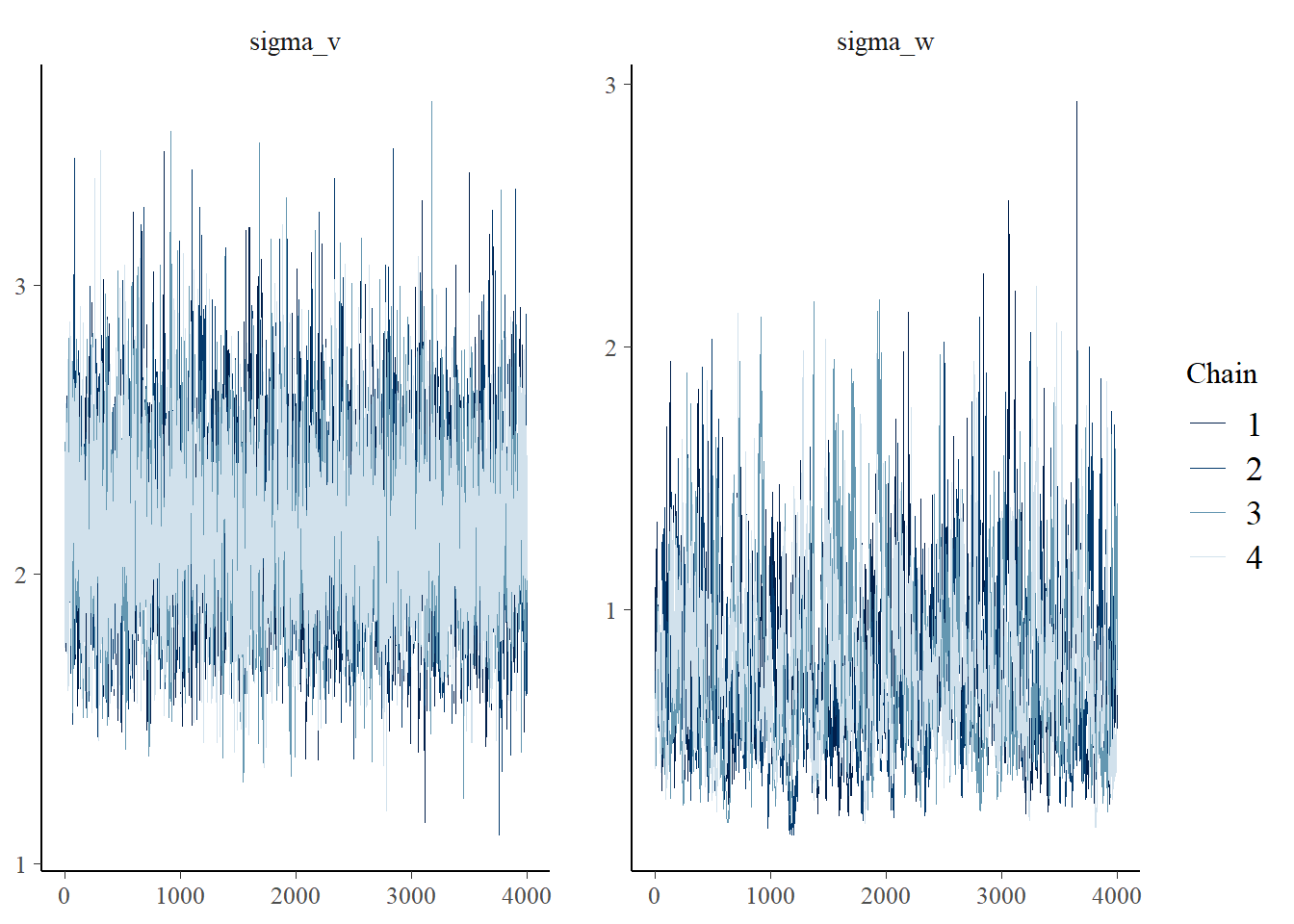
# トレースプロットを確認
bayesplot::mcmc_trace(fit, pars = c("sigma_v", "sigma_w"))Inference for Stan model: anon_model.
4 chains, each with iter=8000; warmup=4000; thin=1;
post-warmup draws per chain=4000, total post-warmup draws=16000.
mean se_mean sd 2.5% 50% 97.5% n_eff Rhat
sigma_v 2.14 0.00 0.28 1.63 2.13 2.76 3781 1.00
sigma_w 0.77 0.01 0.30 0.32 0.72 1.47 615 1.01
lp__ -89.27 0.86 19.66 -125.81 -89.80 -48.99 517 1.01
Samples were drawn using NUTS(diag_e) at Sat Jun 28 11:38:27 2025.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).stan実行の結果、以下の警告メッセージがでます。
警告メッセージ:
1: There were 4 chains where the estimated Bayesian Fraction of Missing Information was low. See

さらに、トレースプロットも きれいな結果 ではありませんが、sigma_vの真値が 2.0 に対して推定平均値は 2.14、sigma_w は真値が 0.80 に対して推定平均値は 0.77。いずれも95%信用区間に真値が含まれており、Rhat は 1.00 と 1.01 であるため、まぁいいだろうと自分を納得させて 先に進みます。
# 2. MCMCサンプルの抽出
mcmc_sample <- rstan::extract(fit)
# 3. 水準(alpha)の推定結果を可視化
alpha_est <- data.frame(
time = 1:T,
t(apply(mcmc_sample$alpha, 2, quantile, probs = c(0.025, 0.5, 0.975)))
)
colnames(alpha_est) <- c("time", "lower", "median", "upper")
ggplot(alpha_est, aes(x = time)) +
geom_ribbon(aes(ymin = lower, ymax = upper), fill = "skyblue", alpha = 0.5) +
geom_line(aes(y = median, color = "推定値(中央値)")) +
geom_line(data = true_data, aes(y = alpha_true, color = "真の値"), linetype = "dashed") +
labs(
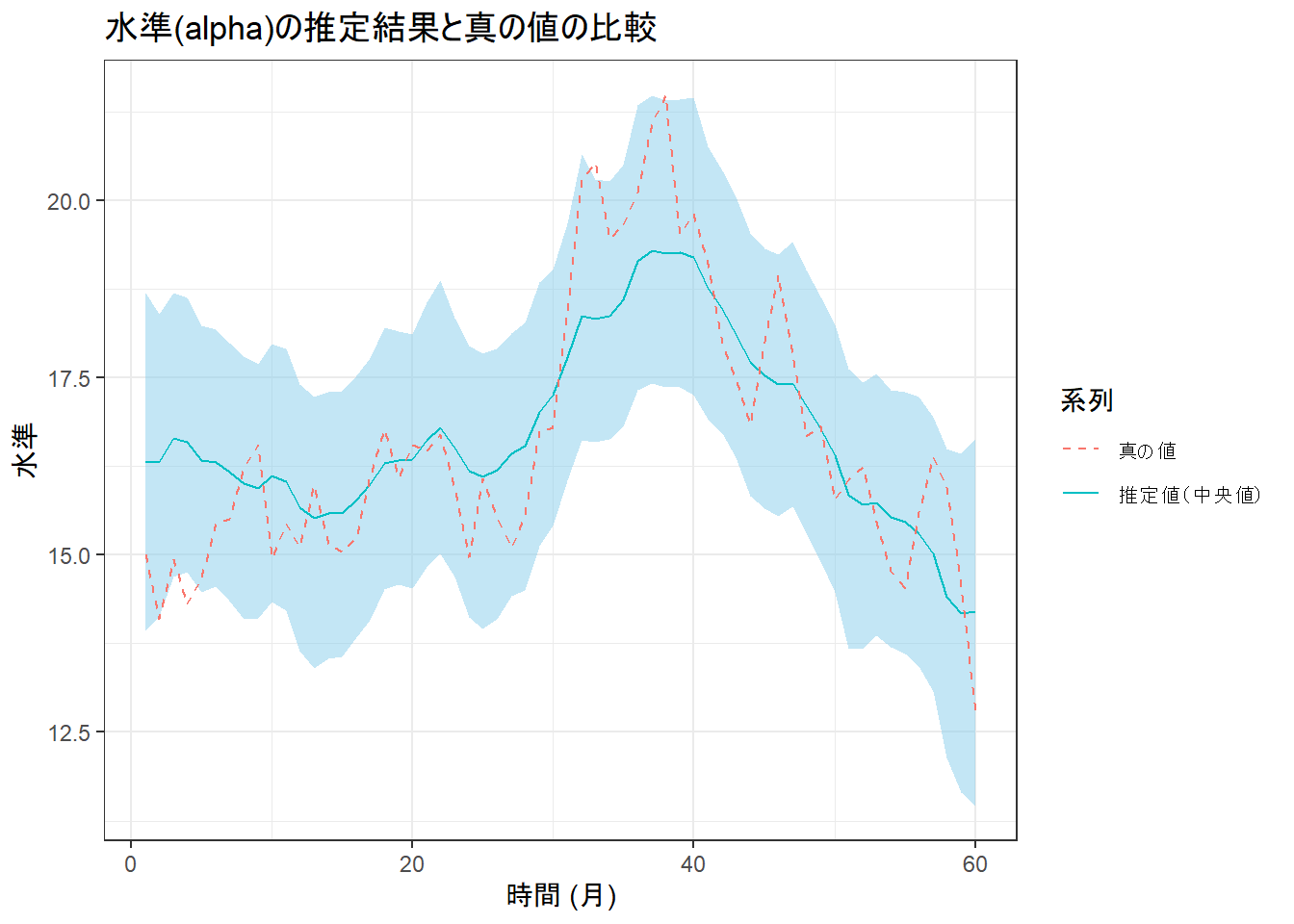
title = "水準(alpha)の推定結果と真の値の比較",
x = "時間 (月)", y = "水準", color = "系列"
) +
theme_bw()
# 4. 季節効果(gamma)の推定結果を可視化
gamma_est <- data.frame(
month = 1:S,
t(apply(mcmc_sample$gamma[, 1:S], 2, quantile, probs = c(0.025, 0.5, 0.975)))
)
colnames(gamma_est) <- c("month", "lower", "median", "upper")
ggplot(gamma_est, aes(x = month)) +
geom_ribbon(aes(ymin = lower, ymax = upper), fill = "lightgreen", alpha = 0.5) +
geom_line(aes(y = median, color = "推定値(中央値)")) +
geom_point(aes(y = median, color = "推定値(中央値)")) +
geom_line(data = data.frame(month = 1:S, y = gamma_s_true), aes(y = y, color = "真の値"), linetype = "dashed") +
scale_x_continuous(breaks = 1:12) +
labs(
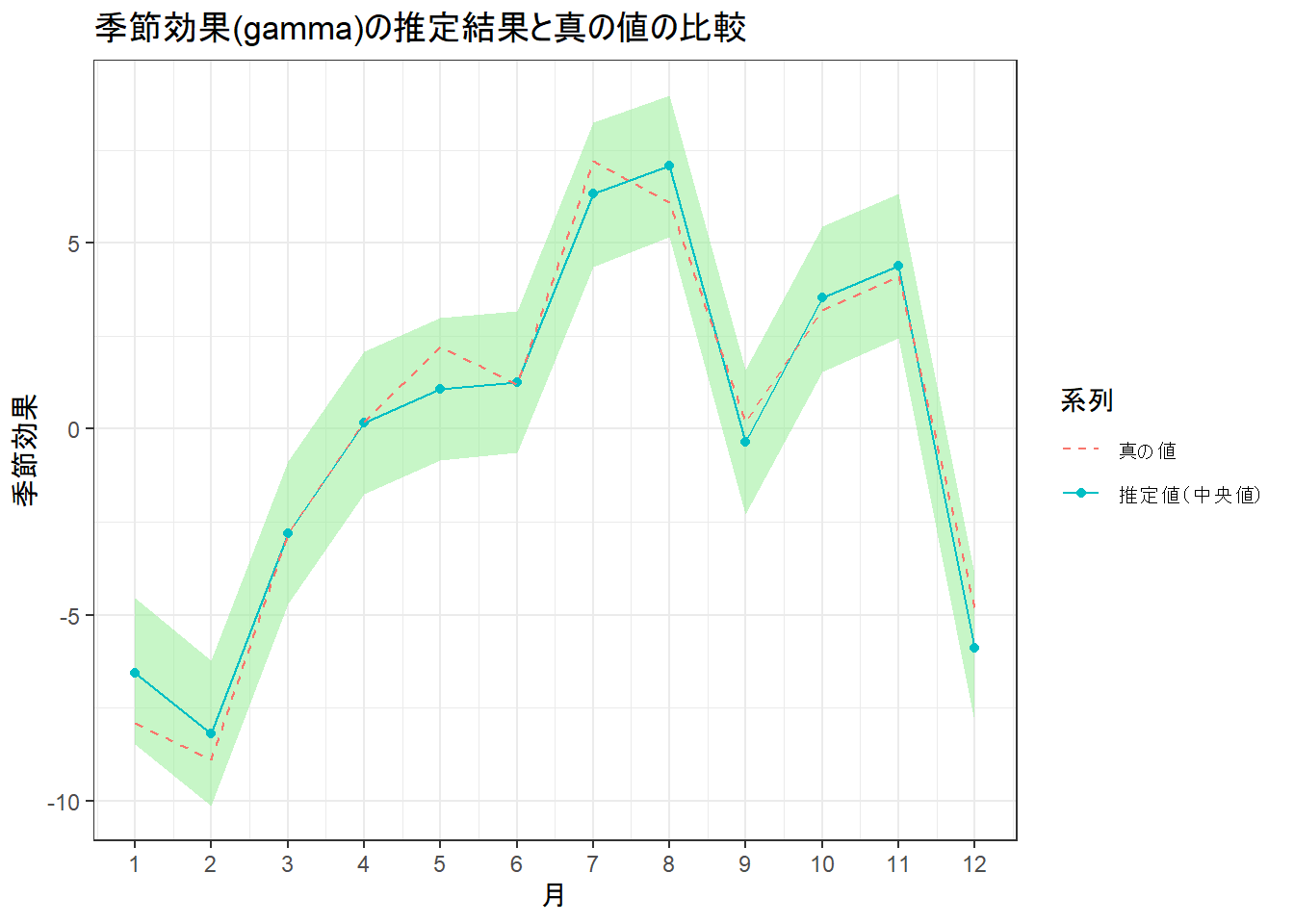
title = "季節効果(gamma)の推定結果と真の値の比較",
x = "月", y = "季節効果", color = "系列"
) +
theme_bw()
# 5. モデルの当てはまりを可視化
fit_summary <- summary(fit)$summary
y_median <- fit_summary[grep("alpha\\[", rownames(fit_summary)), "50%"] +
fit_summary[grep("gamma\\[", rownames(fit_summary)), "50%"]
fit_data <- data.frame(
time = 1:T,
y = y,
y_fit = y_median
)
ggplot(fit_data, aes(x = time)) +
geom_line(aes(y = y, color = "観測値"), linewidth = 1) +
geom_line(aes(y = y_fit, color = "モデルによる適合値"), linewidth = 1) +
labs(
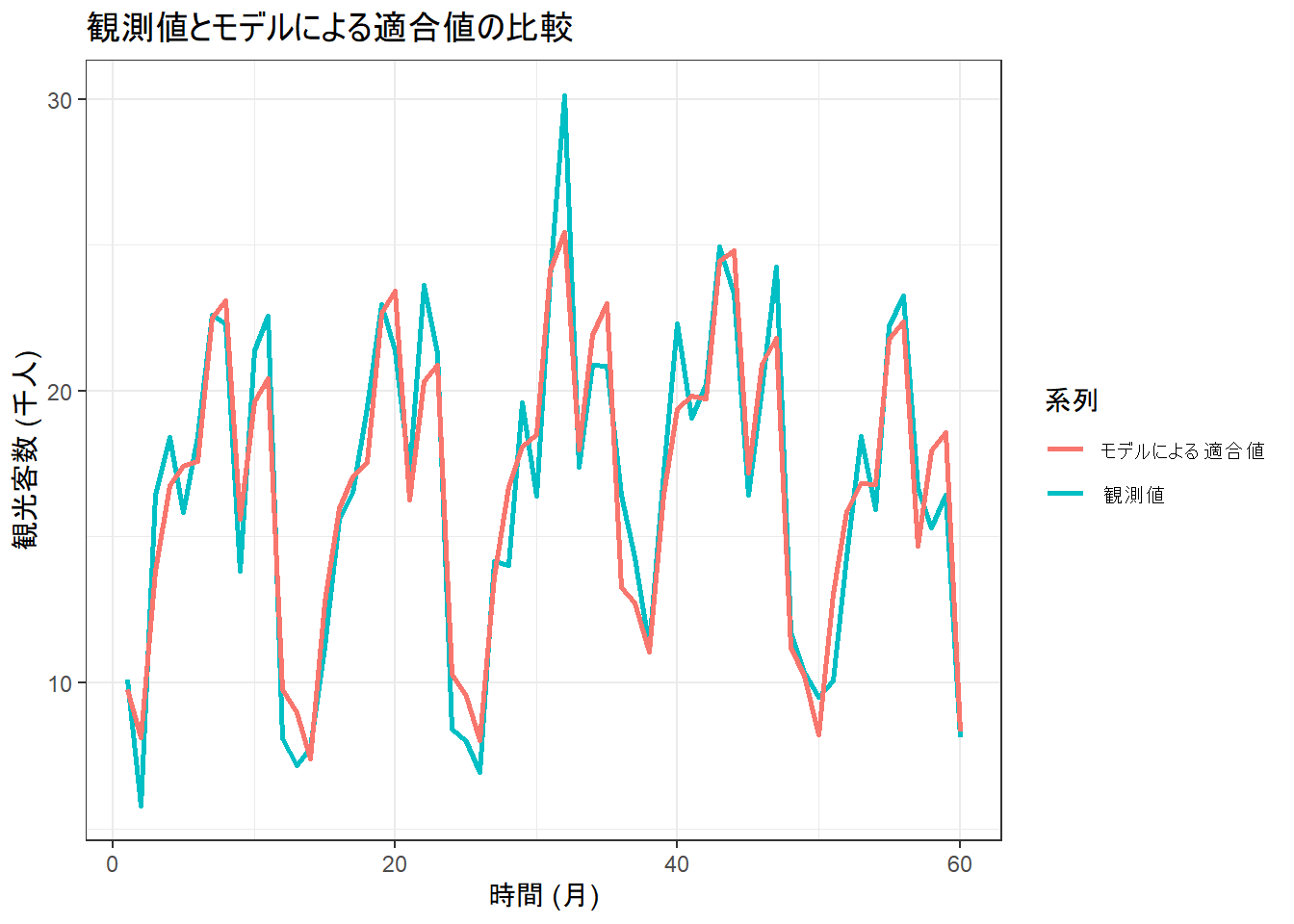
title = "観測値とモデルによる適合値の比較",
x = "時間 (月)", y = "観光客数 (千人)", color = "系列"
) +
theme_bw()結果の解釈
- 水準の推定: 「水準(alpha)の推定結果」(Figure 3)を見ますと、95%信用区間(水色の帯)が真の値を ほぼ カバーしています。
- 季節効果の推定: 「季節効果(gamma)の推定結果」(Figure 4)を見ますと、95%信用区間(緑色の帯)は真の12か月の季節パターンをカバーしています。
- モデルの当てはまり: Figure 5 は、観測値とモデルが予測する「水準+季節性」を比較したものです。モデルによる適合値が観測値の動きに ほぼ追従 できていることが確認できます。
以上です。