RStan を利用して 重回帰分析 を試みます。
1. シミュレーションのシナリオ:新規カフェの売上予測
ストーリー
あなたは、最近オープンした小さなカフェのオーナーです。開店から1か月(30営業日)が経ち、日々の売上データが少しずつ蓄積されてきました。
来月の食材仕入れやスタッフのシフトをより効率的に計画するため、日々の売上を予測するモデルを作りたいと考えています。
売上に影響しそうな要因として、以下の3つに目星をつけました。
- 目的変数 (Y): 1日の売上高 (
sales) - 説明変数
-
X1: その日の最高気温 (temperature) – 気温が高い日は、冷たいドリンクの売上が伸びそうです。 -
X2: SNS広告にかけた費用 (ad_cost) – 広告を出した日は、客足が増えるかもしれません。 -
X3: 近隣でのイベント開催の有無 (is_event) – 近くでイベントがあれば、普段よりお客さんが増えそうです(1: 開催あり, 0: 開催なし)。
-
課題と目的
- データが少ない: まだ30日分のデータしかなく、通常の統計手法では推定が不安定になる可能性があります。
- 経験の活用: あなたは以前別のカフェで働いていた経験から、「気温が1度上がると売上は1,000円くらい増える」、「イベントの日は20,000円くらい上乗せされる」といった肌感覚(事前知識)を持っています。
- 不確実性を知りたい: 単に「明日の売上は10万円です」という一点の予測だけではなく、「8万円から12万円の間に収まる確率が95%です」というように、予測の不確かさの幅も知りたいと考えています。これにより、仕入れの過不足リスクを管理できます。
これらの課題を解決するため、あなたはデータと自身の経験(事前知識)を統合でき、不確実性を確率分布として表現できるベイズ推定による重回帰分析を行うことにしました。
2. RとRStanによる重回帰分析の実装
それでは、上記のシナリオに沿ってシミュレーションを実行します。
Step 1: 環境準備とデータ生成
まず、必要なパッケージを読み込みます。
# RStanの読み込み
library(rstan)
stan_output <- "D:/stan_output"
# Stanの並列計算設定
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
# rstan のバージョン確認
cat("--- パッケージ rstan のバージョン確認 ---\n")
sapply(X = c("rstan"), packageVersion)--- パッケージ rstan のバージョン確認 ---
$rstan
[1] 2 32 7次に、シナリオに沿ったシミュレーションデータを生成します。
seed <- 20250629
set.seed(seed)
# 1. データ数(営業日数)
N <- 30
# 2. 真のパラメータを設定
true_intercept <- 50 # 基本売上(千円)
true_beta <- c(
1.0, # 気温が1度上がるごとの売上増(千円)
15.0, # 広告費1万円あたりの売上増(千円)
20.0 # イベント開催時の売上増(千円)
)
true_sigma <- 5.0 # 誤差の標準偏差(千円)
# 3. 説明変数を生成
# 気温 (15〜35℃)
temperature <- runif(N, 15, 35)
# SNS広告費 (0〜5万円)
ad_cost <- runif(N, 0, 5)
# イベントの有無 (開催確率20%)
is_event <- rbinom(N, 1, 0.2)
# 4. 目的変数(売上)を生成
# 行列形式で説明変数をまとめる
X <- cbind(temperature, ad_cost, is_event)
# 売上 = 切片 + X * β + 誤差
sales <- true_intercept + X %*% true_beta + rnorm(N, mean = 0, sd = true_sigma)
# データフレームにまとめる
sim_data <- data.frame(
sales = as.numeric(sales),
temperature,
ad_cost,
is_event
)
cat("--- 生成したデータの一部を確認 ---\n")
head(sim_data)--- 生成したデータの一部を確認 ---
sales temperature ad_cost is_event
1 118.37431 16.74056 3.6046917 0
2 145.13294 22.56467 4.7496321 0
3 77.90543 18.02118 0.8251549 0
4 115.89262 20.50424 2.9119301 0
5 142.39505 34.47013 3.7660024 0
6 109.73517 21.31454 2.7105428 0Step 2: Stanモデルの記述
次に、重回帰モデルをStanのコードで記述します。
model_code <- "
data {
int<lower=0> N; // データ数
int<lower=0> K; // 説明変数の数
matrix[N, K] X; // 説明変数の行列
vector[N] y; // 目的変数
}
parameters {
real intercept; // 切片
vector[K] beta; // 回帰係数
real<lower=0> sigma; // 誤差の標準偏差
}
model {
// --- 事前分布 ---
// 正規分布を仮定(弱情報事前分布)
intercept ~ normal(0, 100);
// スケールパラメータにはコーシー分布を仮定
sigma ~ cauchy(0, 5);
// 回帰係数(beta)に個別の事前分布を設定
// オーナーの「肌感覚」をモデルに組み込む
// beta[1]: 気温の効果。平均1.0(千円), 標準偏差0.5(千円)の正規分布を仮定
beta[1] ~ normal(1.0, 0.5);
// beta[2]: 広告費の効果。特に事前知識がないため、弱情報事前分布を適用
beta[2] ~ normal(0, 100);
// beta[3]: イベント開催の効果。平均20.0(千円), 標準偏差2.5(千円)の正規分布を仮定
beta[3] ~ normal(20.0, 2.5);
// --- 尤度(データが生成されるモデル) ---
// yは、平均が (切片 + X*beta) で、標準偏差がsigmaの正規分布に従う
y ~ normal(intercept + X * beta, sigma);
}
generated quantities {
// 予測分布を生成するための変数
vector[N] y_pred;
for (n in 1:N) {
y_pred[n] = normal_rng(intercept + X[n] * beta, sigma);
}
}
"Step 3: RからStanを実行(MCMCサンプリング)
Rに戻り、Stanに渡すデータを準備して、MCMCサンプリングを実行します。
# Stanに渡すためのデータをリスト形式で準備
stan_data <- list(
N = N,
K = ncol(X),
X = X,
y = as.vector(sales)
)
# StanモデルのコンパイルとMCMCの実行
fit <- stan(
model_code = model_code,
data = stan_data, # 入力データ
seed = seed, # 乱数シード
chains = 4, # MCMCのチェーン数
iter = 2000, # 1チェーンあたりの繰り返し数
warmup = 1000, # バーンイン期間
thin = 1 # 間引き数
)
# stanfit オブジェクトの保存
setwd(stan_output)
saveRDS(object = fit, file = "stan_fit.rds")Step 4: 結果の確認と解釈
MCMCサンプリングが完了したら、結果を確認します。
① 要約統計量
summary()関数で、各パラメータの事後分布に関する要約統計量(平均、標準偏差、信用区間など)を確認します。
# stanfit オブジェクトの読み込み
setwd(stan_output)
fit <- readRDS("stan_fit.rds")
summary(fit,
pars = c("intercept", "beta", "sigma"),
probs = c(0.025, 0.5, 0.975)
)$summary mean se_mean sd 2.5% 50% 97.5%
intercept 45.863751 0.118116701 5.1949373 35.526457 45.791465 55.838047
beta[1] 1.079772 0.003359879 0.1647286 0.765307 1.078060 1.416125
beta[2] 15.340120 0.013423003 0.6674183 14.058971 15.318481 16.684802
beta[3] 21.325944 0.036357269 2.0250225 17.361975 21.347005 25.215260
sigma 4.891527 0.013236023 0.6741103 3.749872 4.825901 6.390908
n_eff Rhat
intercept 1934.363 1.0005156
beta[1] 2403.758 1.0003069
beta[2] 2472.275 1.0000689
beta[3] 3102.253 1.0014669
sigma 2593.862 0.9997579結果の読み方:
-
mean: パラメータの事後分布の平均値(最も確からしい推定値)。 -
sd: 事後分布の標準偏差(推定値のばらつき)。 -
2.5%,97.5%: 95%信用区間。パラメータの真の値が95%の確率でこの範囲に含まれることを示します。 -
Rhat: 収束診断指標。1に近いほど、MCMCサンプリングがうまく収束したことを示します。
考察:
-
intercept(切片) の推定値の平均は45.9で、真の値50は95%信用区間[35.5, 55.8]に収まっています。 -
beta[1](気温) の推定値は1.1(真の値:1.0) -
beta[2](広告費) の推定値は15.3(真の値:15.0) -
beta[3](イベント) の推定値は21.3(真の値:20.0) -
sigma(誤差) の推定値は4.9(真の値:5.0)
すべてのパラメータの真の値が、推定された95%信用区間内に含まれており、警告メッセージ も出ていませんので、モデルがうまくデータを学習できていると判断できます。
② 事後分布の可視化
パラメータの事後分布をプロットすることで、推定値の不確かさを視覚的に理解できます。
# MCMCサンプルを抽出
mcmc_sample <- rstan::extract(fit)
# betaの事後分布をデータフレームに変換
beta_df <- as.data.frame(mcmc_sample$beta)
colnames(beta_df) <- c("temperature", "ad_cost", "is_event")
# ggplot2で可視化
library(dplyr)
library(ggplot2)
beta_df %>%
tidyr::pivot_longer(everything(), names_to = "parameter", values_to = "value") %>%
ggplot(aes(x = value, fill = parameter)) +
geom_density(alpha = 0.7) +
facet_wrap(~parameter, scales = "free") +
geom_vline(
data = . %>% group_by(parameter) %>% summarise(mean_val = mean(value)),
aes(xintercept = mean_val), linetype = "dashed", color = "red"
) +
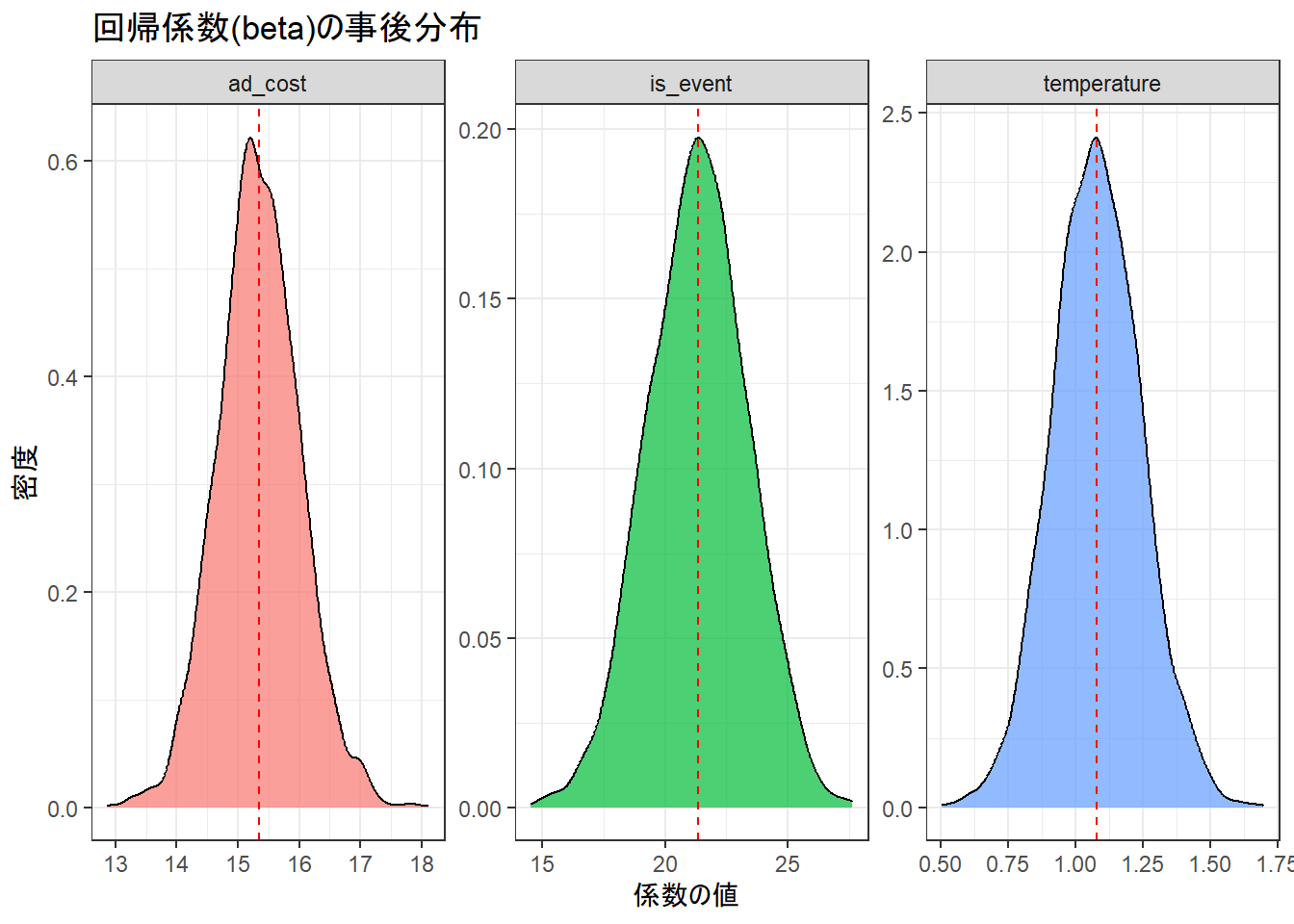
labs(title = "回帰係数(beta)の事後分布", x = "係数の値", y = "密度") +
theme_bw() +
theme(legend.position = "none")このプロットから、各係数がどのあたりにありそうか、そしてどの程度のばらつき(不確かさ)を持っているかを視覚的に理解できます。
3. 結論
今回の「新規カフェの売上予測」シナリオにおいて、
- 気温が1度あがると95%の確率で売上が 765円〜1416円増加 する。
- 広告費1万円あたり95%の確率で売上が 14059円~16685円増加 する。
- イベントが開催されると95%の確率で売上が 17362円~25215円増加 する。
ことが示唆されました。
以上です。