Rで ガウス=マルコフの定理 を確認します。
ガウス=マルコフの定理とは
ガウス=マルコフの定理は、、「ある一連の仮定が満たされるとき、最小二乗法(OLS)で得られる推定量は、考えられるすべての線形不偏推定量の中で最も分散が小さい(つまり、最も効率的である)」とする定理です。
この性質を持つ推定量を BLUE(Best Linear Unbiased Estimator)と呼びます。BLUEを分解すると、定理の主張がより明確になります。
- B (Best): 最良
- 「最も分散が小さい」ことを意味します。何度もサンプリングと推定を繰り返したとき、推定値のばらつきが最小になるということです。ばらつきが小さいほど、一度の推定で得られた値が真の値に近いと期待でき、信頼性が高まります。
- L (Linear): 線形
- 「線形推定量」であることを意味します。これは、回帰係数の推定量が、目的変数 \(y_i\) の線形結合(例: \(\hat{\beta} = \sum w_i y_i\))で計算できることを指します。OLS推定量はこの性質を満たします。
- U (Unbiased): 不偏
- 「不偏推定量」であることを意味します。これは、何度もサンプリングと推定を繰り返したとき、その推定値の期待値(平均)が、推定したい真のパラメータ値と一致することを指します。つまり、推定に「偏り(バイアス)」がないということです。
定理が成立するための仮定
ガウス=マルコフの定理が成立するためには、誤差項 \(\epsilon\) に関して以下の仮定が満たされる必要があります。
線形性 (Linearity in Parameters): モデルはパラメータ(\(\beta_0, \beta_1\)など)について線形である。 \(y = \beta_0 + \beta_1 x + \epsilon\)
誤差項の期待値はゼロ (Zero Conditional Mean): 任意の説明変数 \(x\) の値に対して、誤差項 \(\epsilon\) の期待値は0である。 \(E[\epsilon | x] = 0\) これは、誤差と説明変数が無関係であることを意味します(外生性の仮定)。
均一分散 (Homoscedasticity): 誤差項 \(\epsilon\) の分散は、説明変数 \(x\) の値によらず一定である。 \(Var(\epsilon | x) = \sigma^2\)
系列無相関 (No Serial Correlation): 異なる観測値における誤差項同士は、互いに相関しない。 \(Cov(\epsilon_i, \epsilon_j | x) = 0 \quad (i \neq j)\)
(重回帰の場合) 完全共線性がない (No Perfect Collinearity): 説明変数同士が完全な線形関係にない。
これらの仮定が満たされたとき、OLS推定量はBLUEとなります。なお、誤差項が正規分布に従うという仮定は、BLUEであるためには必要ありません。(正規性の仮定は、推定量の仮説検定や信頼区間の導出の際に必要となります。)
Rによるシミュレーション
それでは、この定理を体験的に理解するためのシミュレーションを行います。 ここでは、OLS推定量が、比較対象となる別の「線形不偏推定量」よりも実際に分散が小さくなる(=Bestである)ことを確認します。
シミュレーションの設計
- 真のモデル \(y = \beta_0 + \beta_1 x + \epsilon\) を設定します。
- 上記のガウス=マルコフの仮定を満たすデータを生成します。
- 生成したデータから、以下の2種類の方法で傾き \(\beta_1\) を推定します。
- 推定量A (OLS): 最小二乗法による推定量。これがBLUEであるはずです。
- 推定量B (代替案): 別の線形不偏推定量。ここでは例として「最初と最後の観測点だけを使って傾きを計算する推定量」を使います。この推定量も線形で不偏ですが、OLSのように全てのデータを使っていないため、効率性は低いはずです。
- このプロセスを 100000 回繰り返し、それぞれの推定量の分布を記録します。
- 最後に、2つの推定量の分布を比較し、両者とも不偏(分布の平均が真の値に近い)であるが、OLS推定量の分布の方がよりシャープ(分散が小さい)であることを確認します。
Rコード
seed <- 20250707
options(scipen = 999)
# 必要なパッケージをロード
library(ggplot2)
# ----- 1. シミュレーションの準備 -----
set.seed(seed) # 結果の再現性を確保するための乱数シード
n_sim <- 100000 # シミュレーションの繰り返し回数
n_obs <- 100 # 1回あたりのサンプルサイズ
# 真のパラメータを設定
beta0_true <- 5 # 真の切片
beta1_true <- 2 # 真の傾き
sigma_e <- 10 # 誤差項の標準偏差 (均一分散)
# 説明変数 x を生成 (シミュレーション中は固定)
x <- 1:n_obs
# 結果を保存するためのベクトルを初期化
beta1_ols <- numeric(n_sim) # OLSによる推定値を保存
beta1_alt <- numeric(n_sim) # 代替案による推定値を保存
# ----- 2. シミュレーションの実行 -----
for (i in 1:n_sim) {
# ガウス=マルコフの仮定を満たす誤差項を生成
# E[e]=0, Var(e)=sigma_e^2, 互いに無相関
epsilon <- rnorm(n = n_obs, mean = 0, sd = sigma_e)
# 観測データ y を生成
y <- beta0_true + beta1_true * x + epsilon
# 【推定量A: OLS (BLUE)】
# lm()関数で最小二乗法による回帰分析を実行
model_ols <- lm(y ~ x)
beta1_ols[i] <- coef(model_ols)[2] # 傾きの推定値を保存
# 【推定量B: 代替の線形不偏推定量】
# 最初と最後のデータ点のみを使って傾きを計算
# この推定量も線形(yの線形結合)かつ不偏(期待値がbeta1_trueになる)
beta1_alt[i] <- (y[n_obs] - y[1]) / (x[n_obs] - x[1])
}
# ----- 3. 結果の分析 -----
cat("シミュレーション結果の要約:\n")
cat("----------------------------------\n")
cat("真の傾き (β1):", beta1_true, "\n\n")
cat("【OLS推定量】\n")
cat(" 平均値:", mean(beta1_ols), " (不偏性の確認)\n")
cat(" 真の価(=2)からの乖離:", abs(beta1_true - mean(beta1_ols)), "\n")
cat(" 分散: ", var(beta1_ols), " (効率性の確認)\n\n")
cat("【代替推定量】\n")
cat(" 平均値:", mean(beta1_alt), " (不偏性の確認)\n")
cat(" 真の価(=2)からの乖離:", abs(beta1_true - mean(beta1_alt)), "\n")
cat(" 分散: ", var(beta1_alt), " (効率性の確認)\n")
cat("----------------------------------\n")
cat(sprintf(
"OLS推定量の分散は、代替推定量の分散の %.2f %% です。\n",
var(beta1_ols) / var(beta1_alt) * 100
))シミュレーション結果の要約:
----------------------------------
真の傾き (β1): 2
【OLS推定量】
平均値: 2.000012 (不偏性の確認)
真の価(=2)からの乖離: 0.00001192939
分散: 0.001207354 (効率性の確認)
【代替推定量】
平均値: 1.999942 (不偏性の確認)
真の価(=2)からの乖離: 0.00005800531
分散: 0.02044202 (効率性の確認)
----------------------------------
OLS推定量の分散は、代替推定量の分散の 5.91 % です。この数値結果から、以下の2点が確認できます。
- 不偏性 (Unbiased): OLS推定量と代替推定量の平均値は、両方とも真の値である
2に近くなっています。これは、どちらの推定量も不偏であることを示唆しています。 - 最小分散性 (Best): OLS推定量の分散 (
0.0012) は、代替推定量の分散 (0.0204) よりも小さいことがわかります。
# ----- 4. 結果の可視化 -----
# プロット用にデータを整形
results_df <- data.frame(
estimate = c(beta1_ols, beta1_alt),
estimator = factor(rep(c("OLS推定量 (BLUE)", "代替推定量"), each = n_sim))
)
# 密度プロットを作成
ggplot(results_df, aes(x = estimate, fill = estimator)) +
geom_density(alpha = 0.6) +
# 真の値を表す垂直線を追加
geom_vline(xintercept = beta1_true, color = "red", linetype = "dashed", linewidth = 1.2) +
# scale_fill_manualの凡例キーをデータフレームのfactorレベル名と合わせる
scale_fill_manual(values = c("OLS推定量 (BLUE)" = "#0072B2", "代替推定量" = "#E69F00")) +
labs(
title = "ガウス=マルコフの定理のシミュレーション",
subtitle = paste("OLS推定量と他の線形不偏推定量の分布の比較 (N =", n_sim, ")"),
x = "傾き β1 の推定値",
y = "密度",
fill = "推定量"
) +
# 真の値のテキストを追加
annotate("text",
x = beta1_true * 1.02, y = 1, hjust = 0,
label = paste("真の値 β₁ =", beta1_true), color = "red", size = 4
) +
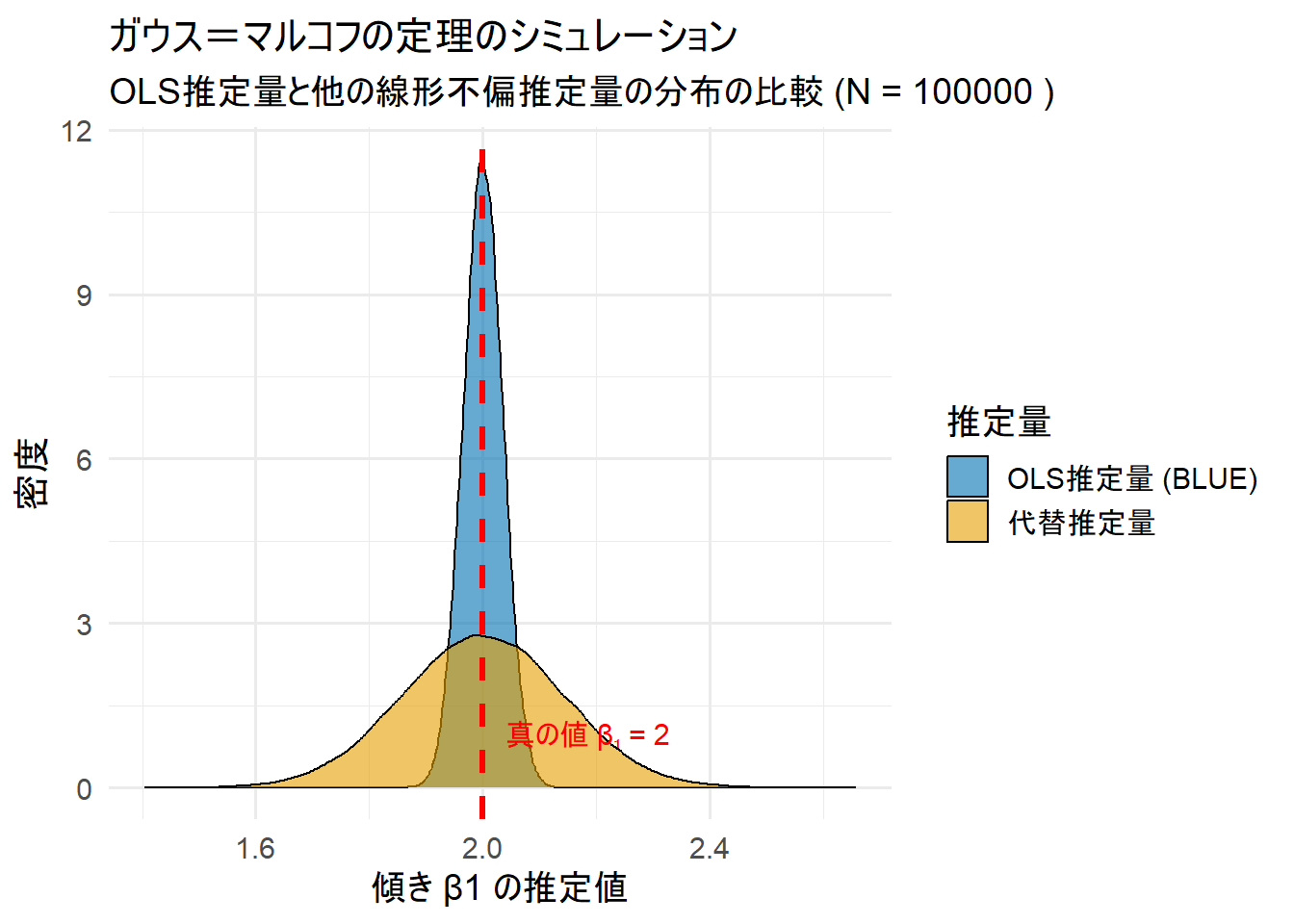
theme_minimal(base_size = 14)Figure 1 は、100000 回分の推定値の分布を密度曲線で表したものです。
- 赤い破線は、推定したい真の傾き
β₁ = 2の位置を示しています。 - 2つの分布(青色のOLSとオレンジ色の代替推定量)は、どちらもこの赤い破線をほぼ中心にしており、不偏性を視覚的に確認できます。
- 青色のOLS推定量の分布は、オレンジ色の代替推定量の分布に比べてシャープで、中心に密集しています。これはOLS推定量の分散が小さいこと、つまり推定値のばらつきが少ないことを意味します。
以上です。