Rで サンプルサイズ設計:効果量・検定力・第一種過誤・第二種過誤 を確認します。
1. 各概念の説明
統計的仮説検定を行う際、私たちは限られたサンプルデータから母集団全体に関する結論を導き出そうとします。しかし、その判断には常に「誤り」を犯す可能性が伴います。これらの概念は、その誤りのリスクを管理し、意味のある結論を導くために不可欠です。
第一種過誤 (Type I Error, α)
- 定義: 「帰無仮説(H₀: 差がない、効果がない)が真であるにもかかわらず、それを誤って棄却してしまう」誤りです。
- 別名: 「偽陽性 (False Positive)」、「あわてものの誤り」。
- 確率: α (アルファ)で表され、有意水準とも呼ばれます。研究者が事前に設定する値で、通常は 0.05 (5%) や 0.01 (1%) が用いられます。
- 例: 「実際には効果がない新薬を、効果があると結論づけてしまう」ケースです。
第二種過誤 (Type II Error, β)
- 定義: 「対立仮説(H₁: 差がある、効果がある)が真であるにもかかわらず、帰無仮説を棄却できない(つまり、対立仮説を採択できない)」誤りです。
- 別名: 「偽陰性 (False Negative)」、「ぼんやりものの誤り」。
- 確率: β (ベータ)で表されます。
- 例: 「実際には効果がある新薬を、効果がないと見過ごしてしまう」ケースです。
検定力 (Statistical Power, 1-β)
- 定義: 「対立仮説が真であるときに、正しく帰無仮説を棄却できる」確率です。
- 計算: 1 – β で計算されます。
- 意味: 「本当に存在する効果を、正しく検出できる能力」を示します。研究計画の段階では、この検定力を十分に高く(慣例的に 80% 以上)設定することが目標となります。
- 例: 「効果がある新薬を、正しく『効果あり』と結論づける確率」です。
効果量 (Effect Size)
- 定義: 観測された現象の「大きさ」や「強さ」を示す標準化された指標です。例えば、2群の平均値の差が、ばらつき(標準偏差)に対してどの程度大きいかを示します。
- 重要性: p値はサンプルサイズに大きく依存しますが、効果量はサンプルサイズの影響を受けにくいため、結果の「実質的な重要性」を評価するのに役立ちます。
- 例: Cohen’s d、相関係数 r など。効果量が大きいほど、小さなサンプルサイズでもその効果を検出しやすくなります。
関係性のまとめ
これらの4つの要素は、以下の関係にあります。
- αとβのトレードオフ: 他の条件が同じなら、第一種過誤(α)を犯すリスクを低く設定する(有意水準を厳しくする)と、第二種過誤(β)を犯すリスクが高まり、検定力(1-β)は低下します。
- 検定力に影響する3要素:
- サンプルサイズ (N): 大きいほど、検定力は高くなります。
- 効果量 (Effect Size): 大きいほど、検定力は高くなります。
- 有意水準 (α): 大きい(緩い)ほど、検定力は高くなります。
研究を計画する際、研究者は許容できるα(例: 0.05)、検出したい効果量(先行研究などから想定)、達成したい検定力(例: 0.8)を設定し、それらを満たすために必要なサンプルサイズを計算します。これを検定力分析 (Power Analysis) と呼びます。
2. R言語によるシミュレーション
ここでは、2つの独立したグループ(例:対照群と実験群)の平均値の差をt検定で比較するシナリオを考えます。
準備
必要なライブラリを読み込みます。
library(tidyverse)
library(pwr)
seed <- 202507062.1. 概念の可視化
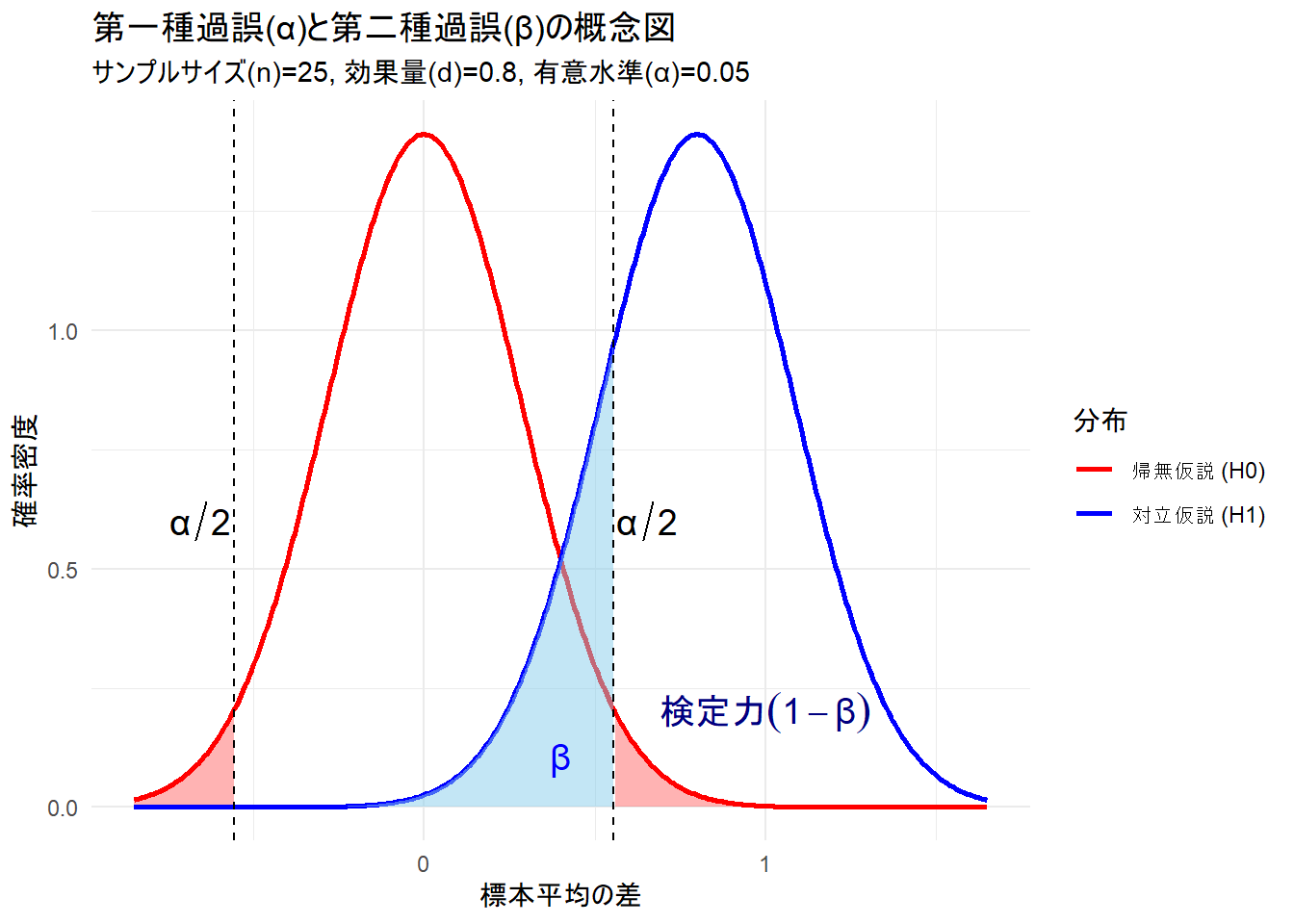
まず、帰無仮説(差がない)と対立仮説(差がある)がそれぞれ真である場合の標本平均の分布を可視化し、αとβがどこに位置するのかを確認しましょう。
# パラメータ設定
mu_h0 <- 0 # 帰無仮説の母平均の差
mu_h1 <- 0.8 # 対立仮説の母平均の差(効果量大)
sd <- 1 # 母標準偏差(両群共通と仮定)
n <- 25 # 各群のサンプルサイズ
alpha <- 0.05 # 有意水準
# 標準誤差の計算
se <- sd * sqrt(1 / n + 1 / n)
# 棄却域の境界値(臨界値)を計算
critical_value <- qnorm(1 - alpha / 2, mean = mu_h0, sd = se)
# 分布のデータを作成
dist_df <- tibble(
x = seq(-3 * se, mu_h1 + 3 * se, length.out = 400),
h0_density = dnorm(x, mean = mu_h0, sd = se),
h1_density = dnorm(x, mean = mu_h1, sd = se)
)
# プロット
ggplot(dist_df, aes(x = x)) +
# 帰無仮説の分布
geom_line(aes(y = h0_density, color = "帰無仮説 (H0)"), linewidth = 1) +
geom_area(
data = . %>% filter(x > critical_value),
aes(y = h0_density), fill = "red", alpha = 0.3
) +
geom_area(
data = . %>% filter(x < -critical_value),
aes(y = h0_density), fill = "red", alpha = 0.3
) +
# 対立仮説の分布
geom_line(aes(y = h1_density, color = "対立仮説 (H1)"), linewidth = 1) +
geom_area(
data = . %>% filter(x < critical_value & x > -critical_value),
aes(y = h1_density), fill = "skyblue", alpha = 0.5
) +
# 凡例と注釈
geom_vline(xintercept = c(critical_value, -critical_value), linetype = "dashed", color = "black") +
annotate("text", x = critical_value + 0.1, y = 0.6, label = "α/2", parse = TRUE, size = 5) +
annotate("text", x = -critical_value - 0.1, y = 0.6, label = "α/2", parse = TRUE, size = 5) +
annotate("text", x = 0.4, y = 0.1, label = "β", parse = TRUE, size = 5, color = "blue") +
annotate("text", x = 1.0, y = 0.2, label = "検定力 (1-β)", parse = TRUE, size = 5, color = "navy") +
scale_color_manual(name = "分布", values = c("帰無仮説 (H0)" = "red", "対立仮説 (H1)" = "blue")) +
labs(
title = "第一種過誤(α)と第二種過誤(β)の概念図",
subtitle = paste0("サンプルサイズ(n)=", n, ", 効果量(d)=", mu_h1, ", 有意水準(α)=", alpha),
x = "標本平均の差",
y = "確率密度"
) +
theme_minimal()- 赤い領域 (α): 帰無仮説が真(差がない)なのに、偶然、大きな差が観測され、誤って「差がある」と判断してしまう確率(第一種過誤)。
- 青い領域 (β): 対立仮説が真(本当に差がある)なのに、その差を検出できず、「差がない」という判断を覆せない確率(第二種過誤)。
- 青い分布のβ以外の領域: 本当に差があるときに、正しく「差がある」と判断できる確率(検定力)。
2.2. 第一種過誤 (α) のシミュレーション
帰無仮説が真(2つの母集団に全く差がない)の状況で、何度もサンプリングと検定を繰り返すと、設定した有意水準(α)の割合で誤って有意な結果が出てしまうことを確認します。
# シミュレーションのパラメータ設定
set.seed(seed) # 結果を再現可能にするための乱数シード
n_sim <- 5000 # シミュレーション回数
n_alpha <- 50 # サンプルサイズ
alpha_level <- 0.05 # 有意水準
# 帰無仮説が真の状況 (母平均の差が0)
mu1 <- 100
mu2 <- 100 # 差がない
sd <- 15
# p値を格納するベクトル
p_values_h0 <- numeric(n_sim)
for (i in 1:n_sim) {
# 2つの母集団からサンプリング
sample1 <- rnorm(n_alpha, mean = mu1, sd = sd)
sample2 <- rnorm(n_alpha, mean = mu2, sd = sd)
# t検定を実行
test_result <- t.test(sample1, sample2)
# p値を取得
p_values_h0[i] <- test_result$p.value
}
# 第一種過誤のシミュレーション結果
simulated_alpha <- sum(p_values_h0 < alpha_level) / n_sim
cat("--- 第一種過誤(α)のシミュレーション ---")
cat("\n設定した有意水準 (α):", alpha_level)
cat("\nシミュレーションで観測された第一種過誤の割合:", simulated_alpha)--- 第一種過誤(α)のシミュレーション ---
設定した有意水準 (α): 0.05
シミュレーションで観測された第一種過誤の割合: 0.0492シミュレーション結果は、設定した有意水準 0.05 に近い値となりました。これは、差がない場合でも5%の確率で「有意な差あり」という誤った結論を出してしまうことを意味します。
2.3. 検定力 (1-β) と第二種過誤 (β) のシミュレーション
次に対立仮説が真(2つの母集団に実際に差がある)の状況で、どのくらいの確率でその差を検出できるか(検定力)を見てみましょう。
# シミュレーションのパラメータ設定
set.seed(seed)
n_power <- 50 # サンプルサイズ(αのシミュレーションと同じ)
effect_size_d <- 0.5 # Cohen's d で効果量を設定(中程度の効果)
# 対立仮説が真の状況 (母平均に差がある)
mu1 <- 100
sd <- 15
mu2 <- mu1 + effect_size_d * sd # mu2 = 100 + 0.5 * 15 = 107.5
# p値を格納するベクトル
p_values_h1 <- numeric(n_sim)
for (i in 1:n_sim) {
# 2つの母集団からサンプリング
sample1 <- rnorm(n_power, mean = mu1, sd = sd)
sample2 <- rnorm(n_power, mean = mu2, sd = sd)
# t検定を実行
test_result <- t.test(sample1, sample2)
# p値を取得
p_values_h1[i] <- test_result$p.value
}
# 検定力と第二種過誤のシミュレーション結果
simulated_power <- sum(p_values_h1 < alpha_level) / n_sim
simulated_beta <- 1 - simulated_power
cat("--- 検定力(1-β)と第二種過誤(β)のシミュレーション ---")
cat("\nサンプルサイズ:", n_power)
cat("\n設定した効果量 (Cohen's d):", effect_size_d)
cat("\nシミュレーションで観測された検定力 (1-β):", simulated_power)
cat("\nシミュレーションで観測された第二種過誤の確率 (β):", simulated_beta)--- 検定力(1-β)と第二種過誤(β)のシミュレーション ---
サンプルサイズ: 50
設定した効果量 (Cohen's d): 0.5
シミュレーションで観測された検定力 (1-β): 0.6932
シミュレーションで観測された第二種過誤の確率 (β): 0.3068サンプルサイズ50、効果量0.5のとき、検定力は約70% (0.6932) となりました。これは、本当に差がある場合に、それを70%の確率で正しく検出できることを意味します。逆に、約30% (0.3068) の確率で、存在するはずの差を見逃してしまう(第二種過誤)ことになります。
2.4. サンプルサイズ、効果量、検定力の関係性のシミュレーション
最後に、サンプルサイズと効果量が検定力にどのように影響するかをシミュレーションし、可視化します。
# シミュレーションを実行する関数を定義
run_power_simulation <- function(n, effect_size, n_sim = 500, alpha = 0.05) {
mu1 <- 100
sd <- 15
mu2 <- mu1 + effect_size * sd
p_values <- replicate(n_sim, {
sample1 <- rnorm(n, mean = mu1, sd = sd)
sample2 <- rnorm(n, mean = mu2, sd = sd)
t.test(sample1, sample2)$p.value
})
power <- sum(p_values < alpha) / n_sim
return(power)
}
# シミュレーションのパラメータを設定
sample_sizes <- seq(10, 200, by = 10)
effect_sizes <- c(0.2, 0.5, 0.8) # 小、中、大の効果量
# expand.gridで全ての組み合わせを作成
sim_params <- expand.grid(
n = sample_sizes,
d = effect_sizes
)
# シミュレーションを実行
# mapplyを使って各パラメータの組み合わせでシミュレーションを実行
set.seed(seed)
sim_results <- mapply(
run_power_simulation,
n = sim_params$n,
effect_size = sim_params$d
)
# 結果をデータフレームに格納
results_df <- sim_params %>%
mutate(
power = sim_results,
effect_size_label = factor(paste0("d = ", d))
)
# 結果をプロット
ggplot(results_df, aes(x = n, y = power, color = effect_size_label)) +
geom_line(linewidth = 1.0) +
geom_point(size = 2.5) +
geom_hline(yintercept = 0.8, linetype = "dashed", color = "red") +
annotate("text", x = 150, y = 0.85, label = "目標検定力 (80%)", color = "red") +
scale_y_continuous(labels = scales::percent, limits = c(0, 1)) +
labs(
title = "サンプルサイズと効果量が検定力に与える影響",
x = "各群のサンプルサイズ (n)",
y = "検定力 (Power)",
color = "効果量 (Cohen's d)"
) +
theme_bw(base_size = 14)
# 必要サンプルサイズの計算
# ------------------------------------------------------------------
# パラメータ設定
# ------------------------------------------------------------------
target_power <- 0.8 # 目標とする検定力 (80%)
sig_level <- 0.05 # 有意水準 (5%)
# ------------------------------------------------------------------
# 1. 効果量 大 (d = 0.8) の場合
# ------------------------------------------------------------------
power_calc_large <- pwr.t.test(
d = 0.8,
power = target_power,
sig.level = sig_level,
type = "two.sample", # 2つの独立したサンプルの検定
alternative = "two.sided" # 両側検定
)
# ------------------------------------------------------------------
# 2. 効果量 中 (d = 0.5) の場合
# ------------------------------------------------------------------
power_calc_medium <- pwr.t.test(
d = 0.5,
power = target_power,
sig.level = sig_level,
type = "two.sample",
alternative = "two.sided"
)
# ------------------------------------------------------------------
# 3. 効果量 小 (d = 0.2) の場合
# ------------------------------------------------------------------
power_calc_small <- pwr.t.test(
d = 0.2,
power = target_power,
sig.level = sig_level,
type = "two.sample",
alternative = "two.sided"
)
# ------------------------------------------------------------------
# 結果の表示
# ------------------------------------------------------------------
cat("--- 有意水準5%、目標検定力80%を達成するために必要な各群のサンプルサイズ ---\n\n")
# 効果量 大 (d = 0.8)
cat("■ 効果量 大 (d = 0.8) の場合:\n")
print(power_calc_large)
# サンプルサイズは整数であるため、計算結果を切り上げる
cat("=> 必要なサンプルサイズ (各群):", ceiling(power_calc_large$n), "人\n\n")
# 効果量 中 (d = 0.5)
cat("■ 効果量 中 (d = 0.5) の場合:\n")
print(power_calc_medium)
cat("=> 必要なサンプルサイズ (各群):", ceiling(power_calc_medium$n), "人\n\n")
# 効果量 小 (d = 0.2)
cat("■ 効果量 小 (d = 0.2) の場合:\n")
print(power_calc_small)
cat("=> 必要なサンプルサイズ (各群):", ceiling(power_calc_small$n), "人\n")--- 有意水準5%、目標検定力80%を達成するために必要な各群のサンプルサイズ ---
■ 効果量 大 (d = 0.8) の場合:
Two-sample t test power calculation
n = 25.52458
d = 0.8
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
=> 必要なサンプルサイズ (各群): 26 人
■ 効果量 中 (d = 0.5) の場合:
Two-sample t test power calculation
n = 63.76561
d = 0.5
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
=> 必要なサンプルサイズ (各群): 64 人
■ 効果量 小 (d = 0.2) の場合:
Two-sample t test power calculation
n = 393.4057
d = 0.2
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
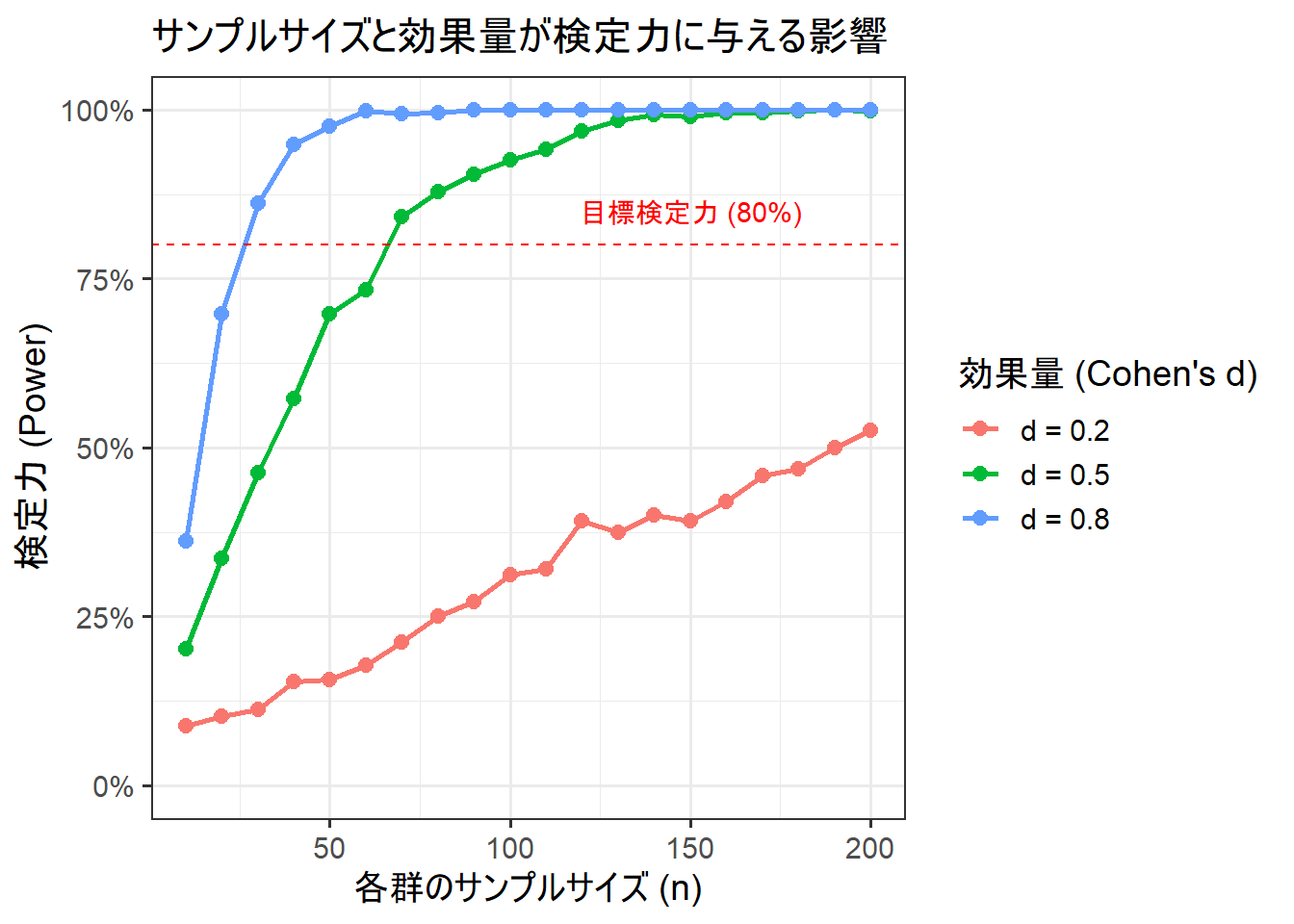
=> 必要なサンプルサイズ (各群): 394 人Figure 2 から以下のことが分かります。
- サンプルサイズが大きいほど、検定力は高まる: どの効果量でも、グラフは右肩上がりになっています。
- 効果量が大きいほど、検定力は高まる: 同じサンプルサイズ(例えば n=50)で比較すると、効果量
d=0.8の線が最も高く、d=0.2の線が最も低くなっています。 - 目標達成に必要なサンプルサイズ: 赤い点線(有意水準5%、目標検定力80%)を達成するために必要なサンプルサイズは、効果量によって大きく異なります。
- 効果量 大 (d=0.8): n=26 で達成
- 効果量 中 (d=0.5): n=64 で達成
- 効果量 小 (d=0.2): n=394 が必要(このグラフの範囲外)
このように、研究計画の段階で、想定される効果量に基づいて十分なサンプルサイズを確保することが、意味のある結果を得るために重要であることがシミュレーションを通して理解できます。
以上です。