Rで サンプルサイズ設計:t検定(2群、対応あり) を確認します。
1. シミュレーションのシナリオ
シナリオ:新しい記憶術トレーニングの効果測定
ある教育心理学の研究者が、新しく開発した記憶術トレーニングが、大学生の短期記憶能力を向上させるか検証したいと考えています。
- 研究の目的: 新しい記憶術トレーニングは、受講前と比較して、短期記憶テストのスコアを有意に向上させるか。
- 被験者: 大学生
- 研究デザイン:
- まず、参加者全員に短期記憶テスト(単語リストの記憶テスト)を実施し、ベースラインのスコアを測定します(事前テスト)。
- 次に、参加者全員が1週間の記憶術トレーニングプログラムを受講します。
- プログラム終了後、事前テストと同形式の短期記憶テストを再度実施します(事後テスト)。
- 各参加者の「事後テストのスコア – 事前テストのスコア」という差分を算出し、この差分の平均が0より大きいかを検証します。
サンプルサイズ設計のためのパラメータ設定:
- 有意水準 (α): 慣例に従い
0.05(片側検定、スコアが「向上する」ことを期待するため)に設定します。 - 検出力 (1 – β): トレーニングに本当に効果がある場合、それを80%の確率で検出できるように
0.80に設定します。 - 効果量 (d_z):
- 過去の類似研究から、テストスコアの差分の標準偏差 (σ_diff) は約 8点 であることが分かっています。
- 研究者は、教育的に意味のある変化として、トレーニングによって平均 4点 スコアが向上すれば、このプログラムは有効であると判断します。これが検出したい差分の平均 (μ_diff) です。
- したがって、効果量
d_z = |μ_diff| / σ_diff = 4 / 8 = 0.5(中程度の効果量)を検出したいと考えます。
このシナリオに基づき、「この研究には何人の大学生に参加してもらう必要があるか?」を計算し、シミュレーションで検証します。
各パラメータの意味
- 有意水準 (α, alpha)
- 帰無仮説(H₀: 差分の母平均は0である, μ_diff = 0)は棄却されるべきではないにもかかわらず、それを棄却してしまう確率。
- 一般的に
α = 0.05に設定されますが、目的により異なります。
- 検出力 (Power, 1 – β)
- 対立仮説(H₁: 差分の母平均は0ではない, μ_diff ≠ 0)が真であるときに、それを正しく検出できる確率。
- 一般的に
1 - β = 0.80や0.90に設定されますが、目的により異なります。
- 効果量 (Effect Size, d_z)
- 検出したい差の大きさを示す標準化された指標です。対応のあるt検定では、差分の平均を差分の標準偏差で割った値を用います。
-
d_z = |μ_diff| / σ_diff-
μ_diff: 検出したい差分の母平均(例: 介入によって変化させたい平均的な量)。 -
σ_diff: 差分の母標準偏差。個体間の反応のばらつきを示します。
-
- 注意点: 対応なしt検定では元のデータの標準偏差
σを用いますが、対応のあるt検定では差分の標準偏差σ_diffを用いる点が異なります。個人内の変動が相殺されるため、通常σ_diffは元のデータのσよりも小さくなり、より小さいサンプルサイズで同じ効果量を検出できます。
- サンプルサイズ (n)
- 必要な被験者の数(ペアの数)です。これを求めます。
対応のあるt検定 (Paired t-test) は、2つの群のデータ(例: 介入前と介入後)を直接比較するのではなく、各個体における差分 (difference) について検定します。
具体的には、各個体の「介入後の値 – 介入前の値」という差分のデータセットを作成し、その差分の母平均が0と有意に異なるかどうかを検定します。
つまり、対応のあるt検定は、実質的に「差分のデータ」に対する「1標本のt検定 (One-sample t-test)」と等価であり、上記パラメータの関係性は、検定統計量t値が従う非心t分布によって結びついています。
2. R言語によるシミュレーションコード
まず、必要なライブラリを読み込みます。
library(pwr)
library(ggplot2)
library(dplyr)
library(MASS) # 多変量正規分布のデータを生成するために使用
seed <- 20250708ステップ1: シナリオに基づいたサンプルサイズの計算
Rのpwrパッケージにあるpwr.t.test関数で、type = "paired"を指定して計算します。
cat("--- ステップ1: サンプルサイズの計算 ---\n")
# パラメータ設定
effect_size_dz <- 0.5 # 差分の効果量 d_z
sig_level <- 0.05 # 有意水準 alpha
power_level <- 0.80 # 検出力 1-beta
# サンプルサイズの計算
# nをNULLにすることで、必要なサンプルサイズを計算させる
sample_size_calc <- pwr.t.test(
d = effect_size_dz,
sig.level = sig_level,
power = power_level,
type = "paired", # 対応のあるt検定
alternative = "greater" # 片側検定(スコアの向上を期待)
)
# 結果の表示
print(sample_size_calc)
# 必要なサンプルサイズ(被験者数)を取得(切り上げ)
n_required <- ceiling(sample_size_calc$n)
cat("\n")
cat(paste0("結論: この研究には最低 ", n_required, " 人の参加者が必要です。\n"))--- ステップ1: サンプルサイズの計算 ---
Paired t test power calculation
n = 26.13753
d = 0.5
sig.level = 0.05
power = 0.8
alternative = greater
NOTE: n is number of *pairs*
結論: この研究には最低 27 人の参加者が必要です。計算結果から、この研究には27人の参加者が必要であることがわかります。
ステップ2: 検出力のシミュレーション (対立仮説が真の場合)
計算で得られたサンプルサイズ(27人)を用いて、本当に検出力が80%程度になるかシミュレーションで確認します。対応のあるデータを生成するため、事前スコアと事後スコアに相関を持たせます。
cat("--- ステップ2: 検出力のシミュレーション ---\n")
# シミュレーションのパラメータ設定
set.seed(seed) # 結果を再現可能にする
n_sim <- 10000 # シミュレーション回数
# シナリオの母集団パラメータ
mean_pre <- 50 # 事前テストの平均スコア
sd_diff <- 8 # 差分の標準偏差
mean_diff <- 4 # 期待される差分の平均 (4点向上)
mean_post <- mean_pre + mean_diff # 事後テストの平均スコア
# データ生成のための相関パラメータを設定
# (sd_diff^2 = sd_pre^2 + sd_post^2 - 2*rho*sd_pre*sd_post の関係を利用)
sd_pre <- 10 # 事前スコアの標準偏差を仮定
sd_post <- 10 # 事後スコアの標準偏差を仮定
# 相関係数 rho を逆算
rho <- (sd_pre^2 + sd_post^2 - sd_diff^2) / (2 * sd_pre * sd_post)
# 平均ベクトルと共分散行列
mu_vector <- c(mean_pre, mean_post)
sigma_matrix <- matrix(
c(
sd_pre^2, rho * sd_pre * sd_post,
rho * sd_pre * sd_post, sd_post^2
),
nrow = 2
)
# 結果を格納するベクトル
p_values_h1 <- numeric(n_sim)
# シミュレーションループ
for (i in 1:n_sim) {
# 1. 対立仮説が真である状況の相関のあるデータを生成
# (mvrnorm: 多変量正規分布から乱数生成)
paired_data <- mvrnorm(n = n_required, mu = mu_vector, Sigma = sigma_matrix)
# 2. 対応のあるt検定を実行
t_test_result <- t.test(paired_data[, 2], paired_data[, 1],
paired = TRUE, alternative = "greater"
)
# 3. p値を保存
p_values_h1[i] <- t_test_result$p.value
}
# シミュレーションによる検出力の計算
simulated_power <- mean(p_values_h1 < sig_level)
cat(paste0("\nシミュレーションによる検出力: ", round(simulated_power, 3), "\n"))--- ステップ2: 検出力のシミュレーション ---
シミュレーションによる検出力: 0.815シミュレーション結果は、目標とした検出力0.80に近い値(約0.815)となり、サンプルサイズ設計の妥当性が裏付けられました。
ステップ3: 検出力シミュレーション結果の可視化
cat("--- ステップ3: 検出力シミュレーション結果の可視化 ---\n")
p_values_df_h1 <- data.frame(p_value = p_values_h1)
plot_power <- ggplot(p_values_df_h1, aes(x = p_value)) +
geom_histogram(binwidth = 0.05, fill = "skyblue", color = "black", boundary = 0) +
geom_vline(xintercept = sig_level, color = "red", linetype = "dashed", linewidth = 1) +
annotate("text",
x = 0.5, y = 4500,
label = paste("シミュレーションによる検出力 (p < 0.05) =", round(simulated_power, 3)),
color = "red", size = 5
) +
labs(
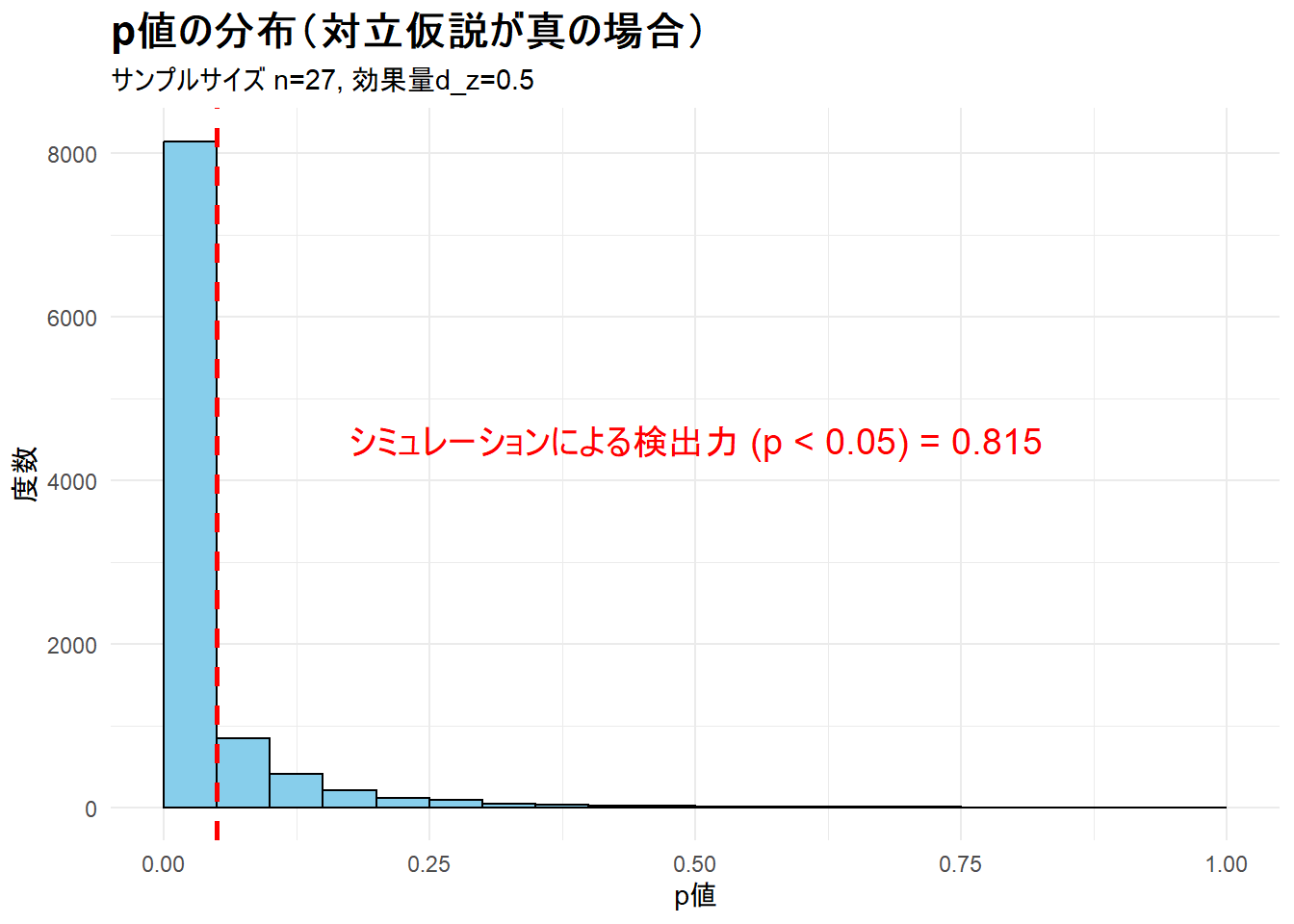
title = "p値の分布(対立仮説が真の場合)",
subtitle = paste0("サンプルサイズ n=", n_required, ", 効果量d_z=", effect_size_dz),
x = "p値",
y = "度数"
) +
theme_minimal() +
theme(plot.title = element_text(size = 16, face = "bold"))
print(plot_power)--- ステップ3: 検出力シミュレーション結果の可視化 ---Figure 1 からp値が0に近い方に偏っており、有意水準0.05を下回る割合が約80%であることを視覚的に確認できます。
ステップ4: 第1種の過誤のシミュレーション (帰無仮説が棄却されない場合)
次に、トレーニングに全く効果がなかった場合(帰無仮説が棄却されない)に、誤って「効果あり」と結論づけてしまう確率(第1種の過誤率)が、設定した有意水準α (0.05)と一致するかを確認します。
cat("--- ステップ4: 第1種の過誤のシミュレーション ---\n")
# 帰無仮説が棄却されない場合 (平均に差がない)
mu_vector_h0 <- c(mean_pre, mean_pre) # 事後も平均は同じ
p_values_h0 <- numeric(n_sim)
for (i in 1:n_sim) {
paired_data_h0 <- mvrnorm(n = n_required, mu = mu_vector_h0, Sigma = sigma_matrix)
t_test_result_h0 <- t.test(paired_data_h0[, 2], paired_data_h0[, 1],
paired = TRUE, alternative = "greater"
)
p_values_h0[i] <- t_test_result_h0$p.value
}
type1_error_rate <- mean(p_values_h0 < sig_level)
cat(paste("\nシミュレーションによる第1種の過誤率:", round(type1_error_rate, 3), "\n"))--- ステップ4: 第1種の過誤のシミュレーション ---
シミュレーションによる第1種の過誤率: 0.047 シミュレーションによる第1種の過誤率は、設定した有意水準0.05に近い値(約0.047)となり、検定が正しく機能していることがわかります。
ステップ5: 第1種の過誤シミュレーション結果の可視化
cat("\n--- ステップ5: 第1種の過誤シミュレーション結果の可視化 ---\n")
p_values_df_h0 <- data.frame(p_value = p_values_h0)
expected_freq <- n_sim * 0.05
plot_alpha <- ggplot(p_values_df_h0, aes(x = p_value)) +
geom_histogram(binwidth = 0.05, fill = "lightcoral", color = "black", boundary = 0) +
geom_vline(xintercept = sig_level, color = "blue", linetype = "dashed", linewidth = 1) +
geom_hline(yintercept = expected_freq, color = "darkgreen", linetype = "dotted", linewidth = 1) +
annotate("text",
x = 0.5, y = 600,
label = paste("第1種の過誤の確率 (p < 0.05) =", round(type1_error_rate, 3)),
color = "blue", size = 5
) +
labs(
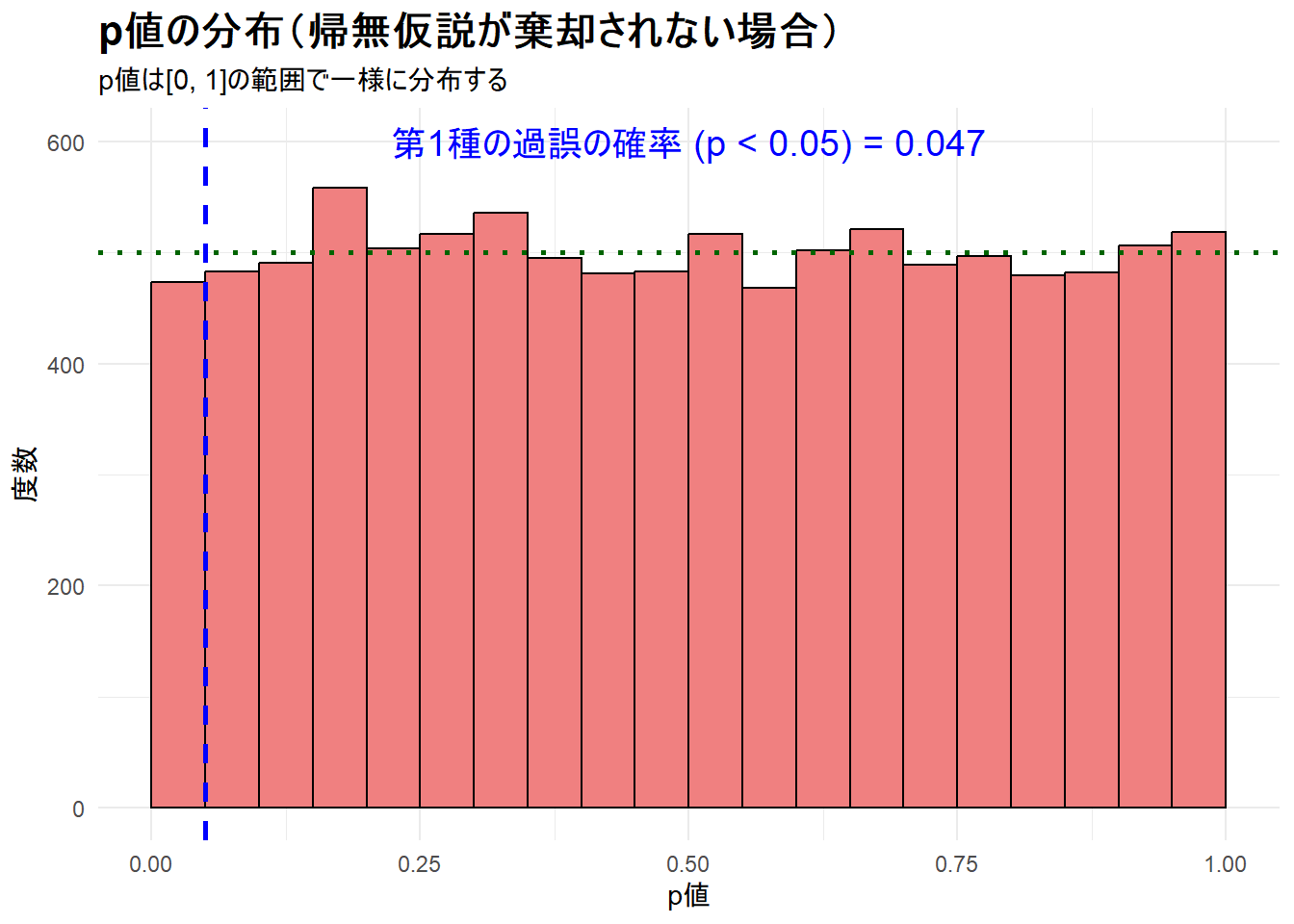
title = "p値の分布(帰無仮説が棄却されない場合)",
subtitle = "p値は[0, 1]の範囲で一様に分布する",
x = "p値",
y = "度数"
) +
theme_minimal() +
theme(plot.title = element_text(size = 16, face = "bold"))
print(plot_alpha)
--- ステップ5: 第1種の過誤シミュレーション結果の可視化 ---Figure 2 は、p値がほぼフラットな分布を示しており、これにより、偶然だけで有意な差が出る確率が、意図通り5%にコントロールされていることが視覚的に確認できます。
以上です。