Rでチェビシェフの不等式

チェビシェフの不等式とは

チェビシェフの不等式は、確率分布の種類によらず（どんな形のデータ分布であっても）、データがその平均値からどの程度ばらついているか（離れているか）の確率の上限を与える定理です。

具体的には、確率変数 \(X\) の平均を \(\mu\)、標準偏差を \(\sigma\) としたとき、任意の正の実数 \(k\) (\(k>0\)) に対して、以下の関係が成り立ちます。

\[ P(|X - \mu| \geq k\sigma) \leq \frac{1}{k^2} \]

この式が意味することは以下の通りです。

• 左辺: \(|X - \mu| \geq k\sigma\) は、「データ（\(X\)）が平均（\(\mu\)）から \(k\) 標準偏差（\(k\sigma\)）以上離れている」という事象を表します。\(P(...)\) はその事象が起こる確率です。
• 右辺: \(\frac{1}{k^2}\) は、その確率の上限値（これより大きくはならないという限界の値）です。

簡単な例

• k=2 の場合: データが平均から2標準偏差以上離れている確率は、\(\frac{1}{2^2} = \frac{1}{4} = 25\%\) 以下である。
• k=3 の場合: データが平均から3標準偏差以上離れている確率は、\(\frac{1}{3^2} = \frac{1}{9} \approx 11.1\%\) 以下である。

この不等式の重要な点の1つは、「あらゆる確率分布に対して成り立つ」という普遍性です。データが正規分布のように綺麗な釣鐘型でなくても、歪んだ分布や未知の分布であっても、この関係は保証されます。

R言語によるシミュレーション

それでは、この不等式が実際に成り立つことをR言語でシミュレーションしてみましょう。 ここでは、以下の2種類の異なる分布からサンプルデータを生成し、それぞれでチェビシェフの不等式が成立することを確認します。

1. 正規分布: 左右対称の釣鐘型の分布
2. 指数分布: 右に裾が長い（歪んだ）非対称な分布

# データ操作とプロットのためのライブラリを読み込み
library(dplyr)
library(ggplot2)
library(purrr) # map_dbl関数を利用するために読み込み

seed <- 20250707

# シミュレーションのパラメータ設定
n_samples <- 10000 # サンプルサイズ
k_values <- seq(1.2, 4.0, by = 0.2) # 検証するkの値（1.2から4.0まで0.2刻み）

# 再現性のために乱数シードを固定
set.seed(seed)

# ---- データ生成 ----
# 正規分布データ
data_norm <- rnorm(n_samples, mean = 10, sd = 3)
# 指数分布データ
data_exp <- rexp(n_samples, rate = 0.5)

# ---- シミュレーションを実行する関数を定義----
run_simulation <- function(data, k_values, dist_name) {
  mu <- mean(data)
  sigma <- sd(data)
  n <- length(data)

  # kの各値について計算を行う
  tibble(k = k_values) %>%
    mutate(
      # purrr::map_dblを使い、kの各要素に対して計算を適用する
      # .x に k_values の値が一つずつ入る
      actual_prob = map_dbl(k, ~ sum(abs(data - mu) >= .x * sigma) / n),
      chebyshev_bound = 1 / k^2,
      distribution = dist_name
    )
}

# ---- 各分布でシミュレーションを実行 ----
results_norm <- run_simulation(data_norm, k_values, "正規分布")
results_exp <- run_simulation(data_exp, k_values, "指数分布")

# 2つの結果を1つのデータフレームに結合
all_results <- bind_rows(results_norm, results_exp)

cat("--- 結果の確認 ---\n")
print.data.frame(all_results, max = NULL)

--- 結果の確認 ---
     k actual_prob chebyshev_bound distribution
1  1.2      0.2323      0.69444444     正規分布
2  1.4      0.1591      0.51020408     正規分布
3  1.6      0.1070      0.39062500     正規分布
4  1.8      0.0710      0.30864198     正規分布
5  2.0      0.0441      0.25000000     正規分布
6  2.2      0.0292      0.20661157     正規分布
7  2.4      0.0157      0.17361111     正規分布
8  2.6      0.0093      0.14792899     正規分布
9  2.8      0.0048      0.12755102     正規分布
10 3.0      0.0030      0.11111111     正規分布
11 3.2      0.0016      0.09765625     正規分布
12 3.4      0.0008      0.08650519     正規分布
13 3.6      0.0003      0.07716049     正規分布
14 3.8      0.0002      0.06925208     正規分布
15 4.0      0.0000      0.06250000     正規分布
16 1.2      0.1072      0.69444444     指数分布
17 1.4      0.0869      0.51020408     指数分布
18 1.6      0.0696      0.39062500     指数分布
19 1.8      0.0586      0.30864198     指数分布
20 2.0      0.0473      0.25000000     指数分布
21 2.2      0.0393      0.20661157     指数分布
22 2.4      0.0325      0.17361111     指数分布
23 2.6      0.0273      0.14792899     指数分布
24 2.8      0.0220      0.12755102     指数分布
25 3.0      0.0182      0.11111111     指数分布
26 3.2      0.0154      0.09765625     指数分布
27 3.4      0.0132      0.08650519     指数分布
28 3.6      0.0106      0.07716049     指数分布
29 3.8      0.0095      0.06925208     指数分布
30 4.0      0.0086      0.06250000     指数分布

4. 結果の可視化

シミュレーション結果をプロットすることで、関係性をより直感的に理解できます。ここでは、「実際の確率」と「チェビシェフの上限」をkの値に対してプロットします。

# ggplotで結果を可視化
ggplot(all_results, aes(x = k)) +
  # チェビシェフの上限を線で描画 (理論値)
  geom_line(aes(y = chebyshev_bound, color = "チェビシェフの上限 (1/k²)"), linewidth = 1.2) +
  # 実際の確率を点で描画 (シミュレーション結果)
  geom_point(aes(y = actual_prob, color = "実際の確率"), size = 3) +
  # グラフを分布の種類ごとに分ける
  facet_wrap(~distribution) +
  # 凡例、タイトル、軸ラベルを設定
  scale_color_manual(
    name = "凡例",
    values = c("チェビシェフの上限 (1/k²)" = "red", "実際の確率" = "blue")
  ) +
  scale_y_continuous(labels = scales::percent_format()) + # y軸をパーセント表示に
  labs(
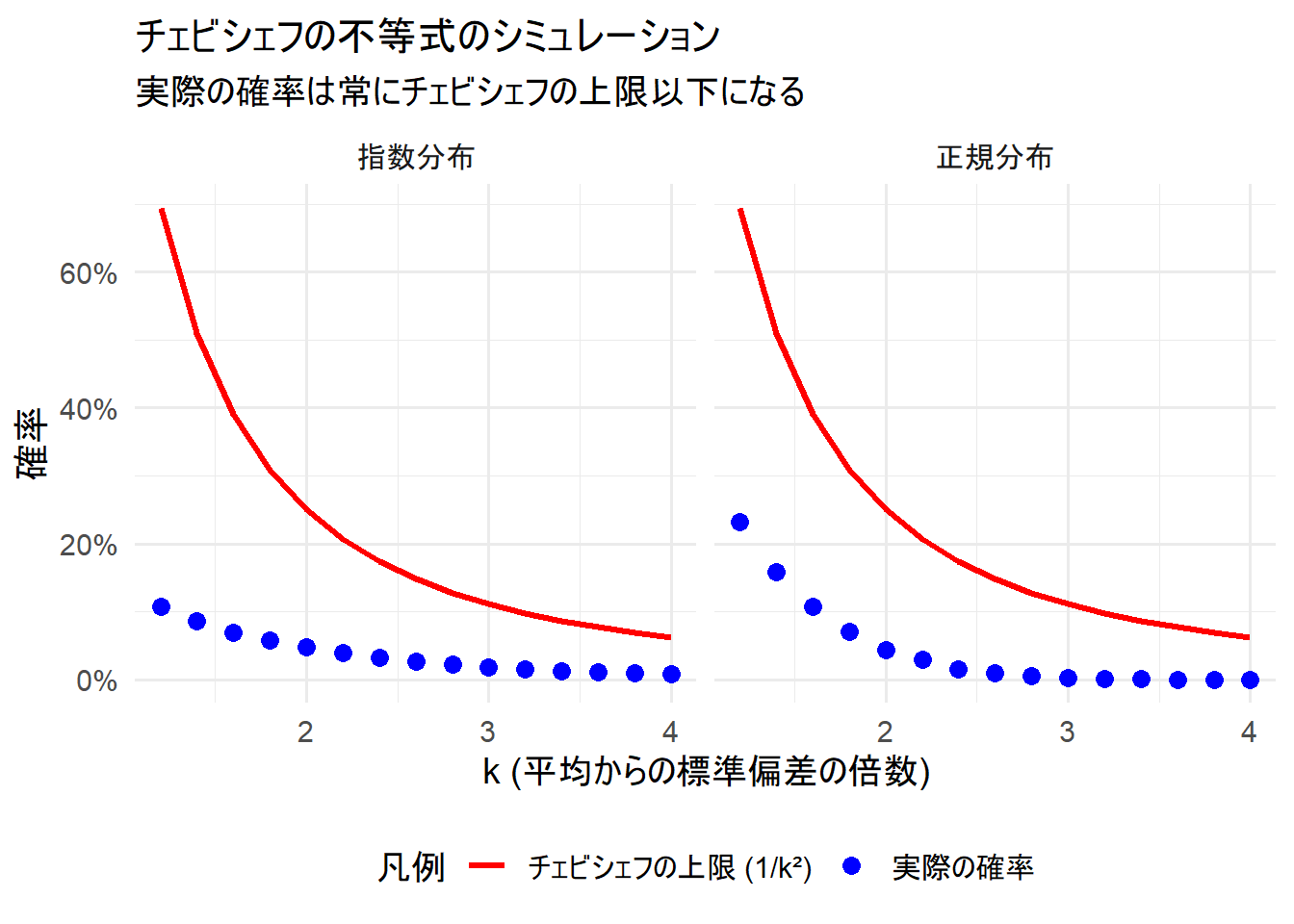
    title = "チェビシェフの不等式のシミュレーション",
    subtitle = "実際の確率は常にチェビシェフの上限以下になる",
    x = "k (平均からの標準偏差の倍数)",
    y = "確率"
  ) +
  theme_minimal(base_size = 14) +
  theme(legend.position = "bottom")

プロットの解説

Figure 1 から、「正規分布」、「指数分布」のどちらにおいても、青い点（実際の確率）が常に赤い線（チェビシェフの上限）の下にあることを確認できます。

さらに、2つの分布を比較すると、以下の点も確認できます。

1. 一見したときの印象と、その理由

プロットを単純に見ると、指数分布の青い点の方が、正規分布の点よりも赤い線から大きく離れている（＝確率が低い）ように見えます。これはなぜでしょうか？

原因は、チェビシェフの不等式が「両側」の確率を評価するのに対し、指数分布が「非対称」な分布であることにあります。

• チェビシェフの不等式: 平均 \(\mu\) から「左右両方に」\(k\sigma\) 以上離れたデータの割合を見ています。
• 正規分布: 左右対称なため、平均の両側に均等に確率が分布しています。
• 指数分布: 0未満の値を取らない右に歪んだ分布です。そのため、平均から左側に離れた領域（μ - kσ が負になる場合など）にはデータが存在せず、実際の確率は実質的に右側の裾（平均より大きい値）の確率だけで計算されます。

このため、特にkが小さい領域では、両側の確率を持つ正規分布に比べて、片側しか寄与しない指数分布の実際の確率が低く見えるのです。

2. 「裾の重さ」はどこに現れるか？

では、「指数分布は裾が重い（極端な値が出やすい）」という性質はどこに現れているのでしょうか。それは、kが大きくなる領域（グラフの右側）に注目すると分かります。

• 正規分布（裾が軽い）: kが大きくなるにつれて、実際の確率は急激に0に近づきます。k=3 を超えると、該当するデータはほとんどなくなります（k=4で0%）。
• 指数分布（裾が重い）: kが大きくなっても、確率は正規分布より緩やかにしか減少しません。k=4 の時点でも、依然として0.86%の確率でデータが存在しています。

これは、「平均から極端に離れた値」が、正規分布よりも指数分布の方が出現しやすいことを意味しています。これが「裾が重い」という性質の本質です。

以上です。