Rで因子分析

Rで 因子分析 を試みます。

本ポストはこちらの続きです。

Rで主成分分析を試みます。1. 主成分分析とは主成分分析（Principal Component Analysis, PCA）は、多変量解析の手法の一つです。多数の変量（量的変数）からなるデータを、より少ない指標（主成分）に要約すること...

1. 因子分析とは

因子分析（Factor Analysis）は、多変量解析の手法の一つで、観測された多数の変数（例：テストの各設問への回答）の背後に存在する、直接観測できない潜在的な共通因子（例：論理的思考力、言語能力）を見つけ出すことを目的とします。

主成分分析が観測変数の分散をできるだけ要約することを目指すのに対し、因子分析は観測変数間の相関関係を説明しようと試みます。つまり、「なぜ、これらの変数は互いに相関しているのか？」という問いに、「それらの背後に共通の原因（因子）があるからだ」と仮定して、その構造を探る手法です。

数学的なモデルは以下のように表されます。

x = Λf + ε

ここで、

x: 観測された変数（p個）のベクトル。
Λ (ラムダ): 因子負荷量行列 (Factor Loading Matrix)。観測変数と共通因子の間の相関の強さを示す行列です。この値が大きいほど、その観測変数がその共通因子を強く反映していることを意味します。
f: 共通因子 (Common Factor)。観測変数群に共通して影響を与える潜在的な因子（k個, k < p）のベクトル。
ε (イプシロン): 独自因子 (Unique Factor)。各観測変数にのみ影響を与える部分（測定誤差など）のベクトル。

このモデルに基づき、各観測変数の分散は以下のように分解できます。

Var(x_i) = (共通性) + (独自性)

共通性 (Communality, h²): 観測変数 x_i の分散のうち、すべての共通因子 f によって説明される部分の割合。
独自性 (Uniqueness, u²): 観測変数 x_i の分散のうち、その変数に固有の独自因子 ε_i によってのみ説明される部分の割合。

標準化されたデータでは、各変数の分散は1ですので、共通性(h²) + 独自性(u²) = 1 となります。

因子分析のプロセス

相関行列の算出: 観測変数間の相関行列を計算します。因子分析の出発点となります。
因子数の決定: いくつの共通因子を抽出するかを決定します。平行分析（Parallel Analysis）やスクリープロット、MAPテストなどの手法が用いられます。
因子負荷量の推定: 共通性を考慮しながら、因子負荷量行列 Λ を推定します。主な推定法に、最尤法、主因子法、最小残差法などがあります。
因子の回転: 推定された因子負荷量は、そのままでは解釈が難しいことが多いです。そのため、各変数が特定の因子に強く負荷し、他の因子には弱く負荷するように軸を回転させ、解釈しやすい単純な構造を目指します。
- 直交回転（例: バリマックス法）: 因子間の相関を0と仮定して回転します。因子同士が独立であると考えられる場合に使用します。
- 斜交回転（例: プロマックス法, オブリミン法）: 因子間の相関を許容して回転します。心理学的な構成概念など、因子同士に関連があると考えられる場合に使用します。
解釈と因子得点の算出: 回転後の因子負荷量行列をもとに各因子が何を意味するのかを解釈します。必要に応じて、各サンプルの因子得点（その人が各因子をどの程度持っているかを示すスコア）を計算します。

2. シミュレーションのシナリオ

シナリオ: 「新しい性格検査尺度の構造を探る」

ある心理学研究室が、現代人の働き方における性格特性を測定するための新しい心理尺度を開発しました。この尺度は、理論的には以下の3つの潜在的な性格特性（因子）を測定することを意図して作られています。

計画性 (Planning): 物事を順序立てて計画的に進める能力。
協働性 (Collaboration): 他者と協力し、円滑な人間関係を築く能力。
革新性 (Innovation): 新しいアイデアを生み出し、変化を恐れない姿勢。

この理論的な構造が、実際のデータでも支持されるかを確認するため、200人の社会人を対象に、10項目の質問（各特性に対応）に5段階（1: 全く当てはまらない〜 5: 非常に当てはまる）で回答してもらいました。

目的: 因子分析を用いて、この10項目が本当に想定通りの3つの因子（計画性、協働性、革新性）に分類されるのか、その背後にある構造を検証します。

想定されるデータ構造:

計画性に関連する項目群（Q1, Q2, Q3）は、互いに強い相関を持つ。
協働性に関連する項目群（Q4, Q5, Q6）は、互いに強い相関を持つ。
革新性に関連する項目群（Q7, Q8, Q9, Q10）は、互いに強い相関を持つ。
異なる特性を測る項目群間の相関は、上記に比べて弱い。
性格特性なので、3つの因子間にはある程度の相関があるかもしれません（例：計画性が高い人は協働性も少し高い傾向があるなど）。そのため、因子間に相関を許す「斜交回転」が適していると予想されます。

3. R言語によるシミュレーション

0. シナリオに基づいたサンプルデータの生成

library(psych)
library(ggplot2)
library(dplyr)
library(ggrepel)

seed <- 20250724
set.seed(seed) # 結果の再現性を確保

# 因子構造を定義する負荷量行列を作成
# 3つの因子（計画性, 協働性, 革新性）と10個の質問項目
fx <- matrix(c(
  # 計画性, 協働性, 革新性  (←因子)
  0.8, 0.1, 0.1, # Q1
  0.7, 0.0, 0.2, # Q2
  0.6, 0.2, 0.0, # Q3
  0.1, 0.8, 0.1, # Q4
  0.0, 0.7, 0.0, # Q5
  0.2, 0.6, 0.2, # Q6
  0.1, 0.0, 0.8, # Q7
  0.0, 0.1, 0.7, # Q8
  0.2, 0.0, 0.6, # Q9
  0.1, 0.2, 0.5 # Q10
), ncol = 3, byrow = TRUE)

# 因子間の相関を少しだけ設定（性格特性は完全に独立ではないため）
Phi <- matrix(c(
  1.0, 0.3, 0.2,
  0.3, 1.0, 0.25,
  0.2, 0.25, 1.0
), ncol = 3, byrow = TRUE)

# sim.structure関数で意図した構造のデータを生成
# これにより、共通性が1を超えるヘイウッドケースが発生しにくい
sim_data <- sim.structure(fx = fx, Phi = Phi, n = 200)
sample_data <- sim_data$observed
colnames(sample_data) <- paste0("Q", 1:10)

cat("--- 生成されたサンプルデータの一部を確認 ---\n\n")
print(head(round(sample_data, 2)))
print(tail(round(sample_data, 2)))

--- 生成されたサンプルデータの一部を確認 ---

        Q1    Q2    Q3    Q4    Q5    Q6    Q7    Q8    Q9   Q10
[1,]  0.00  0.57  0.68 -0.38 -0.30 -1.12 -0.64 -0.99  0.07 -1.69
[2,] -0.89 -2.03 -2.42 -0.47 -0.17  1.12  0.73  1.63 -0.35  0.08
[3,] -0.40 -0.43 -0.13  0.30 -0.26  0.32  0.91  1.78  0.28  1.96
[4,] -0.62 -0.19 -0.17  1.09 -0.81 -0.98 -1.04  0.06 -0.50  0.26
[5,] -0.96  0.72  1.11  0.75  1.28  0.65 -0.27 -0.37 -0.04  0.83
[6,]  0.73  0.61  1.52  0.58  0.20 -1.27  0.00  0.17  0.46 -0.28
          Q1    Q2    Q3    Q4    Q5    Q6    Q7    Q8    Q9   Q10
[195,] -0.49  1.56  0.32  2.05  0.73  1.04  0.68  0.65 -0.11  2.74
[196,]  0.81  1.33  0.58 -0.38 -0.08  1.00  0.43  1.46  1.78  0.66
[197,]  0.35  0.14 -0.66 -1.08 -0.39 -1.14 -0.10 -0.93 -0.29 -0.55
[198,]  1.22 -0.50  1.85  0.46  0.29  0.54  1.15 -0.09 -0.18 -0.26
[199,] -1.83 -1.65 -1.93 -0.08 -0.78 -0.07  0.29  0.01 -0.10  1.11
[200,] -1.24 -0.83 -0.44 -0.24 -0.89 -0.52 -1.22 -0.50 -1.68 -1.37

1. 因子数の決定（平行分析）

# 平行分析を実行してプロット

set.seed(seed)

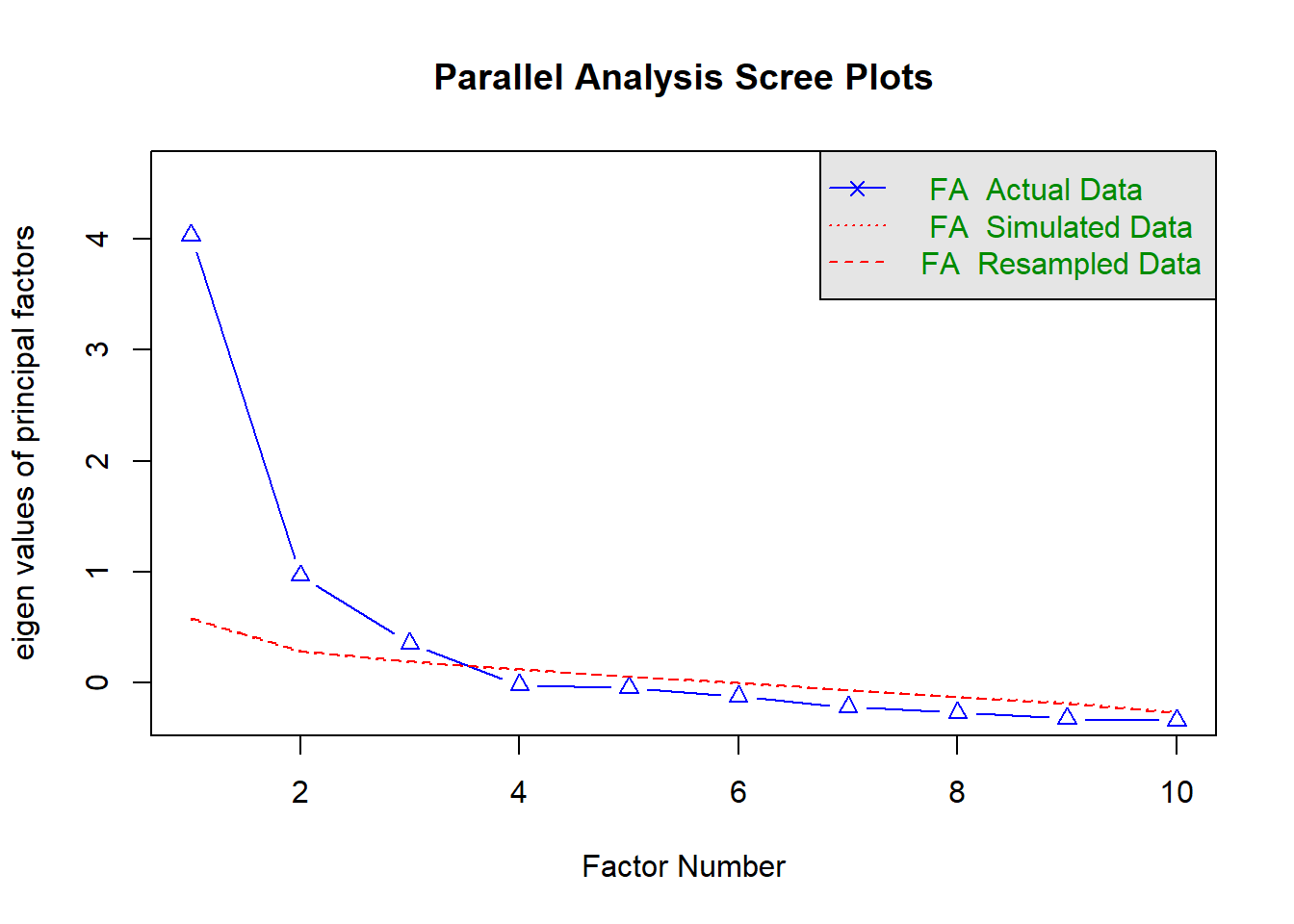
fa_parallel_result <- fa.parallel(sample_data, fa = "fa", fm = "minres")

print(fa_parallel_result)

Call: fa.parallel(x = sample_data, fm = "minres", fa = "fa")
Parallel analysis suggests that the number of factors =  3  and the number of components =  NA 

 Eigen Values of 

 eigen values of factors
 [1]  4.03  0.97  0.36 -0.02 -0.05 -0.12 -0.22 -0.27 -0.32 -0.34

 eigen values of simulated factors
 [1]  0.58  0.28  0.19  0.12  0.05  0.00 -0.07 -0.12 -0.18 -0.26

 eigen values of components 
 [1] 4.60 1.63 0.94 0.62 0.52 0.45 0.33 0.33 0.30 0.28

 eigen values of simulated components
[1] NA

平行分析の結果、実際のデータの固有値（eigen values of factors。青線）が、ランダムデータの平均固有値（eigen values of simulated factors。赤線）を上回っている成分の数は「3つ」であることが示唆されました。

これは、シナリオで想定した3因子構造と一致します。したがって、因子数を3として分析を進めます。

2. 因子分析の実行

# fa関数で因子分析を実行
# fm="minres": 最小残差法（頑健な推定法）
# rotate="oblimin": 斜交回転（因子間の相関を許容）
fa_result <- fa(sample_data, nfactors = 3, fm = "minres", rotate = "oblimin")

cat("因子分析の結果（主要部分）:\n\n")
# 結果を見やすく表示 (cut=0.3で、負荷量の絶対値が0.3未満のものは表示しない)
print(fa_result, digits = 2, cut = 0.3, sort = TRUE)

因子分析の結果（主要部分）:

Factor Analysis using method =  minres
Call: fa(r = sample_data, nfactors = 3, rotate = "oblimin", fm = "minres")
Standardized loadings (pattern matrix) based upon correlation matrix
    item   MR2   MR3   MR1   h2   u2 com
Q7     7  0.89             0.78 0.22 1.0
Q8     8  0.70             0.54 0.46 1.1
Q10   10  0.56             0.50 0.50 1.4
Q9     9  0.54             0.39 0.61 1.6
Q1     1        0.89       0.82 0.18 1.0
Q3     3        0.70       0.50 0.50 1.0
Q2     2        0.64       0.53 0.47 1.2
Q4     4              0.84 0.74 0.26 1.0
Q5     5              0.76 0.53 0.47 1.0
Q6     6              0.58 0.69 0.31 1.5

                       MR2  MR3  MR1
SS loadings           2.14 1.96 1.91
Proportion Var        0.21 0.20 0.19
Cumulative Var        0.21 0.41 0.60
Proportion Explained  0.36 0.33 0.32
Cumulative Proportion 0.36 0.68 1.00

 With factor correlations of 
     MR2 MR3  MR1
MR2 1.00 0.3 0.51
MR3 0.30 1.0 0.60
MR1 0.51 0.6 1.00

Mean item complexity =  1.2
Test of the hypothesis that 3 factors are sufficient.

df null model =  45  with the objective function =  4.66 with Chi Square =  907.45
df of  the model are 18  and the objective function was  0.08 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.03 

The harmonic n.obs is  200 with the empirical chi square  5.94  with prob <  1 
The total n.obs was  200  with Likelihood Chi Square =  15.57  with prob <  0.62 

Tucker Lewis Index of factoring reliability =  1.007
RMSEA index =  0  and the 90 % confidence intervals are  0 0.054
BIC =  -79.8
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   MR2  MR3  MR1
Correlation of (regression) scores with factors   0.93 0.94 0.93
Multiple R square of scores with factors          0.86 0.87 0.86
Minimum correlation of possible factor scores     0.73 0.75 0.72

3. 結果の解釈

因子負荷量 (MR2, MR3, MR1 の列)

MR2 (第1の因子): Q7, Q8, Q9, Q10が高い負荷量(0.89~0.54)を示しており、「革新性」因子と解釈できます。
MR3 (第2の因子): Q1, Q2, Q3が高い負荷量(0.89~0.64)を示しており、「計画性」因子と解釈できます。
MR1 (第3の因子): Q4, Q5, Q6が高い負荷量(0.84~0.58)を示しており、「協働性」因子と解釈できます。
結果として想定通りの3つの因子グループが明確に抽出されました。

共通性 (h2)

各項目が、抽出された3つの共通因子によってどれだけ説明されているかを示します。
例えば、Q7のh2が0.78ということは、Q7の回答のばらつきの78%が3つの因子で説明できることを意味します。

独自性 (u2)

1 - h2 の値であり、各項目に固有のばらつき（測定誤差など）の割合を示します。

因子間相関 (With factor correlations of)

抽出された3つの因子間の相関です。例えば、MR3(計画性)とMR1(協働性)の相関は0.60と、中程度の正の相関があることがわかります。
また、MR2(革新性)とMR1(協働性)の相関は0.51、MR2(革新性)とMR3(計画性)の相関は0.30となっています。
これは、これらの性格特性が完全に独立ではなく、互いに関連しあっていることを示唆しています。

適合度指標

RMSEA = 0 (90%CI: 0-0.054):
- モデルの適合度は良好であることを示します。
- よって、構築した3因子モデル（計画性、協働性、革新性）は、観測された10個の質問項目間の相関関係を、ほぼ説明できていると判断できます。
TLI = 1.007:
- こちらも良好な適合度を示します。
- よって、3因子モデルは、「10個の質問項目が互いに全く無関係である」とする独立モデルと比べて、データの構造を説明できている(改善されている)と判断できます。

結論

これらの指標から、今回仮定した3因子モデルは、観測されたデータに適合していると判断できます。

4. 結果の可視化

# 4a. パス図による可視化
# 因子と各項目の関係性を視覚的に表現したパス図を表示します。
# ラベルが結果と一致するように調整
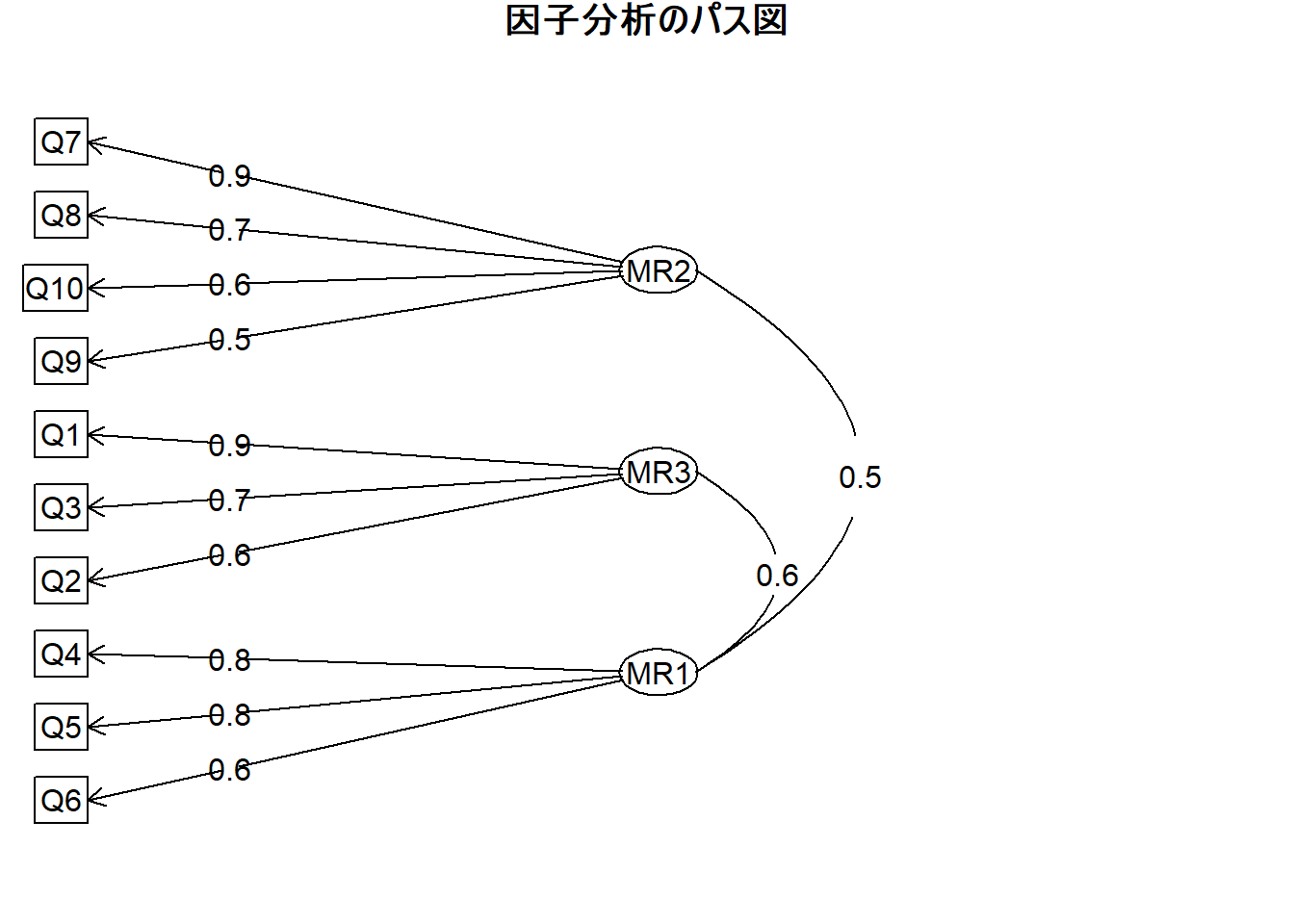
fa.diagram(fa_result,
  main = "因子分析のパス図",
  labels = c("革新性", "計画性", "協働性")
) # MR2, MR3, MR1 の順

# 4b. 因子負荷量プロット
# 因子1(協働性)と因子2(計画性)を軸として、各項目がどこに位置するかをプロットします。

# 因子負荷量を行列からデータフレームに変換
loadings_df <- as.data.frame(unclass(fa_result$loadings))
loadings_df$item <- rownames(loadings_df)

# プロット作成
loading_plot <- ggplot(loadings_df, aes(x = MR1, y = MR3, label = item)) +
  geom_point(color = "steelblue", size = 3) +
  geom_text_repel(size = 4, fontface = "bold") +
  geom_hline(yintercept = 0, linetype = "dashed", color = "gray50") +
  geom_vline(xintercept = 0, linetype = "dashed", color = "gray50") +
  labs(
    title = "因子負荷量プロット",
    subtitle = "協働性因子 vs 計画性因子",
    x = "協働性因子 (MR1) の負荷量",
    y = "計画性因子 (MR3) の負荷量"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(hjust = 0.5, face = "bold"),
    plot.subtitle = element_text(hjust = 0.5)
  )

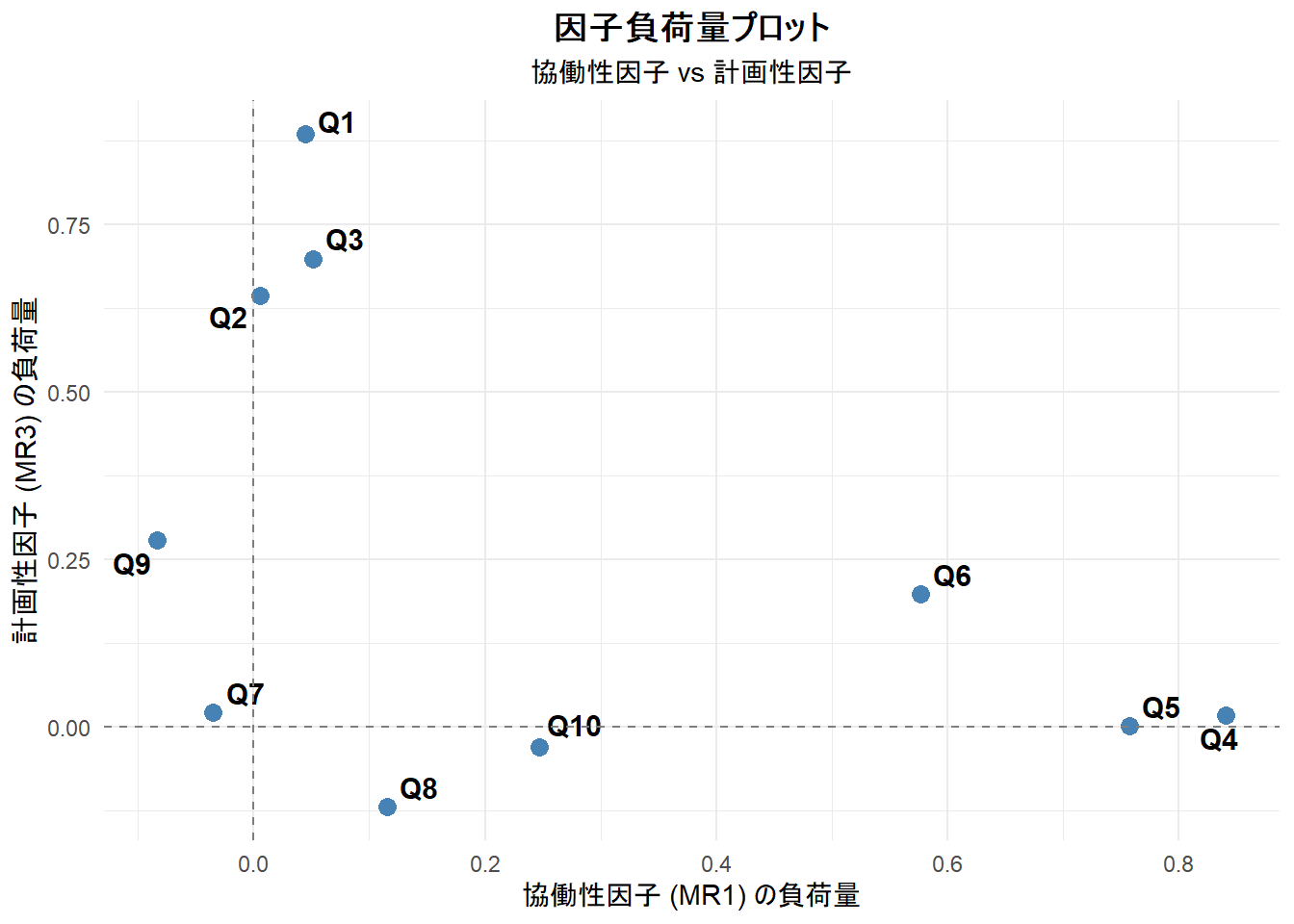
print(loading_plot)