Rで 微分方程式:確率微分方程式 を試みます。
本ポストはこちらの続きです。

1. 確率微分方程式の概要
1.1 確率微分方程式(SDE)とは?
一言でいうと、「予測不可能なランダムな揺らぎ(ノイズ)の影響を受けるシステムの振る舞い」を記述する微分方程式です。
これまでの常微分方程式(ODE)や偏微分方程式(PDE)は、初期値や条件が定まれば未来はただ一つに決まる「決定論的」な世界を扱っていました。しかし、現実世界の多くの現象(株価の変動、分子の拡散、生態系の変動など)は、予測不可能なランダムな要素に常に晒されています。SDEは、このような「確率論的」な振る舞いを数学的にモデル化するためのツールです。
SDEは一般的に以下の形で書かれます。
dX_t = a(t, X_t) dt + b(t, X_t) dW_t
-
X_t: 時刻tにおける確率的に変動する量(株価、粒子の位置など) -
a(t, X_t) dt: ドリフト項。システムの平均的な動きや傾向を表す決定論的な部分。ODEと同じような役割。 -
b(t, X_t) dW_t: 拡散項。ランダムな揺らぎの大きさを表す部分。 -
dW_t: ウィーナー過程(ブラウン運動)の微小な増分。これがランダム性の根源であり、正規分布に従うノイズとしてモデル化される。
1.2 ODE/PDEとの違い
| 項目 | 常微分方程式(ODE) / 偏微分方程式(PDE) | 確率微分方程式(SDE) |
|---|---|---|
| 性質 | 決定論的 | 確率論的 |
| 未来の予測 | 初期値が同じなら、未来は常に同じ経路をたどる。 | 初期値が同じでも、未来は毎回異なる経路をたどる。 |
| 解 | 1つの関数(曲線や曲面) | 確率過程(無数の可能性のある経路の集まり) |
| 興味の対象 | 一意に定まる解そのもの | 多数の経路(サンプルパス)の統計的な性質(平均、分散、確率分布など) |
| 含まれる項 | ドリフト項のみ | ドリフト項と拡散項(ランダムノイズ)の両方を含む |
1.3 具体例:幾何ブラウン運動
金融工学において、株価の変動モデルとして最も広く使われているSDEが「幾何ブラウン運動(Geometric Brownian Motion, GBM)」です。
dS_t = μ * S_t * dt + σ * S_t * dW_t
-
S_t: 時刻tにおける株価 -
μ: ドリフト率。株価の平均的な成長率(期待リターン)。 -
σ: ボラティリティ。株価の変動の激しさを表す。 -
μ * S_t * dt: 株価が複利のように平均的に成長していく部分。 -
σ * S_t * dW_t: ランダムなニュースなどによる価格変動。株価S_tが高いほど、変動額も大きくなるという現実的な性質を反映している。
1.4 数値解法:オイラー・丸山法
SDEをシミュレートするための数値解法の1つが「オイラー・丸山法」です。これはODEのオイラー法をSDEに拡張したものです。
微小時間 Δt 後の株価 S_{t+Δt} は、以下のように計算されます。
S_{t+Δt} ≈ S_t + μ * S_t * Δt + σ * S_t * ΔW_t
ここで、ランダムノイズの項 ΔW_t は、平均 0、分散 Δt の正規分布に従う乱数で近似します。これは、標準正規分布(平均0, 分散1)に従う乱数 Z を使って ΔW_t = Z * sqrt(Δt) と表現できます。
2. シミュレーションのためのRコード
それでは、Rで幾何ブラウン運動に従う株価のシミュレーションを行います。SDEのシミュレーションでは、たった1つの経路を見るだけでは意味がなく、多数のありうる未来(サンプルパス)を同時に生成して、そのばらつきを見ることが重要です。
2.1 準備:必要なパッケージの読み込み
# パッケージの読み込み
library(ggplot2)
library(dplyr)
seed <- 202507202.2 シミュレーションの実行
Step 1: パラメータの設定
# --- シミュレーションパラメータ ---
S0 <- 100 # 初期株価
mu <- 0.05 # ドリフト率(期待リターン, 5%)
sigma <- 0.2 # ボラティリティ(変動率, 20%)
T_end <- 1.0 # シミュレーション期間(1年)
N_steps <- 252 # 時間ステップ数(1年の営業日数)
dt <- T_end / N_steps # 時間ステップ幅
N_paths <- 100 # シミュレートするパス(ありうる未来)の数
# シミュレーションの条件を表示
cat("--- シミュレーション条件 ---\n\n")
cat("モデル: 幾何ブラウン運動(確率微分方程式)\n")
cat(sprintf("初期株価: %.2f\n", S0))
cat(sprintf("ドリフト率μ: %.2f, ボラティリティσ: %.2f\n", mu, sigma))
cat(sprintf("シミュレーション期間: %.1f年, パス数: %d本\n", T_end, N_paths))
cat("--------------------------\n")--- シミュレーション条件 ---
モデル: 幾何ブラウン運動(確率微分方程式)
初期株価: 100.00
ドリフト率μ: 0.05, ボラティリティσ: 0.20
シミュレーション期間: 1.0年, パス数: 100本
--------------------------Step 2: シミュレーションループの実行(オイラー・丸山法)
set.seed(seed)
# 結果を保存するためのデータフレームを準備
all_paths <- data.frame()
# パスごとにシミュレーションを実行するループ
for (i in 1:N_paths) {
# このパスの価格履歴を保存するベクトル
S <- numeric(N_steps + 1)
S[1] <- S0
# 時間発展の計算ループ
for (t in 1:N_steps) {
# 標準正規分布に従う乱数を生成
Z <- rnorm(1)
# ΔW_t を計算
dW <- Z * sqrt(dt)
# オイラー・丸山法による更新
S[t + 1] <- S[t] + mu * S[t] * dt + sigma * S[t] * dW
}
# このパスの結果をデータフレームにまとめる
path_df <- data.frame(
path_id = i,
time_step = 0:N_steps,
time = (0:N_steps) * dt,
price = S
)
# 全体の結果に追加
all_paths <- rbind(all_paths, path_df)
}Step 3: 結果の可視化
# ggplotで多数のパスをプロット
p <- ggplot(all_paths, aes(x = time, y = price, group = path_id)) +
# 多数のパスを半透明で描画
geom_line(aes(color = path_id), alpha = 0.4, show.legend = FALSE) +
# 決定論的な期待成長曲線(ノイズがない場合)を太線で追加
geom_line(
data = . %>% filter(path_id == 1), # データはどれでも良い
aes(y = S0 * exp(mu * time)),
color = "red", linewidth = 1.2, linetype = "dashed"
) +
annotate("text",
x = T_end * 0.7, y = S0 * exp(mu * T_end) * 1.1,
label = "期待成長曲線 (σ=0の場合)", color = "red"
) +
labs(
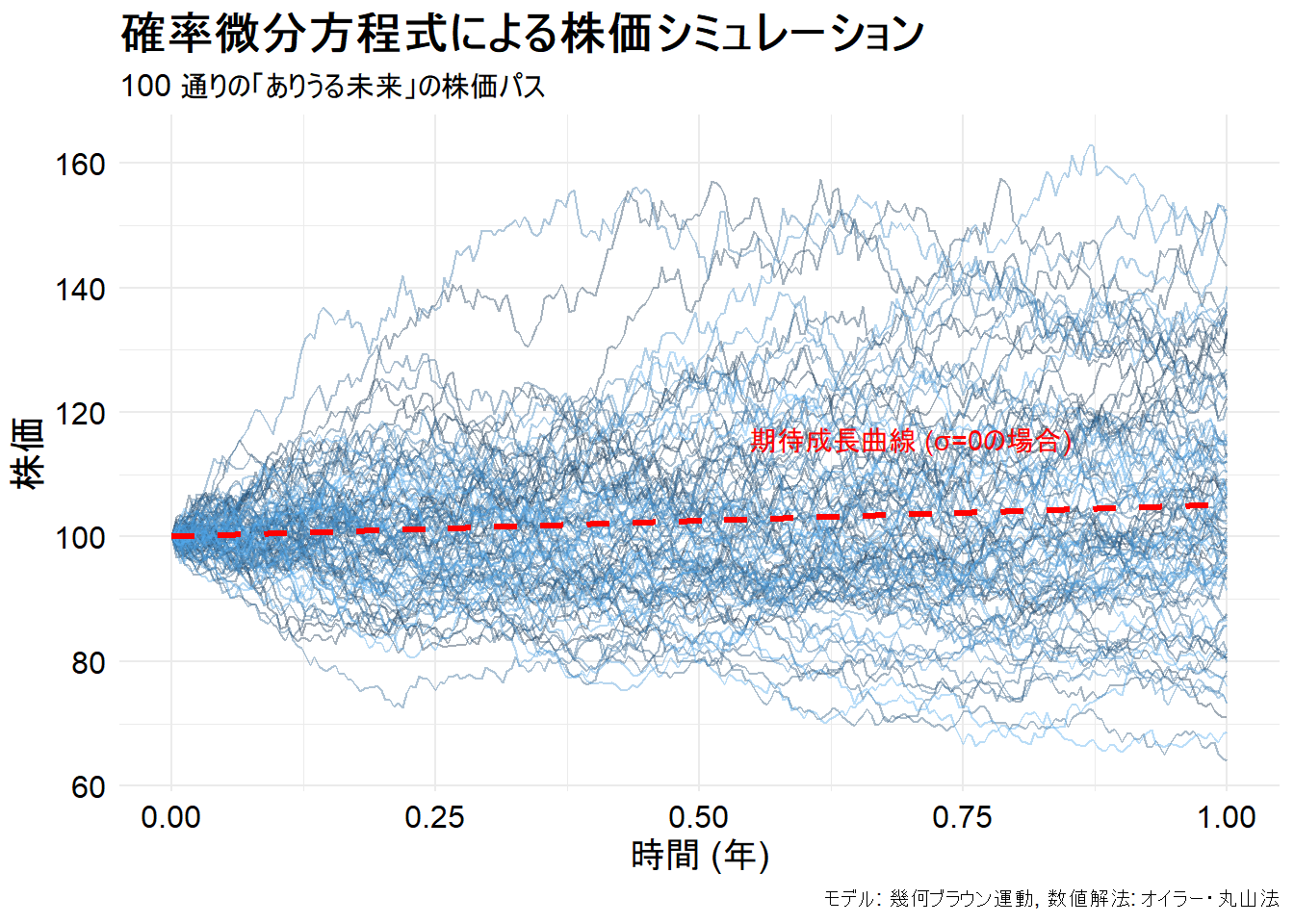
title = "確率微分方程式による株価シミュレーション",
subtitle = paste(N_paths, "通りの「ありうる未来」の株価パス"),
x = "時間 (年)",
y = "株価",
caption = "モデル: 幾何ブラウン運動, 数値解法: オイラー・丸山法"
) +
theme_minimal() +
theme(
plot.title = element_text(size = 18, face = "bold"),
plot.subtitle = element_text(size = 12),
axis.title = element_text(size = 14),
axis.text = element_text(size = 12, color = "black")
)
# グラフを表示
print(p)Figure 1 から、SDEが記述する世界の特徴がわかります。
- 多様な未来: シミュレーションを開始する条件は全て同じでも、ランダムなノイズの影響で、1年後の株価は様々な値を取り得ます。これが確率微分方程式が描く世界です。
- トレンドとばらつき: 赤い破線は、もしランダムな揺らぎがなければ(
σ=0)株価がたどるであろう平均的な成長経路(ドリフト)です。実際のパスは、このトレンドの周りで、ボラティリティσの大きさに応じてばらついています。 - 時間の経過と共に広がる不確実性: 未来に進むほど、各パスの間のばらつき(不確実性の幅)が大きくなっているのが分かります。
このように、確率微分方程式は単一の未来を予測するのではなく、考えられる無数の未来のシナリオ群を生成し、その統計的性質を分析するための枠組みを提供します。
以上です。