Rで 逆2次補間法 を試みます。
本ポストはこちらの続きです。

1. 逆2次補間法とは
逆2次補間法(Inverse Quadratic Interpolation)は、方程式 f(x) = 0 の解を求めるためのアルゴリズムです。
基本的なアイデア
- はさみうち法: 2つの点
(x0, y0)と(x1, y1)を通る直線を考え、その直線がx軸と交わる点を次の近似解としました。 - 逆2次補間法: 3つの既知の点
(x0, y0), (x1, y1), (x2, y2)を通る放物線を考え、その放物線がx軸と交わる点を次の近似解とします。
なぜ「逆」なのか?
通常の放物線 y = ax^2 + bx + c を使うのではなく、xとyの役割を入れ替えた「逆関数」x = g(y) を考えます。この逆関数 g(y) を2次の多項式(放物線)で近似します。
x = A * y^2 + B * y + C
この「逆」の形を使うことにメリットがあります。 私たちが求めたいのは f(x) = 0、すなわち y=0 となる x の値です。上記の「逆」の式に y=0 を代入すると、次の近似解 x は以下の通りに計算できます。
x = A * 0^2 + B * 0 + C
x = C
つまり、3点を通る横向きの放物線の式さえ求めてしまえば、次の近似解は定数項 C として得られるのです。
アルゴリズムの手順
- 初期設定:
- 3つの異なる初期点
x0, x1, x2を設定します。 - それぞれの関数値
y0=f(x0), y1=f(x1), y2=f(x2)を計算します。 - 許容誤差
tolと最大反復回数max_iterを決めます。
- 3つの異なる初期点
- 反復計算:
3点
(y0, x0), (y1, x1), (y2, x2)を通る逆2次式を計算します。実装上は、係数A, B, Cを求めるよりも、ラグランジュ補間の公式を使うのが一般的です。次の近似解x_newは以下の式で計算されます。x_new = (y1*y2 / ((y0-y1)*(y0-y2))) * x0 + (y0*y2 / ((y1-y0)*(y1-y2))) * x1 + (y0*y1 / ((y2-y0)*(y2-y1))) * x2収束判定を行います。
abs(f(x_new))や、前回からの変化量abs(x_new - x2)が許容誤差tolより小さければ終了します。次の反復のために、点を更新します。最も古い点
x0を捨て、x1を新しいx0に、x2を新しいx1に、そして今計算したx_newを新しいx2とします。 (x0 ← x1,x1 ← x2,x2 ← x_new)
特徴
- 長所: 収束が速い。収束次数は約1.839で、ニュートン法(次数2)に迫る速度です。
- 短所:
- 不安定さ: 単独で使うには不安定な手法です。3点の関数値
y0, y1, y2が互いに異なっている必要があります(式の分母がゼロになるため)。 - 暴走の危険: 3点が解から遠い場合、近似した放物線が実際の関数と大きく異なり、次の近似解がとんでもない場所に飛んで行ってしまうことがあります。
- 不安定さ: 単独で使うには不安定な手法です。3点の関数値
この短所のため、逆2次補間法は単独で使われることはほとんどなく、ブレント法のように、二分法などの頑健な手法と組み合わせたハイブリッドアルゴリズムの一部として利用されます。
2. R言語によるシミュレーションコードと実行結果
それでは、これまでと同じ方程式 f(x) = x^3 - x - 1 = 0 を、逆2次補間法(単独)で解くシミュレーションを行います。
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
# -----------------------------------------------------------------
# 1. シミュレーションの対象となる関数を定義 (これまでと同じ)
# -----------------------------------------------------------------
# f(x) = x^3 - x - 1
f <- function(x) {
return(x^3 - x - 1)
}
# -----------------------------------------------------------------
# 2. 逆2次補間法のシミュレーションを行う関数を定義
# -----------------------------------------------------------------
inverse_quadratic_simulation <- function(func, x0, x1, x2, tol = 1e-12, max_iter = 10) {
cat("--- 逆2次補間法シミュレーション開始 ---\n\n")
cat(sprintf("対象関数: x^3 - x - 1\n"))
cat(sprintf("初期点: x0=%.1f, x1=%.1f, x2=%.1f\n", x0, x1, x2))
cat(sprintf("許容誤差: %e\n\n", tol))
# 各ステップの結果を保存するデータフレーム
history <- data.frame(
iter = integer(),
x_new = double(),
fx_new = double()
)
# 反復計算
for (i in 1:max_iter) {
# 現在の3点での関数値を計算
y0 <- func(x0)
y1 <- func(x1)
y2 <- func(x2)
# yの値が重複すると計算できないためチェック (簡易的)
if (y0 == y1 || y0 == y2 || y1 == y2) {
stop("関数値yが重複しました。異なる関数値を持つ3点を選択してください。")
}
# ラグランジュ補間による次の近似解の計算
x_new <- (y1 * y2 / ((y0 - y1) * (y0 - y2))) * x0 +
(y0 * y2 / ((y1 - y0) * (y1 - y2))) * x1 +
(y0 * y1 / ((y2 - y0) * (y2 - y1))) * x2
fx_new <- func(x_new)
cat(sprintf("【反復 %d回目】\n", i))
cat(sprintf(" 次の近似解 x_new = %.12f\n", x_new))
cat(sprintf(" その関数値 f(x_new) = %.2e\n", fx_new))
history <- rbind(history, data.frame(
iter = i,
x_new = x_new,
fx_new = fx_new
))
# 収束判定
if (abs(fx_new) < tol || abs(x_new - x2) < tol) {
cat("\n--- 収束しました ---\n\n")
break
}
# 次の反復のために点を更新
x0 <- x1
x1 <- x2
x2 <- x_new
}
if (i == max_iter) {
cat("\n--- 最大反復回数に達しました ---\n")
}
cat(sprintf("最終的な解の近似値 = %.12f\n", x_new))
return(history)
}
# -----------------------------------------------------------------
# 3. シミュレーションの実行
# -----------------------------------------------------------------
# 3つの初期点を設定
sim_history_iqi <- inverse_quadratic_simulation(f, x0 = 2.0, x1 = 1.5, x2 = 1.0)
# -----------------------------------------------------------------
# 4. ggplot2による結果の可視化
# -----------------------------------------------------------------
# 最終的な解の値を取得
final_solution_value <- tail(sim_history_iqi, 1)$x_new
# 収束プロセスのプロット
iqi_process_plot <- ggplot(sim_history_iqi, aes(x = iter, y = x_new)) +
geom_hline(yintercept = final_solution_value, linetype = "dashed", color = "red", linewidth = 1) +
geom_text(aes(x = 0.5, y = final_solution_value, label = sprintf("真の解\n(約 %.6f)", final_solution_value)),
color = "red", hjust = 0, vjust = -0.2
) +
geom_line(color = "gray50", linewidth = 1) +
geom_point(color = "#7CAE00", size = 5, stroke = 1.5) +
labs(
title = "逆2次補間法の収束プロセス",
subtitle = "近似解がどのように真の解に収束するか (単独使用時)",
x = "反復回数 (iter)",
y = "近似解 (x_new) の値"
) +
scale_x_continuous(breaks = 1:nrow(sim_history_iqi)) +
theme_minimal(base_family = "sans")
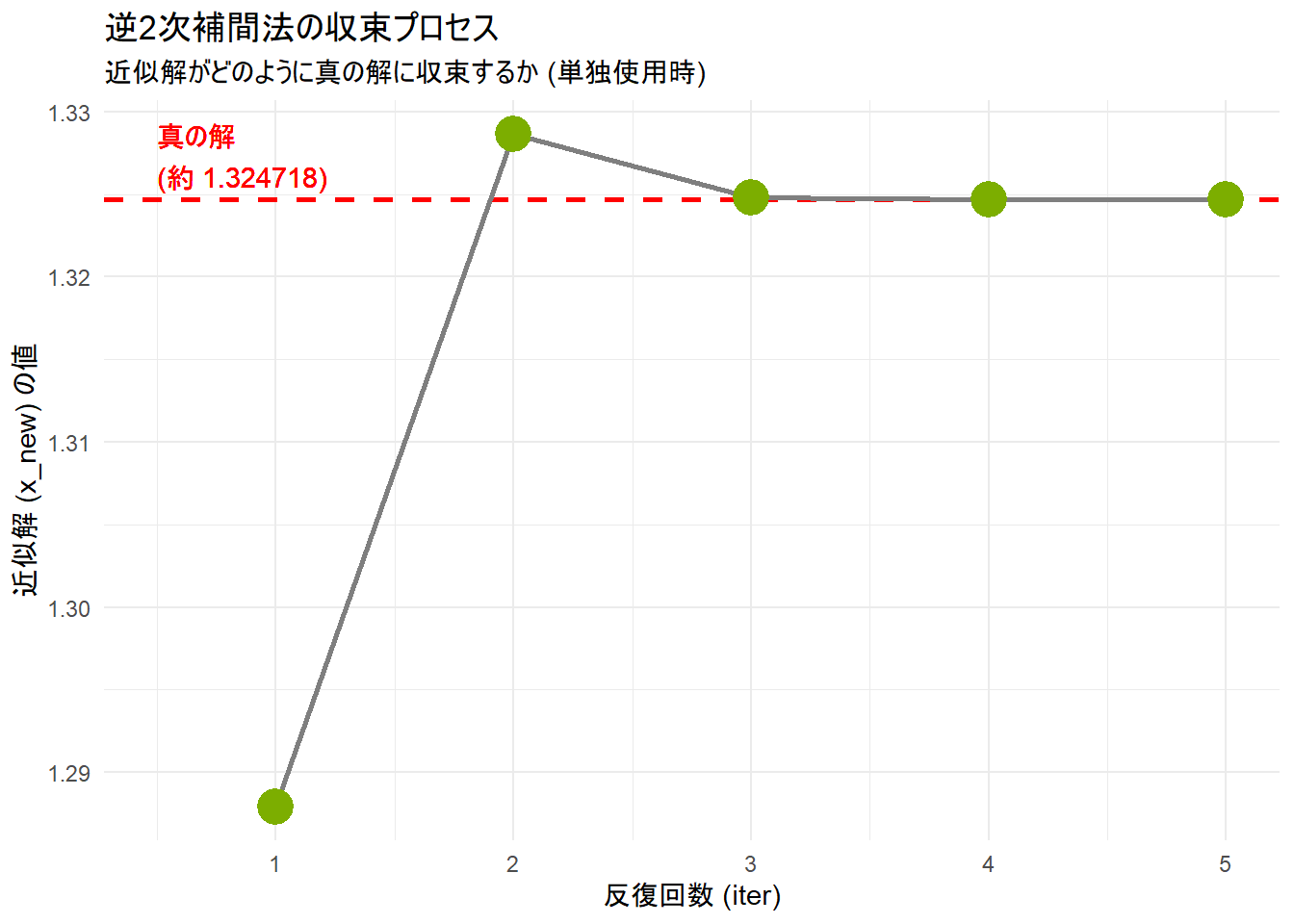
print(iqi_process_plot)--- 逆2次補間法シミュレーション開始 ---
対象関数: x^3 - x - 1
初期点: x0=2.0, x1=1.5, x2=1.0
許容誤差: 1.000000e-12
【反復 1回目】
次の近似解 x_new = 1.287878787879
その関数値 f(x_new) = -1.52e-01
【反復 2回目】
次の近似解 x_new = 1.328636327931
その関数値 f(x_new) = 1.68e-02
【反復 3回目】
次の近似解 x_new = 1.324824564675
その関数値 f(x_new) = 4.55e-04
【反復 4回目】
次の近似解 x_new = 1.324717933318
その関数値 f(x_new) = -1.02e-07
【反復 5回目】
次の近似解 x_new = 1.324717957245
その関数値 f(x_new) = -6.53e-14
--- 収束しました ---
最終的な解の近似値 = 1.324717957245注目点: 二分法は17回、はさみうち法は15回、ブレント法は10回で収束しましたが、5回の反復で、関数値
f(x_new)がほぼゼロ(計算機の表示限界)に達し、許容誤差1e-12を下回る精度の解が、今回のサンプルでは上手いこと、得られました。
グラフの読み方
- 横軸: シミュレーションの反復回数です。
- 縦軸: 各ステップで計算された近似解
x_newの値です。 - 赤い破線: この方程式の真の解(最終的な収束値)を示します。
- 緑の点と灰色の線: 各ステップで得られた近似解が、真の解に収束していく様子を示しています。
3. 収束次数の考え方
アルゴリズムの「速さ」を測る指標として収束次数 (order of convergence) p があります。これは、反復計算を1回進めるごとに、解との誤差がどれくらい小さくなるかを示します。
ステップ n での解との誤差を ε_n とすると、収束次数 p のアルゴリズムは、おおよそ以下の関係を満たします。
|ε_{n+1}| ≈ C * |ε_n|^p
ここで C は定数です。
-
p=1なら線形収束です(二分法など)。誤差が毎回一定の「割合」でしか減りません。 -
p>1なら超線形収束です。誤差が前の誤差のp乗で減っていくため、収束がどんどん加速します。 -
p=2なら2次収束です(ニュートン法)。誤差の桁数が反復ごとにほぼ倍になる、高速な収束です。
1.839 の導出過程(セカント法との比較)
逆2次補間法(3点を使う)の導出は少し複雑なので、まずはそれとよく似たセカント法(はさみうち法と同様に2点を使う)から見てみましょう。こちらの収束次数は約1.618で、これは黄金比 φ として有名です。
ステップ1:セカント法(2点使用)の場合 (p ≈ 1.618)
セカント法では、n+1 回目の誤差 ε_{n+1} は、前の2回、n 回目と n-1 回目の誤差を使って、おおよそ以下の関係になることが知られています。
|ε_{n+1}| ≈ K * |ε_n| * |ε_{n-1}| (Kは定数)
ここで、収束次数が p であると仮定すると、|ε_{n+1}| ≈ C|ε_n|^p と |ε_n| ≈ C|ε_{n-1}|^p が成り立ちます。後者の式を変形すると |ε_{n-1}| ≈ ( |ε_n| / C )^(1/p) となります。
これらを最初の式に代入すると、
C|ε_n|^p ≈ K * |ε_n| * (|ε_n| / C)^(1/p)
両辺の ε_n の指数(肩に乗っている数字)を比較すると、
p = 1 + 1/p
この方程式の両辺に p を掛けると、
p² = p + 1 → p² - p - 1 = 0
この2次方程式の正の解が、まさしく黄金比 φ = (1 + √5) / 2 ≈ 1.618… なのです。
ステップ2:逆2次補間法(3点使用)の場合 (p ≈ 1.839)
では、本題の逆2次補間法です。 この手法は、n 回目、n-1 回目、n-2 回目の3つの点を使って次の点を決めます。そのため、誤差の関係式は以下のようになります。
|ε_{n+1}| ≈ K * |ε_n| * |ε_{n-1}| * |ε_{n-2}|
先ほどと同じように、収束次数 p を仮定して ε_n, ε_{n-1}, ε_{n-2} を ε_n の式で表現し、指数を比較すると、
p = 1 + 1/p + 1/p²
この方程式の両辺に p² を掛けると、
p³ = p² + p + 1 → p³ - p² - p - 1 = 0
この3次方程式が出てきました。この方程式には実数解が1つと、複素数解が2つありますが、収束次数として意味を持つのは唯一の正の実数解です。そして、この解を数値的に計算すると、
p ≈ 1.839286755...
となります。これが「約1.839」の正体です。この値はトリボナッチ定数 (Tribonacci constant) とも呼ばれます。
まとめ
| 手法 | 使用する点の数 | 収束次数の元となる方程式 | 収束次数 (p) | 備考 |
|---|---|---|---|---|
| 二分法 | 2 (区間) | – | 1 | 線形収束 |
| セカント法 | 2 | p² - p - 1 = 0 | ≈ 1.618 | 黄金比 |
| 逆2次補間法 | 3 | p³ - p² - p - 1 = 0 | ≈ 1.839 | トリボナッチ定数 |
| ニュートン法 | 1 (+導関数) | – | 2 | 2次収束 |
このように、1.839という数値は、逆2次補間法が「3つの過去の点を使って次の点を予測する」というアルゴリズムの構造から必然的に導かれる数学的な定数です。
以上です。