Rで サンプルサイズ設計:2変数の相関分析 を確認します。
1. シミュレーションのシナリオ
シナリオ:スマートフォンの利用時間と睡眠時間の関係調査
ある大学の健康科学研究室が、大学生の心身の健康に関する調査の一環として、「スマートフォンの1日の平均利用時間」と「平日の平均睡眠時間」の関係性を明らかにしたいと考えています。
- 研究の仮説: スマートフォンの利用時間が長い学生ほど、睡眠時間が短いのではないか。つまり、2つの変数間には負の相関が存在するのではないか。
- 調査対象: 大学生
- 測定項目:
- 変数1: 1日の平均スマートフォン利用時間(スクリーンタイム機能などから客観的に測定)
- 変数2: 平日の1日の平均睡眠時間(活動量計や睡眠アプリから客観的に測定)
サンプルサイズ設計のためのパラメータ設定:
- 有意水準 (α): 慣例に従い
0.05(両側検定)に設定します。 - 検出力 (1 – β): もし中程度の相関が存在するならば、それを見逃さないように80%の確率で検出したいので、
0.80に設定します。 - 効果量 (r):
- 先行研究や予備調査に基づき、スマートフォン利用時間と睡眠時間の間には中程度の負の相関 (r = -0.3) があると予測しました。この程度の相関が確認できれば、学生への健康指導に活かす価値があると判断します。
- サンプルサイズ計算で用いる効果量は相関係数の絶対値なので、r = 0.3 とします。
このシナリオに基づき、「-0.3程度の相関を80%の確率で検出するには、何人の学生を調査する必要があるか?」を計算し、シミュレーションで検証します。
各パラメータの意味
- 有意水準 (α, alpha)
- 帰無仮説(H₀: 母集団の相関係数ρは0である)が棄却されないにもかかわらず、それを棄却してしまう確率(第1種の過誤)。
- 一般的に
α = 0.05に設定されますが、目的により異なります。
- 検出力 (Power, 1 – β)
- 対立仮説(H₁: 母集団の相関係数ρは0ではない)が真であるときに、その相関を正しく検出できる確率。
βは第2種の過誤(相関があることを見逃す確率)です。 - 一般的に
1 - β = 0.80や0.90に設定されますが、目的により異なります。
- 対立仮説(H₁: 母集団の相関係数ρは0ではない)が真であるときに、その相関を正しく検出できる確率。
- 効果量 (Effect Size)
- 相関係数の検定における効果量は、検出したい相関係数 (r) そのものです。値は-1から+1の範囲を取ります。
- Cohen(1988)による効果量の目安: r = 0.1 (小), r = 0.3 (中), r = 0.5 (大)
- 研究分野の先行研究や、意味のある関連性の強さに基づいて設定します。
- サンプルサイズ (n)
- 研究に必要なペアの数(観測数)。これを求めます。
相関分析における効果量
「検出したいと考える相関係数の値そのもの」が効果量として直接的に用いられます。
効果量(Effect Size)の定義は、「関心のある現象が、どの程度の大きさで母集団に存在しているかを示す指標」であり、効果量は「標準化(単位に依存しない)」された指標です。
他の検定と比較しますと以下のとおりです。
- t検定の場合 (Cohen’s d):
d = (μ₁ - μ₂) / σ- 2群の平均値の差
μ₁ - μ₂は、元のデータの単位(点、cm, kgなど)に依存します。 - これを共通の標準偏差
σで割ることで、単位に依存しない標準化された差になります。これが効果量です。
- 相関係数の検定の場合 (Pearson’s r):
- 相関係数
rは、その定義からすでに -1から+1の範囲に標準化された値です。 - r = Cov(x, y) / (σ_x * σ_y) という計算式自体に、標準偏差で割る操作が含まれています。
- したがって、相関係数
rはそれ自体が「2つの変数の関連性の強さ」を示す、単位に依存しない標準化された指標です。
- 相関係数
このため、t検定のように別途「効果量d」を計算する必要がなく、検出したい相関係数rの値そのものを効果量として、サンプルサイズ設計の計算に直接利用し、2つの連続変数間の直線的な関連の強さと向きを示すピアソンの積率相関係数 (ρ) について、その値が0と有意に異なるか(つまり、無相関ではないか)を検定します。
フィッシャーのz変換
標本相関係数rの分布は正規分布ではないため、フィッシャーのz変換 (Fisher’s z-transformation) を用いて、rを正規分布に近似する変数zに変換します。
z = 0.5 * log((1 + r) / (1 – r))
この変換後のzは、平均 0.5 * log((1 + ρ) / (1 - ρ))、標準偏差 1 / sqrt(n - 3) の正規分布に近似的に従います。この性質を利用して、設定したα、1-β、rを満たすために必要なサンプルサイズ n を計算することができます。
2. R言語によるシミュレーションコード
まず、必要なライブラリを読み込みます。
library(pwr)
library(ggplot2)
library(dplyr)
library(MASS) # 多変量正規分布のデータを生成するために使用
seed <- 20250709ステップ1: シナリオに基づいたサンプルサイズの計算
Rのpwrパッケージにあるpwr.r.test関数を使用します。
cat("--- ステップ1: サンプルサイズの計算 ---\n")
# パラメータ設定
effect_size_r <- 0.3 # 検出したい相関係数r
sig_level <- 0.05 # 有意水準 alpha
power_level <- 0.80 # 検出力 1-beta
# サンプルサイズの計算
# nをNULLにすることで、必要なサンプルサイズを計算させる
sample_size_calc <- pwr.r.test(
r = effect_size_r,
sig.level = sig_level,
power = power_level,
alternative = "two.sided" # 両側検定
)
# 結果の表示
print(sample_size_calc)
# 必要なサンプルサイズ(学生の数)を取得(切り上げ)
n_required <- ceiling(sample_size_calc$n)
cat("\n")
cat(paste0("結論: この調査には最低 ", n_required, " 人の学生が必要です。\n"))--- ステップ1: サンプルサイズの計算 ---
approximate correlation power calculation (arctangh transformation)
n = 84.07364
r = 0.3
sig.level = 0.05
power = 0.8
alternative = two.sided
結論: この調査には最低 85 人の学生が必要です。計算結果から、この調査には85人の学生が必要であることがわかります。
ステップ2: 検出力のシミュレーション (対立仮説が真の場合)
計算で得られたサンプルサイズ(85人)を用いて、本当に検出力が80%程度になるかシミュレーションで確認します。
cat("--- ステップ2: 検出力のシミュレーション ---\n")
# シミュレーションのパラメータ設定
set.seed(seed) # 結果を再現可能にする
n_sim <- 10000 # シミュレーション回数
# シナリオの母集団パラメータ
# 平均ベクトル(スマホ利用時間6時間、睡眠時間7時間と仮定)
mu_vector <- c(6, 7)
# 標準偏差(スマホ2時間、睡眠1時間と仮定)
sd_vector <- c(2, 1)
# 相関係数
rho <- -0.3 # 負の相関を想定
# 共分散行列を作成
sigma_matrix <- matrix(
c(
sd_vector[1]^2, rho * sd_vector[1] * sd_vector[2],
rho * sd_vector[1] * sd_vector[2], sd_vector[2]^2
),
nrow = 2
)
# 結果を格納するベクトル
p_values_h1 <- numeric(n_sim)
# シミュレーションループ
for (i in 1:n_sim) {
# 1. 対立仮説が真である状況の相関のあるデータを生成
correlated_data <- mvrnorm(n = n_required, mu = mu_vector, Sigma = sigma_matrix)
# 2. 相関係数の検定を実行
cor_test_result <- cor.test(correlated_data[, 1], correlated_data[, 2])
# 3. p値を保存
p_values_h1[i] <- cor_test_result$p.value
}
# シミュレーションによる検出力の計算
simulated_power <- mean(p_values_h1 < sig_level)
cat(paste0("\nシミュレーションによる検出力: ", round(simulated_power, 3), "\n"))--- ステップ2: 検出力のシミュレーション ---
シミュレーションによる検出力: 0.806シミュレーション結果は、目標とした検出力0.80に近い値(約0.806)となり、サンプルサイズ設計の妥当性が裏付けられました。
ステップ3: 検出力シミュレーション結果の可視化
cat("--- ステップ3: 検出力シミュレーション結果の可視化 ---\n")
p_values_df_h1 <- data.frame(p_value = p_values_h1)
plot_power <- ggplot(p_values_df_h1, aes(x = p_value)) +
geom_histogram(binwidth = 0.05, fill = "skyblue", color = "black", boundary = 0) +
geom_vline(xintercept = sig_level, color = "red", linetype = "dashed", linewidth = 1) +
annotate("text",
x = 0.5, y = 4500,
label = paste("シミュレーションによる検出力 (p < 0.05) =", round(simulated_power, 3)),
color = "red", size = 5
) +
labs(
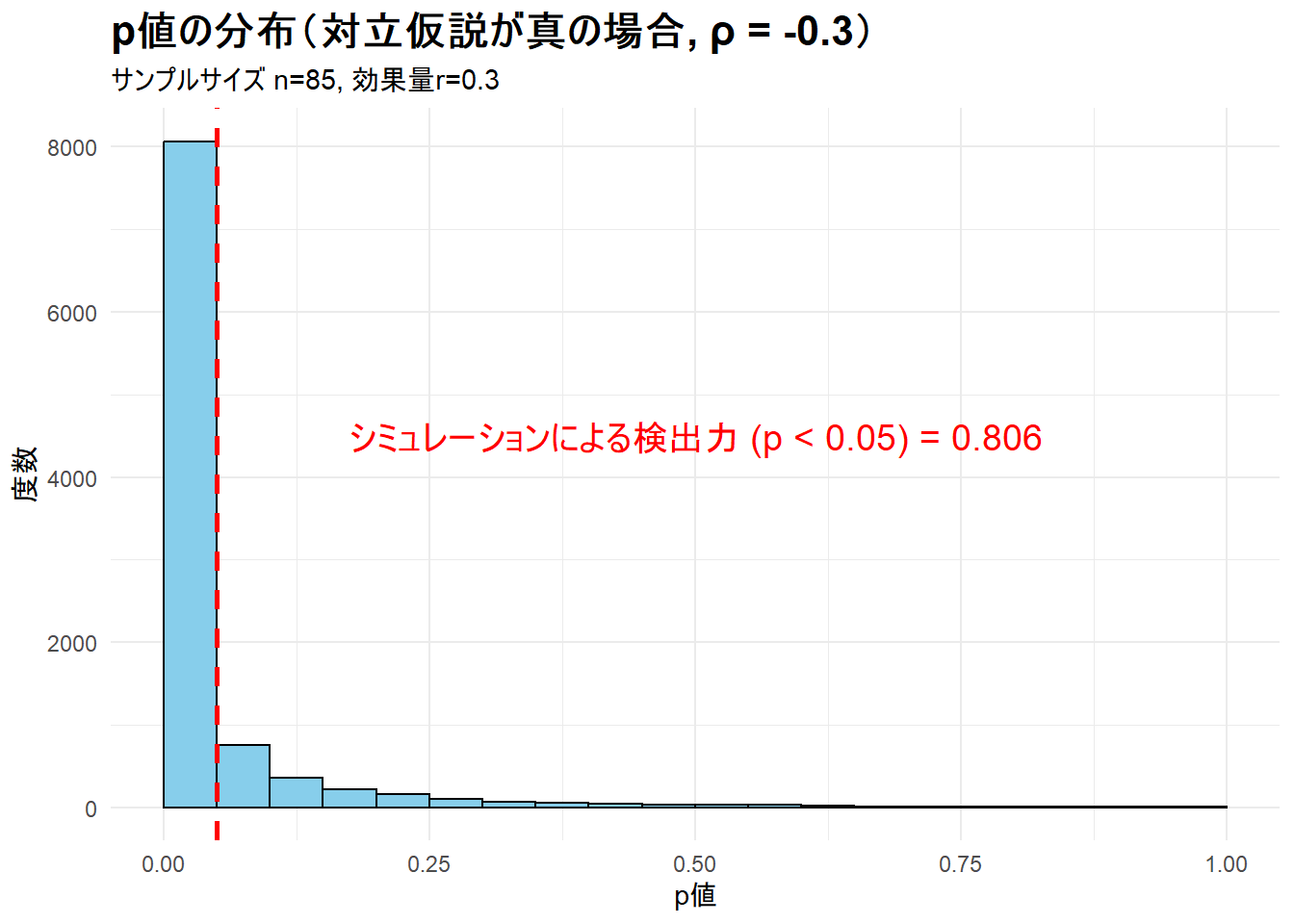
title = "p値の分布(対立仮説が真の場合, ρ = -0.3)",
subtitle = paste0("サンプルサイズ n=", n_required, ", 効果量r=", effect_size_r),
x = "p値",
y = "度数"
) +
theme_minimal() +
theme(plot.title = element_text(size = 16, face = "bold"))
print(plot_power)--- ステップ3: 検出力シミュレーション結果の可視化 ---Figure 1 から p値が0に近い方に偏っており、0.05(赤い破線)よりも左側に分布する割合(=検出力)が全体の約80%を占めていることを確認できます。
ステップ4: 第1種の過誤のシミュレーション (帰無仮説が棄却されない場合)
次に、2つの変数に全く相関がない場合(帰無仮説 ρ=0 が棄却されない場合)に、誤って「相関あり」と結論づけてしまう確率(第1種の過誤率)が、設定した有意水準α (0.05)と一致するかを確認します。
cat("--- ステップ4: 第1種の過誤のシミュレーション ---\n")
# 帰無仮説が棄却されない場合 (相関係数 rho = 0)
rho_h0 <- 0
sigma_matrix_h0 <- matrix(
c(
sd_vector[1]^2, rho_h0 * sd_vector[1] * sd_vector[2],
rho_h0 * sd_vector[1] * sd_vector[2], sd_vector[2]^2
),
nrow = 2
)
p_values_h0 <- numeric(n_sim)
for (i in 1:n_sim) {
# 1. 帰無仮説が棄却されない状況の無相関のデータを生成
uncorrelated_data <- mvrnorm(n = n_required, mu = mu_vector, Sigma = sigma_matrix_h0)
# 2. 相関係数の検定を実行
cor_test_result_h0 <- cor.test(uncorrelated_data[, 1], uncorrelated_data[, 2])
# 3. p値を保存
p_values_h0[i] <- cor_test_result_h0$p.value
}
type1_error_rate <- mean(p_values_h0 < sig_level)
cat(paste("\nシミュレーションによる第1種の過誤率:", round(type1_error_rate, 3), "\n"))--- ステップ4: 第1種の過誤のシミュレーション ---
シミュレーションによる第1種の過誤率: 0.053 シミュレーションによる第1種の過誤率は、設定した有意水準0.05に近い値(約0.053)となり、検定が正しく機能していることがわかります。
ステップ5: 第1種の過誤シミュレーション結果の可視化
cat("--- ステップ5: 第1種の過誤シミュレーション結果の可視化 ---\n")
p_values_df_h0 <- data.frame(p_value = p_values_h0)
expected_freq <- n_sim * 0.05
plot_alpha <- ggplot(p_values_df_h0, aes(x = p_value)) +
geom_histogram(binwidth = 0.05, fill = "lightcoral", color = "black", boundary = 0) +
geom_vline(xintercept = sig_level, color = "blue", linetype = "dashed", linewidth = 1) +
geom_hline(yintercept = expected_freq, color = "darkgreen", linetype = "dotted", linewidth = 1) +
annotate("text",
x = 0.5, y = 600,
label = paste("第1種の過誤の確率 (p < 0.05) =", round(type1_error_rate, 3)),
color = "blue", size = 5
) +
labs(
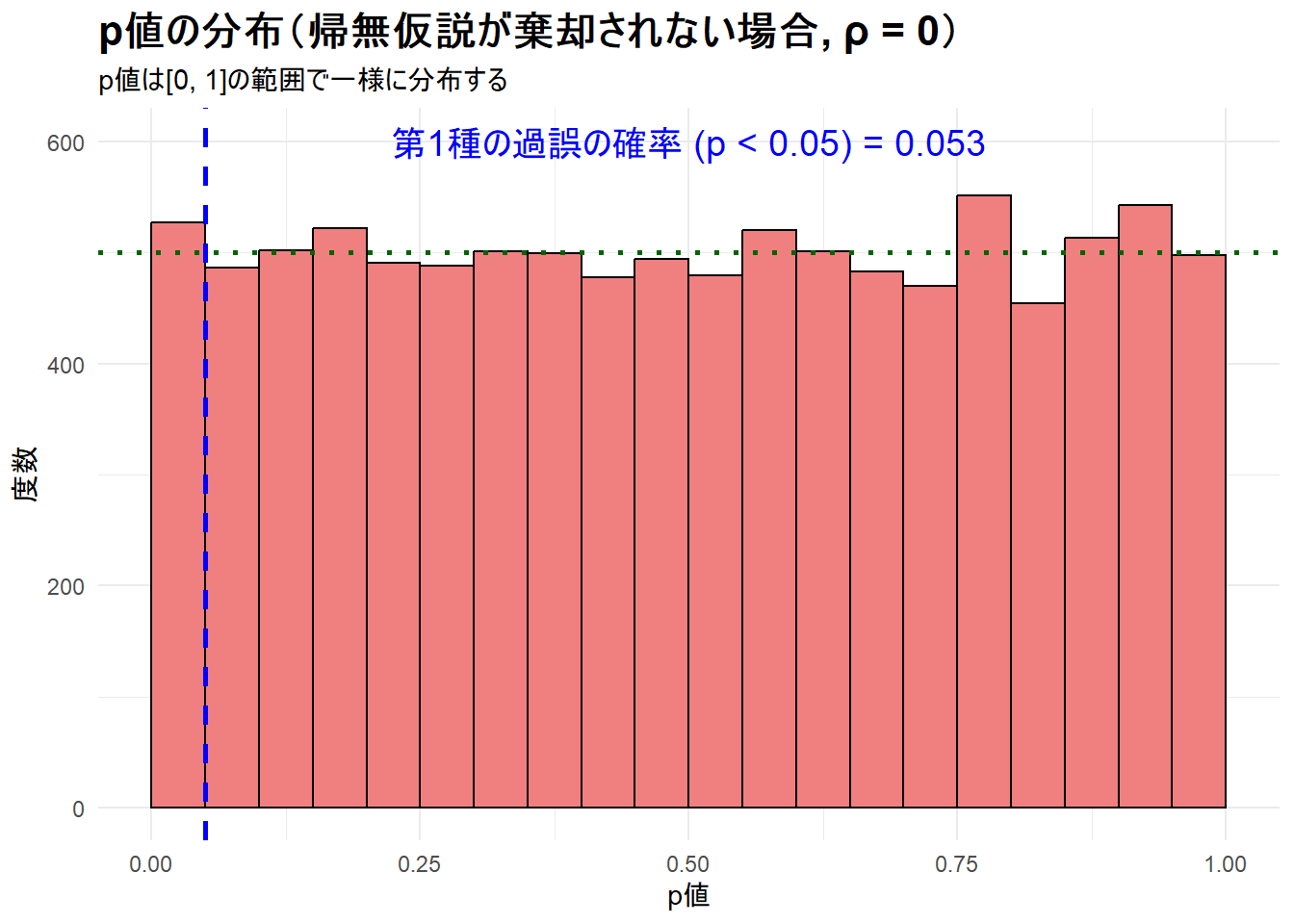
title = "p値の分布(帰無仮説が棄却されない場合, ρ = 0)",
subtitle = "p値は[0, 1]の範囲で一様に分布する",
x = "p値",
y = "度数"
) +
theme_minimal() +
theme(plot.title = element_text(size = 16, face = "bold"))
print(plot_alpha)--- ステップ5: 第1種の過誤シミュレーション結果の可視化 ---Figure 2 は、p値がほぼフラットな分布を示しており、これにより、偶然だけで有意な相関が検出されてしまう確率が、意図通り5%にコントロールされていることが視覚的に確認できます。
以上です。