Rでシンプソンのパラドックス

Rで シンプソンのパラドックス を試みます。

1. シンプソンのパラドックスとは

シンプソンのパラドックスとは、「複数のグループに分けてデータを分析した結果と、それらをまとめて（集計して）分析した結果が、正反対になる」という統計学上の現象です。

この逆転現象は、データに影響を与える「潜在変数（Lurking Variable）」や「交絡変数（Confounding Variable）」と呼ばれる、隠れた要因を見落とすことで発生します。全体で見たときの相関関係が、実際にはこれらの潜在変数によって作り出された「見せかけの相関」である可能性があります。

具体例：2つの治療法の効果測定

ある病気に対する2つの治療法（治療A、治療B）の効果を比較する例を考えてみましょう。

【全体のデータ】

まず、全体のデータを見てみます。100人ずつの患者に各治療を行ったところ、治療Bの方が成功率が高いという結果になりました。

治療法	成功者数	患者総数	成功率
治療A	35人	100人	35%
治療B	75人	100人	75%

この結果だけを見ると、「治療Bの方が圧倒的に優れた治療法だ」と結論付けてしまいそうです。

【データをグループ分けして見る】

しかし、ここで患者の状態に「軽症」と「重症」という違いがあったことが分かりました。この「症状の重さ」という潜在変数でデータをグループ分けして、分析し直してみましょう。

軽症患者のデータ

治療法	成功者数	患者総数	成功率
治療A	19人	20人	95%
治療B	72人	80人	90%

軽症患者のグループでは、治療Aの方が成功率が高いことが分かります。

重症患者のデータ

治療法	成功者数	患者総数	成功率
治療A	16人	80人	20%
治療B	3人	20人	15%

重症患者のグループでも、治療Aの方が成功率が高いという結果になりました。

【結果の逆転】

結果を整理すると、以下のようになります。

軽症グループ: 治療A (95%) > 治療B (90%)
重症グループ: 治療A (20%) > 治療B (15%)
全体の合計: 治療A (35%) < 治療B (75%)

つまり、「軽症」、「重症」のどちらのグループにおいても治療Aの方が効果的なのに、全体を合計すると治療Bの方が効果的に見えてしまうのです。これがシンプソンのパラドックスです。

なぜこの現象が起きたのか？

この例では、治療法の選択に患者の「症状の重さ」という潜在変数が強く影響しています。

治療A: 主に重症患者（80人）に適用されていた。
治療B: 主に軽症患者（80人）に適用されていた。

重症患者はもともと成功率が低いため、治療Aのグループには成功率が低い患者が大多数を占めることになり、全体の成功率が35%まで押し下げられました。逆に、治療Bのグループはもともと成功率が高い軽症患者が大多数だったため、全体の成功率が75%まで大きく底上げされたのです。

このように、データを正しく理解するためには、集計された結果だけでなく、データを適切なグループに分けて分析することが非常に重要です。

2. R言語によるシミュレーション

次に、このパラドックスをR言語でシミュレーションしてみましょう。ここでは、散布図上で「全体で見ると負の相関があるように見えるが、グループ別に見ると正の相関がある」というデータセットを人工的に作成し、可視化します。

シミュレーションコード

# パッケージの読み込み
library(ggplot2)

# 再現性のための乱数シードを設定
seed <- 20250729
set.seed(seed)

# --- ステップ1: データの生成 ---

# グループAのデータを生成 (右肩上がりの相関を持つ)
# xは平均40、yはxに比例しつつ平均80あたりに分布
n_A <- 100
x_A <- rnorm(n_A, mean = 40, sd = 10)
y_A <- 1.5 * x_A + rnorm(n_A, mean = 20, sd = 15)

# グループBのデータを生成 (こちらも右肩上がりの相関を持つ)
# xは平均60、yはxに比例しつつ平均40あたりに分布
n_B <- 100
x_B <- rnorm(n_B, mean = 60, sd = 10)
y_B <- 1.5 * x_B + rnorm(n_B, mean = -50, sd = 15)

# データを1つのデータフレームに結合
sim_data <- data.frame(
  x = c(x_A, x_B),
  y = c(y_A, y_B),
  group = factor(c(rep("Group A", n_A), rep("Group B", n_B)))
)

# --- ステップ2: 全体の相関関係の分析（パラドックスの側面）---

# 全体データに対して線形回帰モデルをあてはめる
overall_model <- lm(y ~ x, data = sim_data)
cat("--- 全体データの回帰分析結果 ---\n")
# Coefficientsのxの係数（傾き）に注目
print(summary(overall_model))

# --- ステップ3: グループ別の相関関係の分析（真実の側面）---

# グループAのデータに対して線形回帰モデルをあてはめる
group_A_model <- lm(y ~ x, data = subset(sim_data, group == "Group A"))
cat("\n--- グループAの回帰分析結果 ---\n")
print(summary(group_A_model))

# グループBのデータに対して線形回帰モデルをあてはめる
group_B_model <- lm(y ~ x, data = subset(sim_data, group == "Group B"))
cat("\n--- グループBの回帰分析結果 ---\n")
print(summary(group_B_model))


# --- ステップ4: 可視化による確認 ---

# ggplot2を使ってプロットを作成
p <- ggplot(sim_data, aes(x = x, y = y)) +
  # グループごとに色分けした散布図
  geom_point(aes(color = group), alpha = 0.7, size = 3) +

  # 全体データの回帰直線（黒い実線）
  # この線は右肩下がりになる
  geom_smooth(method = "lm", se = FALSE, color = "black", formula = y ~ x, size = 1.2) +

  # グループごとの回帰直線（グループと同じ色）
  # これらの線は右肩上がりになる
  geom_smooth(aes(color = group), method = "lm", se = FALSE, formula = y ~ x, linetype = "dashed") +

  # グラフのタイトルとラベルを設定
  labs(
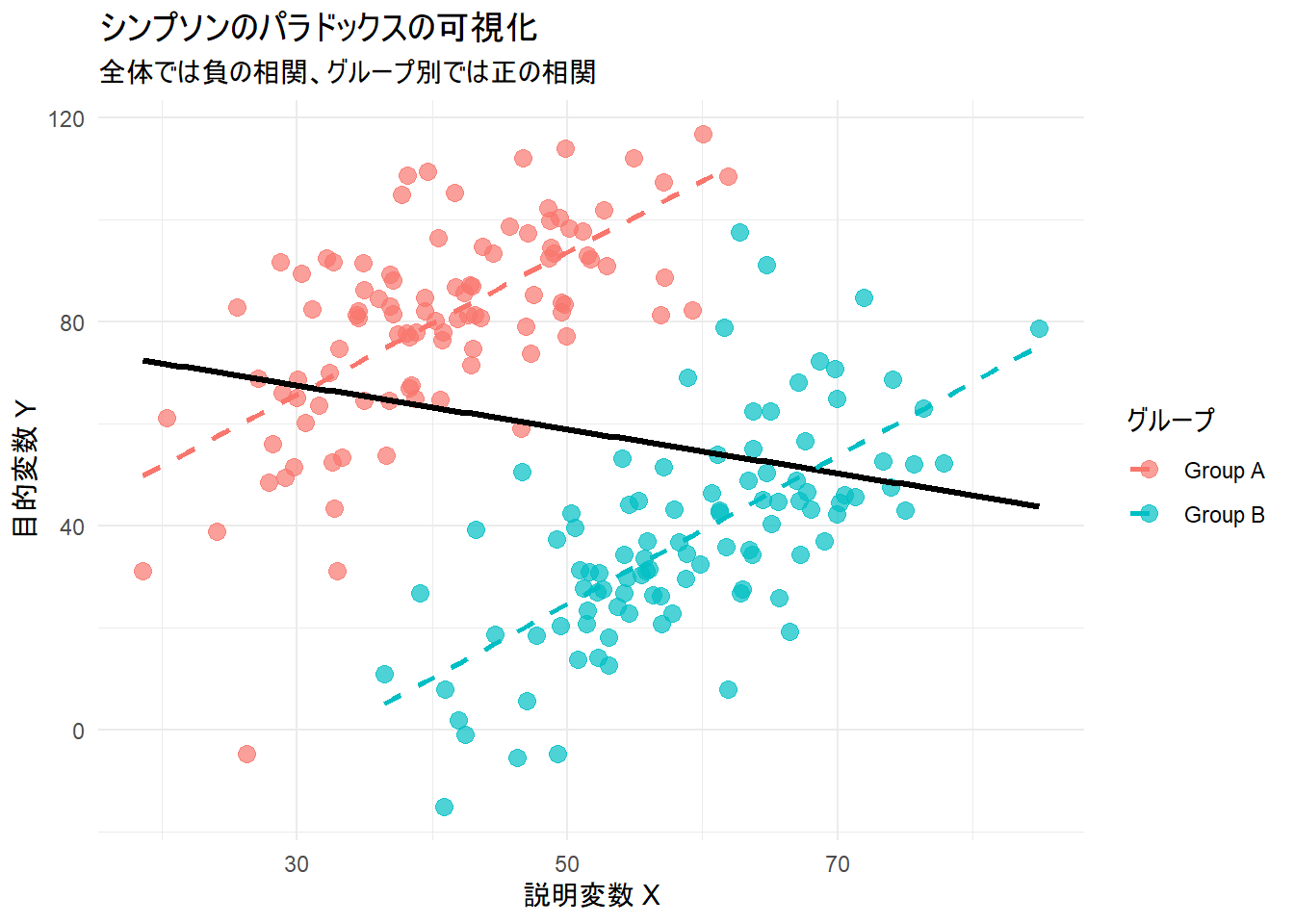
    title = "シンプソンのパラドックスの可視化",
    subtitle = "全体では負の相関、グループ別では正の相関",
    x = "説明変数 X",
    y = "目的変数 Y",
    color = "グループ"
  ) +
  theme_minimal()

# グラフを表示
print(p)

--- 全体データの回帰分析結果 ---

Call:
lm(formula = y ~ x, data = sim_data)

Residuals:
    Min      1Q  Median      3Q     Max 
-78.083 -22.006  -0.157  21.610  62.139 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  80.5257     7.9374  10.145  < 2e-16 ***
x            -0.4314     0.1542  -2.798  0.00565 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.83 on 198 degrees of freedom
Multiple R-squared:  0.03803,   Adjusted R-squared:  0.03317 
F-statistic: 7.827 on 1 and 198 DF,  p-value: 0.005655


--- グループAの回帰分析結果 ---

Call:
lm(formula = y ~ x, data = subset(sim_data, group == "Group A"))

Residuals:
    Min      1Q  Median      3Q     Max 
-65.305  -9.977   1.071   8.890  31.555 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  23.9374     7.0453   3.398 0.000984 ***
x             1.3941     0.1704   8.183 1.03e-12 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 15.43 on 98 degrees of freedom
Multiple R-squared:  0.4059,    Adjusted R-squared:  0.3998 
F-statistic: 66.96 on 1 and 98 DF,  p-value: 1.032e-12


--- グループBの回帰分析結果 ---

Call:
lm(formula = y ~ x, data = subset(sim_data, group == "Group B"))

Residuals:
    Min      1Q  Median      3Q     Max 
-34.053  -9.756  -2.219   6.511  54.281 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -47.7772     9.7233  -4.914 3.58e-06 ***
x             1.4493     0.1623   8.930 2.54e-14 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 15.48 on 98 degrees of freedom
Multiple R-squared:  0.4486,    Adjusted R-squared:  0.443 
F-statistic: 79.74 on 1 and 98 DF,  p-value: 2.541e-14

コードの解説と結果の解釈

データの生成:
- Group AとGroup Bという2つのデータ群を生成します。
- どちらのグループも、yは1.5 * xという関係を基本としているため、本来は強い正の相関（右肩上がり）を持っています。
- ただし、Group Aは(x, y)が(40, 80)あたりに、Group Bは(60, 40)あたりに分布するように平均値を調整しています。groupが潜在変数です。
全体の分析:
- lm(y ~ x, data = sim_data)で全体データに対する回帰直線の傾きを計算します。
- 出力されるCoefficients:のxの行を見ると、Estimate（係数）が負の値（-0.4314）になっています。これは「xが増えるとyが減る」という負の相関を示唆しています。
グループ別の分析:
- subset()でデータをグループに分け、それぞれの回帰直線の傾きを計算します。
- Group A、Group Bどちらのモデルでも、xの係数が正の値（1.5に近い値）になっています。これは「xが増えるとyが増える」という正の相関を示しており、こちらがデータの真の姿です。
可視化:
- 生成されたグラフを見ると、一目瞭然です。
- 黒い実線（全体）は、右肩下がりの負の相関を示しています。
- しかし、色分けされた点（グループ）は2つの塊に分かれており、それぞれの塊の中では破線（グループごと）が示すように、明確な右肩上がりの正の相関が見られます。