Rで パネル単位根検定 を試みます。
1. パネル単位根検定とは
パネルデータ(複数の個体(企業、国など)を時系列で追いかけたデータ)において、各系列が単位根(unit root)を持つかどうかを検定する手法です。
なぜ単位根検定が重要か?
時系列データが単位根を持つ(非定常である)場合、そのデータを使って回帰分析を行うと「見せかけの回帰」という問題が発生する可能性があります。これは、実際には何の関係もない変数同士の間に、統計的に有意な関係があるように見えてしまう現象です。パネルデータ分析を行う前処理として、変数が定常過程に従うか(単位根を持たないか)を確認することは非常に重要です。
パネル単位根検定は、個別の時系列データに対して単位根検定(ADF検定など)を繰り返すよりも、パネル全体の情報を利用するため、検定力が高くなるという利点があります。
LLC検定 (Levin-Lin-Chu検定)
LLC検定は、全ての個体(パネル内の各系列)で共通の自己回帰係数が存在すると仮定します。
- 帰無仮説 (\(H_0\)): 全ての系列が単位根を持つ。
- \(H_0: \rho_i = 1 \quad (\text{for all } i)\)
- 対立仮説 (\(H_A\)): 全ての系列が共通の自己回帰係数を持つ定常過程である。
- \(H_A: \rho_i = \rho < 1 \quad (\text{for all } i)\)
この検定は、パネル内の個体に強い同質性を仮定しているため、その仮定が満たされる場合には有用な検定となります。
IPS検定 (Im-Pesaran-Shin検定)
IPS検定は、LLC検定の仮定を緩め、個体ごとに異なる自己回帰係数を持つことを許容します。
- 帰無仮説 (\(H_0\)): 全ての系列が単位根を持つ。
- \(H_0: \rho_i = 1 \quad (\text{for all } i)\)
- 対立仮説 (\(H_A\)): 少なくとも一部の系列が定常過程である。
- \(H_A: \rho_i < 1 \quad (\text{for some } i)\)
IPS検定は、各系列に対して個別にADF検定を行い、それらの検定統計量(t値)を平均して検定統計量を算出します。個体間の異質性を許容するため、より現実的な状況に適用しやすい検定です。
| 検定名 | 自己回帰係数の仮定 | 対立仮説 | 特徴 |
|---|---|---|---|
| LLC検定 | 共通 (\(\rho_i = \rho\)) | 全ての系列が定常 | パネル内の同質性を仮定。検定力が高い。 |
| IPS検定 | 個別 (\(\rho_i\)) | 一部の系列が定常 | パネル内の異質性を許容。より柔軟。 |
時系列データを用いた単位根検定の検出力はあまり高くないことが知られているが, その問題をクロスセクションのサンプルを集めたパネルデータを使うことによって克服しようという考えがこれらの研究の根底にある https://hermes-ir.lib.hit-u.ac.jp/hermes/ir/re/20197/keizaikenkyu05902126.pdf
パネル単位根検定は元来パネルデータを推定する際にデータの定常性を検定するための方法として開発されたが,近年ではマクロ経済変数の収束度を計測するための分析手法としても用いられている https://dl.ndl.go.jp/view/download/digidepo_3505580_po_V45-1_02.pdf?contentNo=1&alternativeNo=
2. Rによるシミュレーション
それでは、Rを使って3つのケースでシミュレーションを行い、LLC検定とIPS検定の挙動を確認します。
- ケース1: 全ての系列が単位根を持つデータ
- ケース2: 全ての系列が定常であるデータ
- ケース3: 単位根を持つ系列と定常な系列が混在するデータ
なお、有意水準は5%とします。
準備:ライブラリのロード
まず、必要なライブラリをロードします。
# ライブラリのロード
library(plm)
library(ggplot2)
library(dplyr)
library(tidyr)シミュレーションの基本設定
seed <- 20250703
# パラメータ設定
N <- 20 # 個体数 (number of individuals)
T <- 200 # 時系列の長さ (time periods)ケース1: 全ての系列が単位根を持つ場合
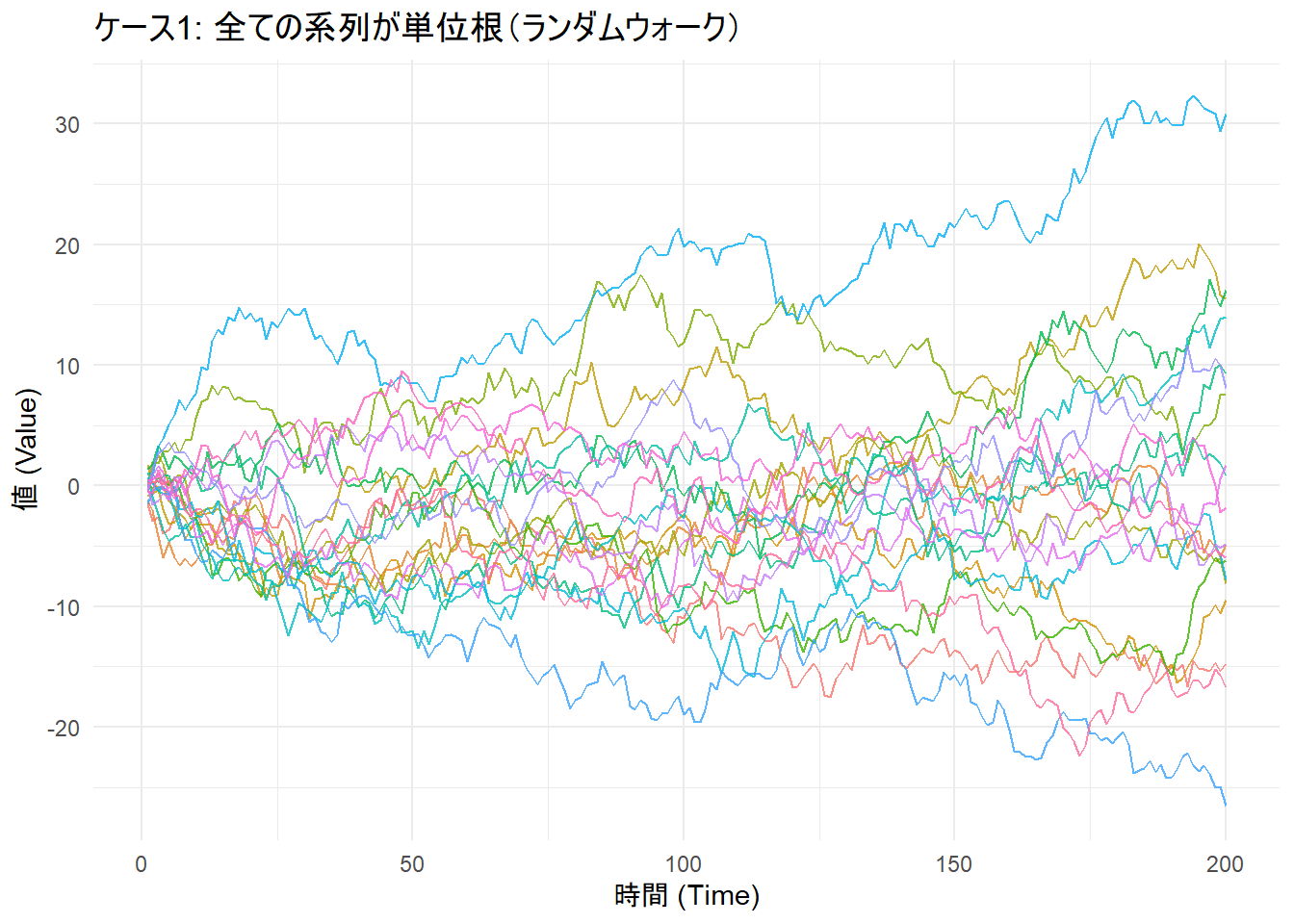
全ての系列がランダムウォーク(\(y_t = y_{t-1} + \epsilon_t\))に従うデータを生成します。この場合、帰無仮説が真であるため、検定は棄却されないはずです。
データ生成と可視化
set.seed(seed)
# データ生成
# T x N の行列を作成
y_rw <- matrix(0, nrow = T, ncol = N)
# 初期値
y_rw[1, ] <- rnorm(N, mean = 0, sd = 1)
# ランダムウォークを生成
for (t in 2:T) {
# 前期の値に正規乱数を加える
y_rw[t, ] <- y_rw[t - 1, ] + rnorm(N, mean = 0, sd = 1)
}
# データをggplotで扱いやすいロング形式に変換
panel_data_rw <- as.data.frame(y_rw) %>%
mutate(time = 1:T) %>%
pivot_longer(cols = -time, names_to = "id", values_to = "value")
# プロット
ggplot(panel_data_rw, aes(x = time, y = value, group = id, color = id)) +
geom_line(alpha = 0.8, show.legend = FALSE) +
labs(
title = "ケース1: 全ての系列が単位根(ランダムウォーク)",
x = "時間 (Time)", y = "値 (Value)"
) +
theme_minimal()パネル単位根検定の実行
plmパッケージのpurtest関数を使用します。
# パネルデータフレームに変換
pdata_rw <- pdata.frame(panel_data_rw, index = c("id", "time"))
# LLC検定
llc_test_rw <- purtest(value ~ 1, data = pdata_rw, test = "levinlin")
cat("--- LLC検定の結果 ---\n")
print(llc_test_rw)
# IPS検定
ips_test_rw <- purtest(value ~ 1, data = pdata_rw, test = "ips")
cat("--- IPS検定の結果 ---\n")
print(ips_test_rw)--- LLC検定の結果 ---
Levin-Lin-Chu Unit-Root Test (ex. var.: Individual Intercepts)
data: value ~ 1
z = -0.16418, p-value = 0.4348
alternative hypothesis: stationarity
--- IPS検定の結果 ---
Im-Pesaran-Shin Unit-Root Test (ex. var.: Individual Intercepts)
data: value ~ 1
Wtbar = -0.89098, p-value = 0.1865
alternative hypothesis: stationarity考察: LLC検定のp値は0.4348、IPS検定のp値は0.1865となりました。どちらも設定した有意水準で帰無仮説「全ての系列が単位根を持つ」を棄却できません。これは、生成したデータが実際に単位根を持つため、正しい結果と言えます。
ケース2: 全ての系列が定常である場合
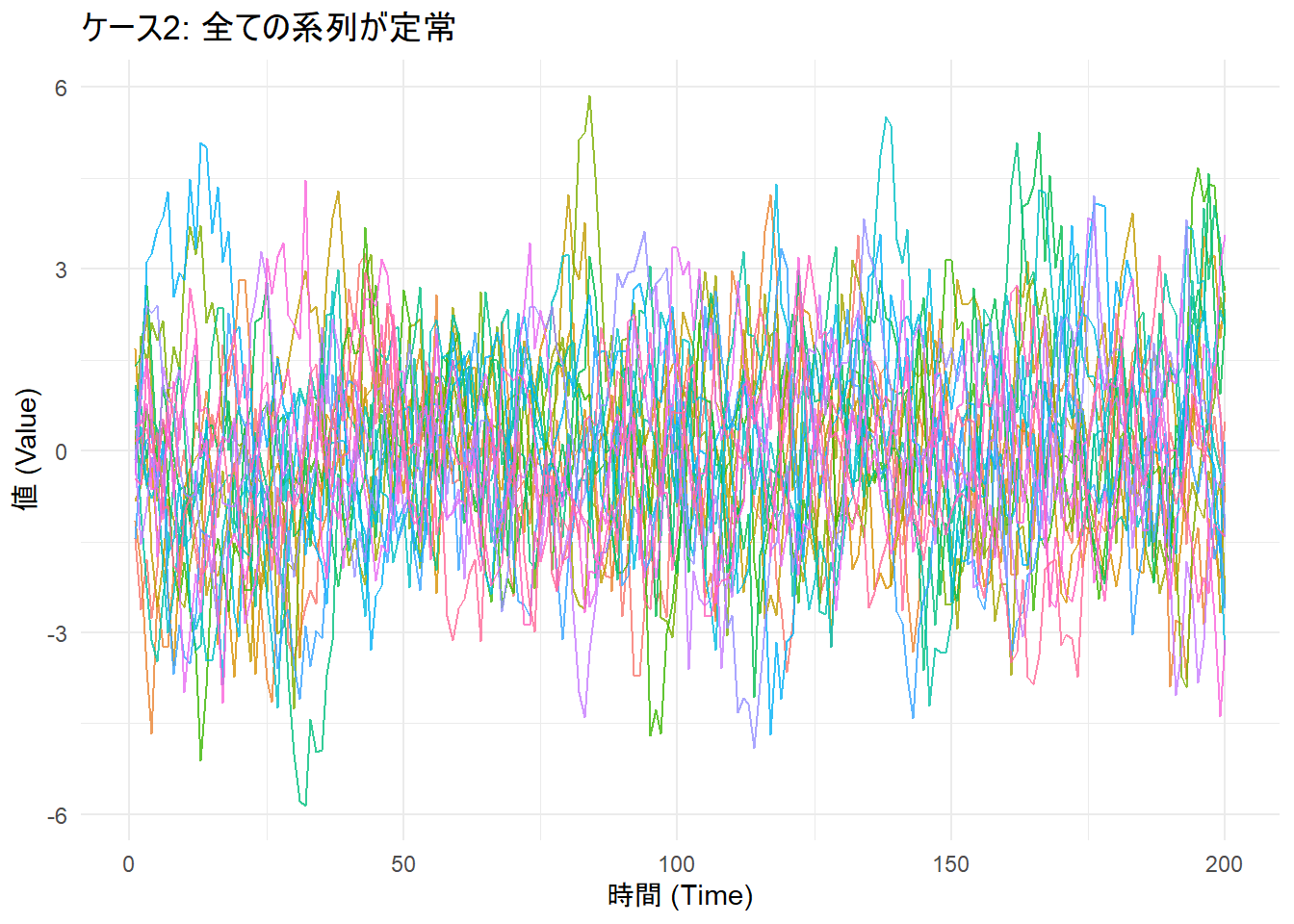
全ての系列が定常なAR(1)過程(\(y_t = 0.8 \times y_{t-1} + \epsilon_t\))に従うデータを生成します。この場合、対立仮説が真であるため、検定は棄却されるはずです。なお、本サンプルは同質性の仮定が満たされた時系列データになります。
データ生成と可視化
set.seed(seed)
# 自己回帰係数
rho_st <- 0.8
# データ生成
y_st <- matrix(0, nrow = T, ncol = N)
y_st[1, ] <- rnorm(N, mean = 0, sd = 1)
# 定常AR(1)過程を生成
for (t in 2:T) {
y_st[t, ] <- rho_st * y_st[t - 1, ] + rnorm(N, mean = 0, sd = 1)
}
# ロング形式に変換
panel_data_st <- as.data.frame(y_st) %>%
mutate(time = 1:T) %>%
pivot_longer(cols = -time, names_to = "id", values_to = "value")
# プロット
ggplot(panel_data_st, aes(x = time, y = value, group = id, color = id)) +
geom_line(alpha = 0.8, show.legend = FALSE) +
labs(
title = "ケース2: 全ての系列が定常",
x = "時間 (Time)", y = "値 (Value)"
) +
theme_minimal()パネル単位根検定の実行
# パネルデータフレームに変換
pdata_st <- pdata.frame(panel_data_st, index = c("id", "time"))
# LLC検定
llc_test_st <- purtest(value ~ 1, data = pdata_st, test = "levinlin")
cat("--- LLC検定の結果 ---\n")
print(llc_test_st)
# IPS検定
ips_test_st <- purtest(value ~ 1, data = pdata_st, test = "ips")
cat("--- IPS検定の結果 ---\n")
print(ips_test_st)--- LLC検定の結果 ---
Levin-Lin-Chu Unit-Root Test (ex. var.: Individual Intercepts)
data: value ~ 1
z = -15.158, p-value < 2.2e-16
alternative hypothesis: stationarity
--- IPS検定の結果 ---
Im-Pesaran-Shin Unit-Root Test (ex. var.: Individual Intercepts)
data: value ~ 1
Wtbar = -18.114, p-value < 2.2e-16
alternative hypothesis: stationarity考察: LLC検定、IPS検定ともにp値は設定した有意水準を下回っており(< 2.2e-16)、帰無仮説は棄却されます。これにより、パネルデータ全体が定常であると結論付けられます。これはデータ生成の過程と一致しており、正しい結果です。
ケース3: 単位根と定常系列が混在する場合
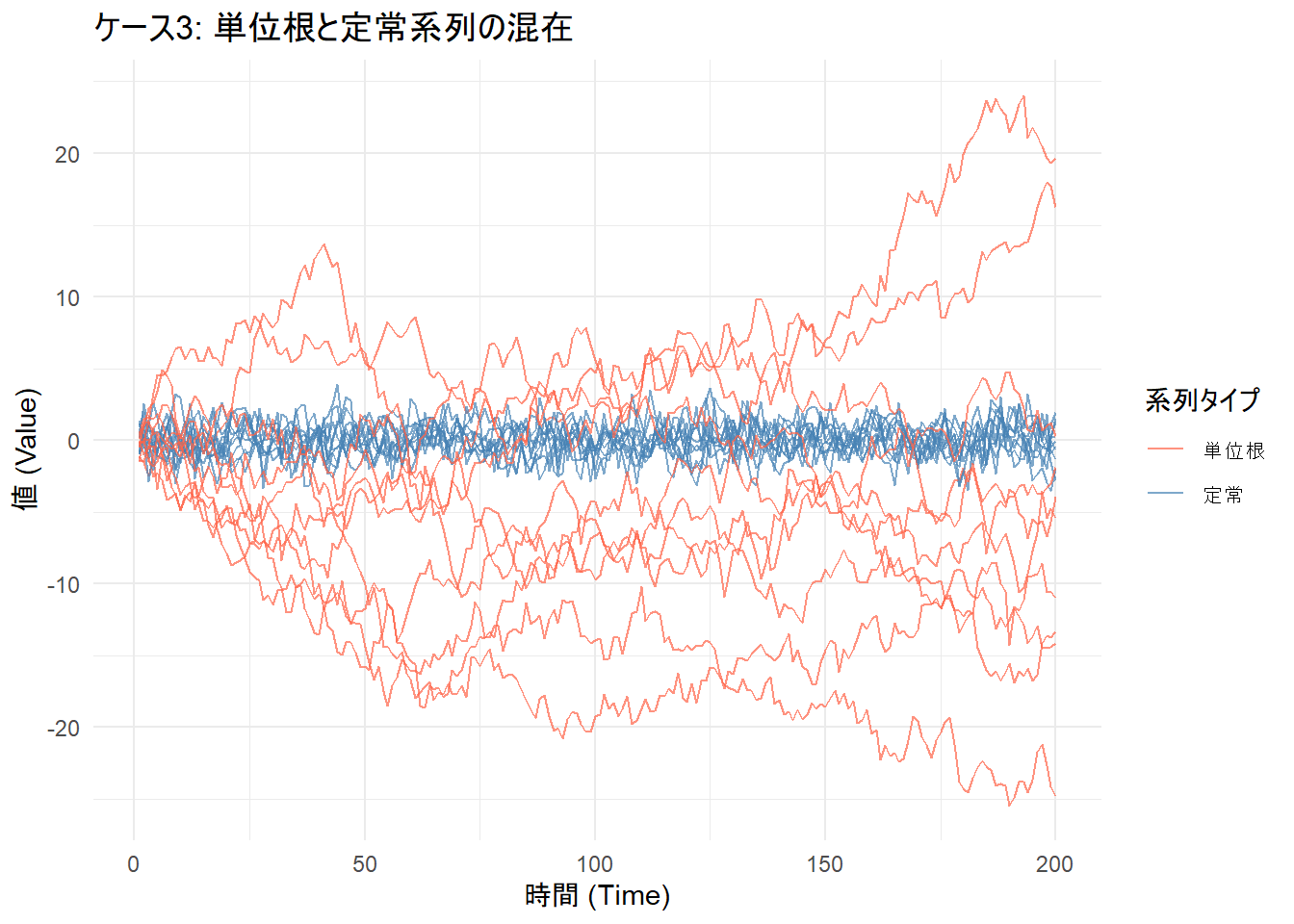
パネルの半分(10系列)が単位根、もう半分(10系列)が定常過程に従うデータを生成します。
データ生成と可視化
set.seed(seed)
N_rw <- 10 # 単位根を持つ系列の数
N_st <- 10 # 定常な系列の数
rho_mix <- 0.5 # 定常系列の自己回帰係数
# 単位根データの生成
y_mix_rw <- matrix(0, nrow = T, ncol = N_rw)
y_mix_rw[1, ] <- rnorm(N_rw)
for (t in 2:T) {
y_mix_rw[t, ] <- y_mix_rw[t - 1, ] + rnorm(N_rw)
}
# 定常データの生成
y_mix_st <- matrix(0, nrow = T, ncol = N_st)
y_mix_st[1, ] <- rnorm(N_st)
for (t in 2:T) {
y_mix_st[t, ] <- rho_mix * y_mix_st[t - 1, ] + rnorm(N_st)
}
# データを結合
y_mix <- cbind(y_mix_rw, y_mix_st)
colnames(y_mix) <- paste0("id_", 1:(N_rw + N_st))
# ロング形式に変換し、系列のタイプ(単位根か定常か)を示す列を追加
panel_data_mix <- as.data.frame(y_mix) %>%
mutate(time = 1:T) %>%
pivot_longer(cols = -time, names_to = "id", values_to = "value") %>%
mutate(type = ifelse(as.numeric(sub("id_", "", id)) <= N_rw, "単位根", "定常"))
# プロット(系列のタイプで色分け)
ggplot(panel_data_mix, aes(x = time, y = value, group = id, color = type)) +
geom_line(alpha = 0.7) +
labs(
title = "ケース3: 単位根と定常系列の混在",
x = "時間 (Time)", y = "値 (Value)", color = "系列タイプ"
) +
theme_minimal() +
scale_color_manual(values = c("単位根" = "tomato", "定常" = "steelblue"))パネル単位根検定の実行
# パネルデータフレームに変換
pdata_mix <- pdata.frame(panel_data_mix, index = c("id", "time"))
# LLC検定
llc_test_mix <- purtest(value ~ 1, data = pdata_mix, test = "levinlin")
cat("--- LLC検定の結果 ---\n")
print(llc_test_mix)
# IPS検定
ips_test_mix <- purtest(value ~ 1, data = pdata_mix, test = "ips")
cat("--- IPS検定の結果 ---\n")
print(ips_test_mix)--- LLC検定の結果 ---
Levin-Lin-Chu Unit-Root Test (ex. var.: Individual Intercepts)
data: value ~ 1
z = -6.8946, p-value = 2.7e-12
alternative hypothesis: stationarity
--- IPS検定の結果 ---
Im-Pesaran-Shin Unit-Root Test (ex. var.: Individual Intercepts)
data: value ~ 1
Wtbar = -19.21, p-value < 2.2e-16
alternative hypothesis: stationarity考察: このケースでは、LLC検定とIPS検定の両方が帰無仮説を棄却しました。しかし、両者の対立仮説の意味が異なることに注意が必要です。
- LLC検定: 対立仮説「全ての系列が共通の定常過程に従う」は、データ生成の仕方(半分は単位根)と矛盾します。それにもかかわらず棄却されたのは、パネル内に定常な系列が十分に存在し、検定統計量全体を押し下げたためと考えられます。しかし、この結果を「全ての系列が定常である」と解釈するのは誤りです。
- IPS検定: 対立仮説「一部の系列が定常過程に従う」は、データ生成の仕方と完全に一致します。したがって、この場合のIPS検定の結果は、データの構造を正しく捉えていると言えます。
このシミュレーションから、パネル内に異質性(単位根と定常の混在など)が疑われる場合は、IPS検定を用いる方がより適切であることがわかります。
まとめ
- LLC検定は、パネル内の全ての系列が同じように振る舞う(同質性)と仮定できる場合に有用です。
- IPS検定は、系列ごとに振る舞いが異なる(異質性)可能性がある場合により適しています。
以上です。