Rでブレント法

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)

# -----------------------------------------------------------------
# 1. シミュレーションの対象となる関数を定義 (二分法、はさみうち法と同じ)
# -----------------------------------------------------------------
# f(x) = x^3 - x - 1
f <- function(x) {
  return(x^3 - x - 1)
}

# -----------------------------------------------------------------
# 2. ブレント法のシミュレーションを行う関数を定義
# -----------------------------------------------------------------
brent_simulation <- function(func, a, b, tol = 1e-9, max_iter = 30) {
  fa <- func(a)
  fb <- func(b)

  if (fa * fb >= 0) {
    stop("初期区間[a, b]でf(a)とf(b)の符号が同じです。")
  }

  # b を常に最良近似解とするための入れ替え
  if (abs(fa) < abs(fb)) {
    temp <- a
    a <- b
    b <- temp
    temp <- fa
    fa <- fb
    fb <- temp
  }

  c <- a # c は前のb (contrapoint)
  fc <- fa
  d <- b - a # d は今回のステップ幅
  e <- d # e は前回のステップ幅

  cat("--- ブレント法シミュレーション開始 ---\n\n")
  cat(sprintf("対象関数: x^3 - x - 1\n"))
  cat(sprintf("初期区間: [%.1f, %.1f], 許容誤差: %e\n\n", a, b, tol))

  history <- data.frame(
    iter = integer(), a = double(), b = double(),
    s = double(), fs = double(), method = character()
  )

  for (i in 1:max_iter) {
    # bが最良近似解なので、f(b)が0に十分近ければ収束
    if (abs(fb) < tol || b == a) {
      cat(sprintf("\n--- 収束しました (反復 %d 回) ---\n\n", i - 1))
      break
    }

    # 3点が異なる場合、逆2次補間を試す
    if (fa != fc && fb != fc) {
      s <- (a * fb * fc / ((fa - fb) * (fa - fc))) +
        (b * fa * fc / ((fb - fa) * (fb - fc))) +
        (c * fa * fb / ((fc - fa) * (fc - fb)))
      method <- "逆2次補間"
    } else {
      # そうでなければ、はさみうち法を試す
      s <- b - fb * (b - a) / (fb - fa)
      method <- "はさみうち法"
    }

    # ----- 妥当性チェックと安全装置 -----
    # 1. sが区間の外 or 収束が遅すぎるか？
    condition1 <- (s < (3 * a + b) / 4 || s > b)
    # 2. 前回のステップ幅eに比べて今回のステップ幅dが十分小さくなっていないか？
    condition2 <- abs(s - b) >= abs(e / 2)
    # 3. 前回のステップ幅eが許容誤差より小さい（ほぼ収束している）か？
    condition3 <- abs(e) < tol
    # 4. 今回のステップ幅dが許容誤差より小さいか？
    condition4 <- abs(d) < tol

    # 上記のいずれかに該当する場合、計算したsを棄却して二分法に切り替える
    if (condition1 || condition2 || condition3 || condition4) {
      s <- (a + b) / 2
      d <- s - b
      e <- d
      method <- "二分法" # 手法を上書き
    } else {
      e <- d
      d <- s - b
    }

    fs <- func(s)

    cat(sprintf("【反復 %d回目】使用手法: %s\n", i, method))
    cat(sprintf("  探索点 s = %.8f, f(s) = %.2e\n", s, fs))

    history <- rbind(history, data.frame(
      iter = i, a = a, b = b, s = s, fs = fs, method = method
    ))

    # 次の反復のための変数の更新
    c <- b
    fc <- fb

    if (fa * fs < 0) {
      b <- s
      fb <- fs
    } else {
      a <- s
      fa <- fs
    }

    # bが最良近似解であり続けるように、必要ならaとbを入れ替える
    if (abs(fa) < abs(fb)) {
      temp <- a
      a <- b
      b <- temp
      temp <- fa
      fa <- fb
      fb <- temp
    }
  }

  if (i == max_iter) {
    cat("\n--- 最大反復回数に達しました ---\n")
  }

  cat(sprintf("最終的な解の近似値 c = %.8f\n", b))
  cat(sprintf("そのときの関数値 f(c) = %e\n", fb))

  return(history)
}

# -----------------------------------------------------------------
# 3. シミュレーションの実行
# -----------------------------------------------------------------
simulation_history_brent <- brent_simulation(f, 1.0, 2.0)

# -----------------------------------------------------------------
# 4. ggplot2による結果の可視化
# -----------------------------------------------------------------

# 最終的な解の値を取得
final_solution_value <- tail(simulation_history_brent, 1)$s

brent_process_plot <- ggplot(simulation_history_brent, aes(x = iter, y = s)) +

  # 真の解の位置を水平線で示す
  geom_hline(yintercept = final_solution_value, linetype = "dashed", color = "red", linewidth = 1) +
  geom_text(aes(x = 0.5, y = final_solution_value, label = sprintf("真の解\n(約 %.6f)", final_solution_value)),
    color = "red", hjust = 0, vjust = -0.2
  ) +

  # 近似解の推移を線で結ぶ
  geom_line(color = "gray50", linewidth = 1) +

  # 各ステップの近似解と使用した手法を点と形で示す
  geom_point(aes(shape = method, color = method), size = 5, stroke = 1.5) +

  # 手法ごとに色と形を明示的に設定
  scale_color_manual(
    name = "使用された手法",
    values = c("二分法" = "#00BFC4", "はさみうち法" = "#F8766D", "逆2次補間" = "#7CAE00")
  ) +
  scale_shape_manual(
    name = "使用された手法",
    values = c("二分法" = 1, "はさみうち法" = 2, "逆2次補間" = 0)
  ) +

  # 軸ラベルとタイトル
  labs(
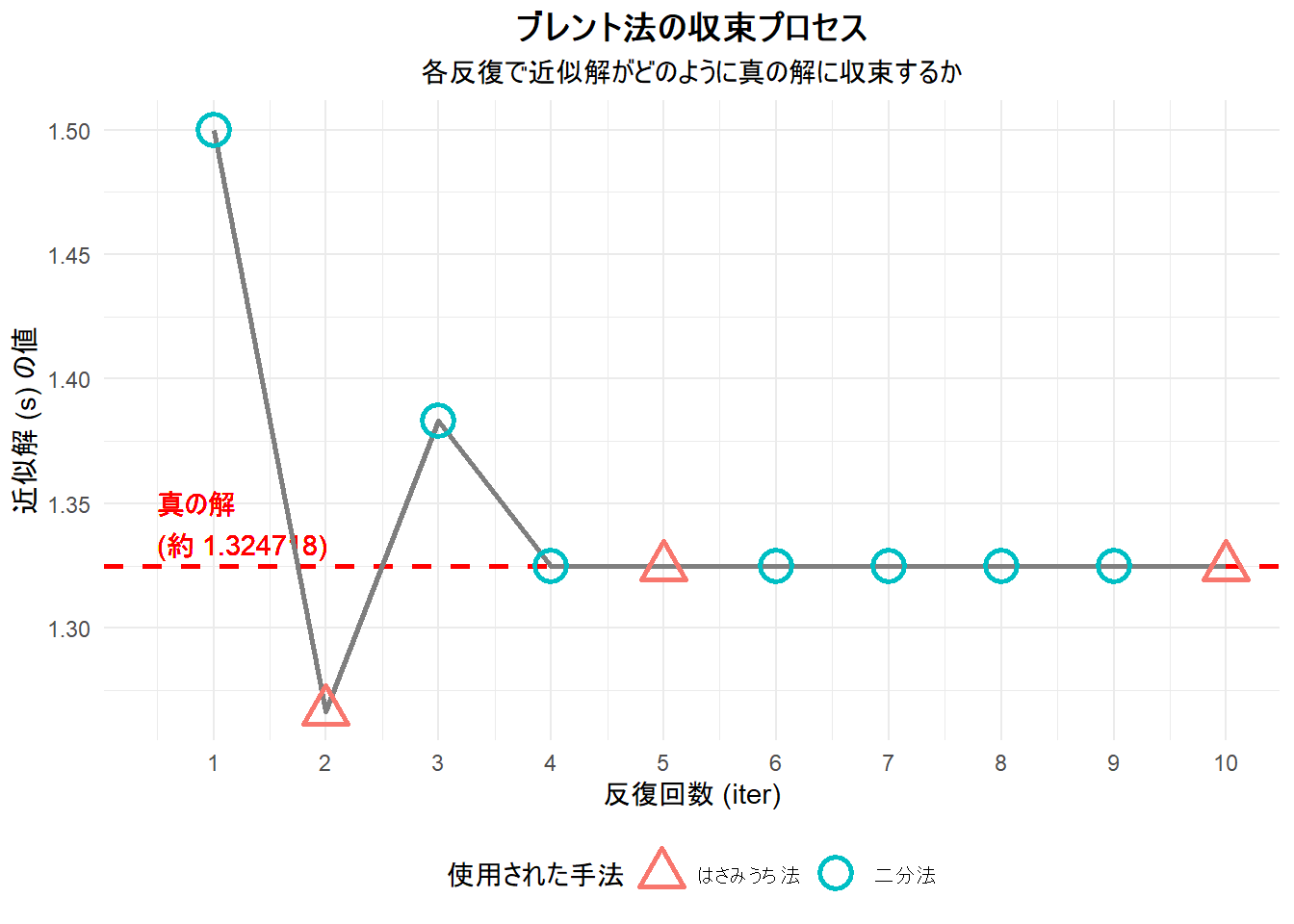
    title = "ブレント法の収束プロセス",
    subtitle = "各反復で近似解がどのように真の解に収束するか",
    x = "反復回数 (iter)",
    y = "近似解 (s) の値"
  ) +
  scale_x_continuous(breaks = 1:nrow(simulation_history_brent)) + # X軸の目盛りを整数に
  theme_minimal(base_family = "sans") +
  theme(
    plot.title = element_text(hjust = 0.5, face = "bold"),
    plot.subtitle = element_text(hjust = 0.5),
    legend.position = "bottom"
  )

# 新しいプロットを表示
print(brent_process_plot)