Rでボンフェローニ補正

Rで ボンフェローニ補正 を確認します。

1. ボンフェローニ補正とは？

なぜ補正が必要か：多重比較の問題

統計的検定では、「本当は差がないのに、偶然のデータのばらつきによって『有意な差がある』と誤って結論づけてしまう確率」を第一種の過誤 (Type I Error) と呼びます。この確率をコントロールするために、私たちは有意水準α（アルファ、通常は0.05や0.01）を設定します。1回の検定であれば、第一種の過誤を犯す確率はα以下に抑えられます。

しかし、同じデータセットに対して何度も検定を繰り返す（多重比較）と、問題が生じます。例えば、有意水準5%（α=0.05）で検定を行うと、20回に1回の確率で偶然有意な結果が出ることになります。もし3つのグループ（A, B, C）の平均値を比較するために、3つのペア（A vs B, A vs C, B vs C）で検定を行うと、少なくとも1回でも第一種の過誤を犯す確率（これをFamily-Wise Error Rate, FWER と呼びます）は5%よりも大きくなってしまいます。

検定回数を n とすると、FWERは以下の式で近似できます。

FWER ≈ 1 - (1 - α)^n

例えば、α=0.05で3回検定を行うと、FWERは約14.3% (1 - (1 - 0.05)^3 ≈ 0.143) にもなり、設定した5%を大きく超えてしまいます。これが多重比較の問題です。

ボンフェローニ補正の考え方

ボンフェローニ補正は、この多重比較の問題を解決するための方法の一つです。考え方は非常に単純です。

「個々の検定の有意水準を、検定の回数で割った値に設定し直す」

これにより、全体のFWERが設定したαを超えないようにコントロールします。

元の有意水準: α
検定（比較）の回数: n
補正後の有意水準: α' = α / n

例えば、α=0.05、検定回数n=3の場合、個々の検定は 0.05 / 3 ≈ 0.0167 という非常に厳しい水準でなければ「有意差あり」と判定されなくなります。

実務的には、算出したp値に検定回数 n を掛けた「調整済みp値 (Adjusted p-value)」を求め、この値と元の有意水準α（例: 0.05）を比較する方法が簡便です。

2. R言語によるシミュレーション

それでは、ボンフェローニ補正の効果をシミュレーションで確認してみましょう。ここでは、「平均値に全く差がない4つのグループ」のデータを生成し、多重比較を行うという状況を何度も繰り返します。本来差はないので、もし「有意差あり」という結果が出たら、それは第一種の過誤です。

このシミュレーションを通して、以下の2点を確認します。

補正を行わない場合、FWERが設定した有意水準（5%）を大幅に上回ってしまうこと。
ボンフェローニ補正を行うと、FWERが5%程度に適切にコントロールされること。

2.1. 準備

まず、必要なライブラリを読み込みます。

library(tidyverse)

seed <- 20250706

2.2. シミュレーションの実行

4つのグループ間のすべてのペアでt検定を行います。データ生成と検定を2000回繰り返し、第一種の過誤が起きた割合（FWER）を計算します。

# シミュレーションの設定
set.seed(seed) # 結果を再現可能にするための乱数シード
n_sim <- 2000 # シミュレーション回数
n_groups <- 4 # グループ数
n_sample <- 30 # 各グループのサンプルサイズ
alpha <- 0.05 # 有意水準

# 比較の組み合わせの数を計算 (4つのグループから2つを選ぶ組み合わせ)
n_comparisons <- choose(n_groups, 2)
cat("グループ数:", n_groups, "\n")
cat("比較の回数:", n_comparisons, "\n")

# シミュレーションの実行
# replicate関数で同じ処理をn_sim回繰り返す
sim_results <- replicate(n_sim, {
  # 【データ生成】
  # 全グループの母平均は0、標準偏差は1で、差がない状況を作る
  sim_data <- data.frame(
    value = rnorm(n_groups * n_sample, mean = 0, sd = 1),
    group = factor(rep(1:n_groups, each = n_sample))
  )

  # 【補正なしの場合】
  # pairwise.t.testで全ペアのt検定を一括実行
  # p.adjust.method = "none"で補正なしのp値を取得
  p_raw <- pairwise.t.test(sim_data$value, sim_data$group, p.adjust.method = "none")$p.value

  # 少なくとも1つのp値がalphaを下回るか（=第一種の過誤が発生したか）
  error_no_correction <- any(p_raw < alpha, na.rm = TRUE)

  # 【ボンフェローニ補正ありの場合】
  # p.adjust.method = "bonferroni"で調整済みp値を取得
  p_bonf <- pairwise.t.test(sim_data$value, sim_data$group, p.adjust.method = "bonferroni")$p.value

  # 少なくとも1つの調整済みp値がalphaを下回るか
  error_with_correction <- any(p_bonf < alpha, na.rm = TRUE)

  # 2つの結果をベクトルで返す
  c(no_correction = error_no_correction, bonferroni = error_with_correction)
})

# FWER（第一種の過誤が起きた割合）を計算
# sim_resultsは行が手法、列が試行回数の行列になっている
# rowMeansで行ごとの平均を計算する (TRUE=1, FALSE=0として計算される)
fwer <- rowMeans(sim_results)

# 結果の表示
print(fwer)

グループ数: 4 
比較の回数: 6 
no_correction    bonferroni 
        0.206         0.047

シミュレーション結果から、以下のことがわかります。

補正なし (no_correction): FWERは約 20.6% となり、本来コントロールしたかった5%を大幅に超えています。6回の検定を繰り返すと、5回に1回程度は誤った結論を出してしまうことになります。
ボンフェローニ補正 (bonferroni): FWERは約 4.7% となり、目標の有意水準5%に近い値にしっかりとコントロールされています。

2.3. 結果の可視化

この結果をggplot2で可視化すると、ボンフェローニ補正の効果が一目瞭然になります。

# プロット用のデータフレームを作成
plot_data <- data.frame(
  Method = c("補正なし", "ボンフェローニ補正"),
  FWER = fwer
) %>%
  # グラフの表示順を固定
  mutate(Method = factor(Method, levels = c("補正なし", "ボンフェローニ補正")))

# ggplotで棒グラフを作成
ggplot(plot_data, aes(x = Method, y = FWER, fill = Method)) +
  geom_col(width = 0.6, alpha = 0.8) +
  # 目標の有意水準0.05のラインを引く
  geom_hline(yintercept = alpha, color = "darkred", linetype = "dashed", linewidth = 1.0) +
  # 棒グラフの上に数値を表示
  geom_text(aes(label = scales::percent(FWER, accuracy = 0.1)), vjust = -0.5, size = 5) +
  # Y軸をパーセント表示に
  scale_y_continuous(labels = scales::percent_format(accuracy = 1), limits = c(0, 0.3)) +
  scale_fill_manual(values = c("補正なし" = "#d95f02", "ボンフェローニ補正" = "#1b9e77")) +
  labs(
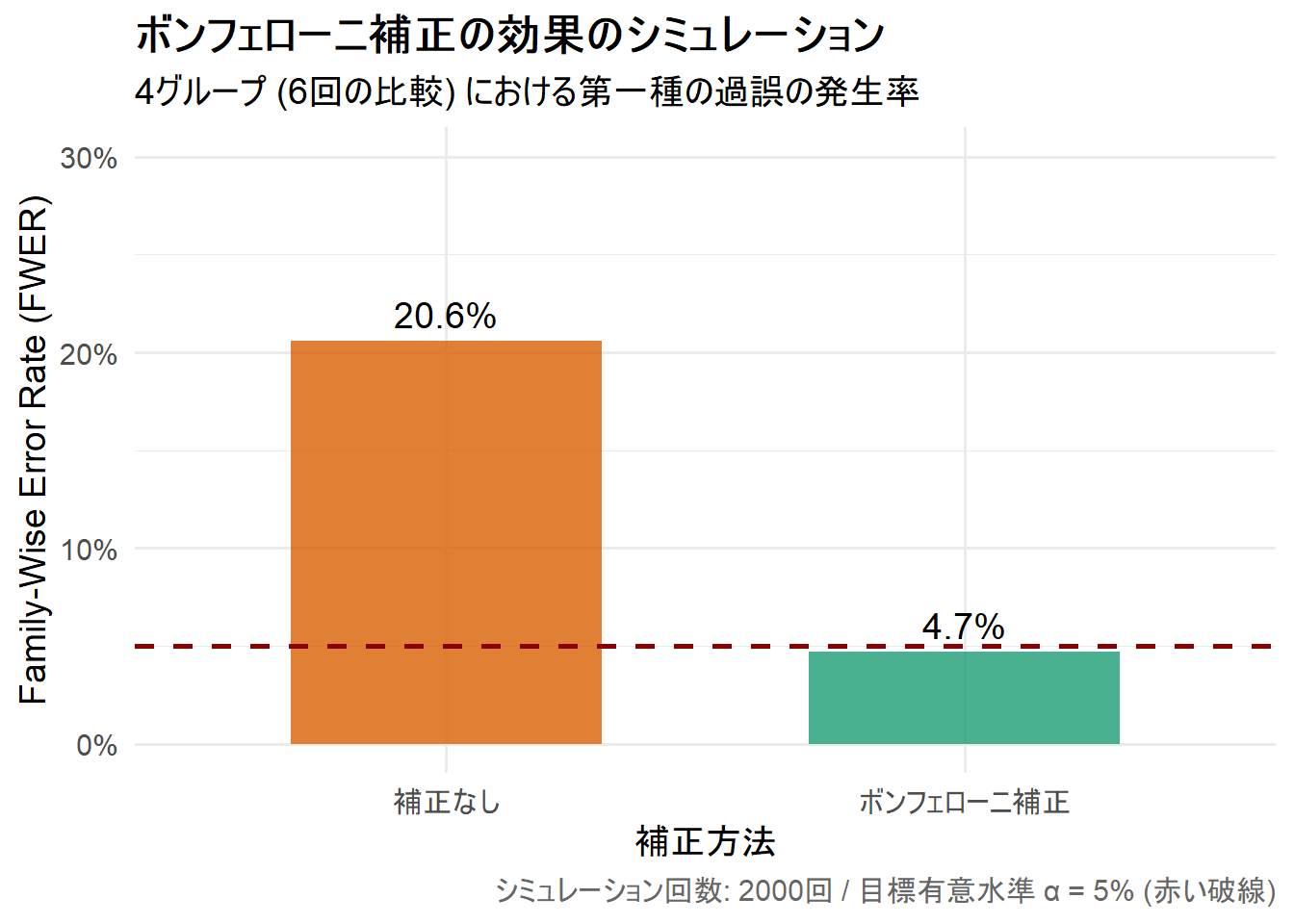
    title = "ボンフェローニ補正の効果のシミュレーション",
    subtitle = paste0(n_groups, "グループ (", n_comparisons, "回の比較) における第一種の過誤の発生率"),
    x = "補正方法",
    y = "Family-Wise Error Rate (FWER)",
    caption = paste0("シミュレーション回数: ", n_sim, "回 / 目標有意水準 α = 5% (赤い破線)")
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "none",
    plot.title = element_text(face = "bold"),
    plot.caption = element_text(color = "grey40")
  )