Rで主成分分析

Rで 主成分分析 を試みます。

1. 主成分分析とは

主成分分析（Principal Component Analysis, PCA）は、多変量解析の手法の一つです。多数の変量（量的変数）からなるデータを、より少ない指標（主成分）に要約することを目的とします。これにより、データの次元を削減し、可視化や解釈を容易にします。

主成分分析の根底にある考え方は、「データのばらつき（分散）が最も大きい方向」を新しい軸として見つけ出すことです。この新しい軸が「第1主成分」となります。次に、第1主成分と直交する方向の中で、データのばらつきが最大になる方向を「第2主成分」として見つけます。これを繰り返し、元の変数の数だけ主成分を計算することができます。

手順は以下の通りです。

データの準備: n個のサンプルとp個の変数からなるデータ行列 X (n × p 行列) を用意します。
データの標準化: 各変数の単位やスケールが異なると、分散が大きい変数に分析が引きずられてしまいます。そのため、各変数の平均を0、分散を1に変換（標準化）します。標準化後のデータ行列を Z とします。
共分散行列（または相関行列）の計算: 変数間の関係性を表す行列を計算します。データを標準化した場合、共分散行列は相関行列 R と一致します。相関行列 R は (1/(n-1)) * t(Z) %*% Z で計算されます（t(Z)はZの転置行列）。
固有値分解: 相関行列 R の固有値と固有ベクトルを求めます。
R * v = λ * v
ここで、
- λ (ラムダ): 固有値。各主成分が説明する分散の大きさを表します。大きい順に λ1 >= λ2 >= ... >= λp >= 0 となります。
- v: 固有ベクトル。各主成分の方向（軸）を定義します。これは「主成分負荷量（loading）」と呼ばれ、元の変数が各主成分にどれだけ影響を与えているかを示します。
主成分の選択: 計算されたp個の主成分のうち、どこまでを採用するかを決定します。判断基準として以下が用いられます。
- 寄与率: 全分散のうち、各主成分がどれだけの割合を説明しているかを示す指標です (寄与率 = λk / sum(λ)）。
- 累積寄与率: 第1主成分から第k主成分までの寄与率の合計です。一般的に、累積寄与率が70%〜80%に達するまでの主成分を採用することが多いです。
- スクリープロット: 固有値を大きい順に並べた棒グラフ。プロットの傾きが緩やかになる手前（“肘”の部分）までを採用するというカイザー基準などがあります。
主成分得点の計算: 元のデータ（標準化後）を、新しく見つけた主成分軸に射影して、各サンプルの新しい座標値を計算します。これが「主成分得点（score）」です。
主成分得点行列 Y = Z * V
ここで、Vは固有ベクトルを列として並べた行列です。Yの第1列が各サンプルの第1主成分得点、第2列が第2主成分得点となります。

この主成分得点を用いることで、元のp次元のデータを、より低次元（例えば2次元）のグラフにプロットして、データの構造を視覚的に把握することができます。

2. シミュレーションのシナリオ

シナリオ: 「とある高校の生徒たちの学力傾向を探る」

とある進学校に、100人の生徒が在籍しています。先日、全生徒が5教科（国語、社会、数学、理科、英語）の統一模試を受けました。

教員は、この5教科の点数という多次元的なデータを見て、生徒一人ひとりの学力特性をよりシンプルに把握したいと考えています。

単純に合計点が高い生徒は誰か？ ( 総合学力 )
文系科目（国語、社会）が得意な生徒と、理系科目（数学、理科）が得意な生徒の分布はどうなっているか？ ( 文理傾向 )

これらの潜在的な特徴を明らかにするため、主成分分析を用いることにしました。

データの想定:

国語と社会の点数には、強い正の相関がある（文系的素養）。
数学と理科の点数にも、強い正の相関がある（理系的素養）。
英語は、文系・理系両方の科目とある程度の相関がある。
全体として「総合学力」が高い生徒は全教科で点数が高く、低い生徒は全般的に低い傾向がある。

このシナリオに基づき、主成分分析によって5次元の成績データを2次元（第1主成分、第2主成分）に要約し、「総合学力」と「文理傾向」という2つの軸で生徒たちの分布を可視化します。

3. R言語によるシミュレーション

まず、シナリオに沿ったデータを生成し、その後、標準化→相関行列→固有値分解→主成分得点計算の手順で主成分分析を行います。

# 必要なパッケージを読み込む
library(MASS)
library(ggplot2)
library(dplyr)

# 0. シナリオに基づいたデータ生成
# ---------------------------------
seed <- 20250722
set.seed(seed) # 結果を再現可能にするための乱数シード

# 生徒数
num_students <- 100

# 各教科の相関行列を定義
# 国語-社会、数学-理科の相関を高く設定
cor_matrix <- matrix(c(
  1.0, 0.7, 0.3, 0.2, 0.5, # 国語
  0.7, 1.0, 0.2, 0.1, 0.4, # 社会
  0.3, 0.2, 1.0, 0.8, 0.6, # 数学
  0.2, 0.1, 0.8, 1.0, 0.5, # 理科
  0.5, 0.4, 0.6, 0.5, 1.0 # 英語
), nrow = 5, ncol = 5)

# 教科名
subject_names <- c("国語", "社会", "数学", "理科", "英語")
colnames(cor_matrix) <- rownames(cor_matrix) <- subject_names

# 平均点と標準偏差
mu <- c(65, 62, 70, 68, 75)
sds <- c(15, 16, 18, 17, 20)
cov_matrix <- diag(sds) %*% cor_matrix %*% diag(sds) # 共分散行列に変換

# 多変量正規分布に従うデータを生成
student_scores <- mvrnorm(n = num_students, mu = mu, Sigma = cov_matrix)

# 100点満点を超えたり、0点を下回ったりする値を丸める
student_scores[student_scores > 100] <- 100
student_scores[student_scores < 0] <- 0
student_scores <- round(student_scores)

# データフレームに変換
scores_df <- as.data.frame(student_scores)
colnames(scores_df) <- subject_names

cat("--- 生成された成績データの一部を確認 ---\n\n")
print(head(scores_df))
print(tail(scores_df))
cat("\n")

# 1. データの標準化
# --------------------
scaled_scores <- scale(scores_df)

cat("--- 標準化された成績データの一部を確認 ---\n\n")
print(head(scaled_scores))
print(tail(scaled_scores))
cat("\n")


# 2. 相関行列の計算
# --------------------
# 標準化されたデータから相関行列を計算
cor_matrix_from_data <- cor(scaled_scores)

cat("--- データから計算された相関行列 ---\n\n")
print(round(cor_matrix_from_data, 2))
cat("\n")


# 3. 固有値分解
# --------------------
eigen_result <- eigen(cor_matrix_from_data)

# 固有値
eigen_values <- eigen_result$values

# 固有ベクトル（主成分負荷量）
eigen_vectors <- eigen_result$vectors
colnames(eigen_vectors) <- paste0("PC", 1:5)
rownames(eigen_vectors) <- subject_names

cat("--- 固有値 ---\n\n")
print(eigen_values)
cat("\n")

cat("--- 固有ベクトル（主成分負荷量） ---\n\n")
print(eigen_vectors)
cat("\n")


# 4. 寄与率と累積寄与率の計算
# ------------------------------
# 寄与率
contribution_ratio <- eigen_values / sum(eigen_values)
# 累積寄与率
cumulative_ratio <- cumsum(contribution_ratio)

# 結果をデータフレームにまとめる
contribution_df <- data.frame(
  PC = paste0("PC", 1:5),
  Eigenvalue = eigen_values,
  ContributionRatio = contribution_ratio,
  CumulativeRatio = cumulative_ratio
)

cat("--- 各主成分の寄与率 ---\n\n")
print(contribution_df)
cat("\n")


# 5. 主成分得点の計算
# ------------------------------
# 主成分得点 = 標準化データ %*% 固有ベクトル
principal_component_scores <- scaled_scores %*% eigen_vectors
colnames(principal_component_scores) <- paste0("PC", 1:5)

cat("--- 計算された主成分得点の一部を確認 ---\n\n")
print(head(principal_component_scores))
print(tail(principal_component_scores))
cat("\n")

--- 生成された成績データの一部を確認 ---

  国語 社会 数学 理科 英語
1   63   78   72   65   79
2   77   64   79   67  100
3   81   63   65   48   73
4   79   99   99  100   99
5   24   12   60   70   61
6   77   81   71   56   56
    国語 社会 数学 理科 英語
95    53   60   57   73   41
96    77   66   83   82   94
97    50   41   36   51   54
98    50   32   65   71   66
99    52   46   52   32   43
100   51   47   62   71   58

--- 標準化された成績データの一部を確認 ---

           国語       社会       数学        理科        英語
[1,] -0.0337791  1.0053433  0.1789622 -0.18167345  0.37346235
[2,]  0.8756582  0.1779003  0.5741470 -0.06521611  1.50516643
[3,]  1.1354974  0.1187972 -0.2162225 -1.17156087  0.05011832
[4,]  1.0055778  2.2465079  1.7032462  1.85633004  1.45127576
[5,] -2.5672115 -2.8954597 -0.4984973  0.10946990 -0.59656972
[6,]  0.8756582  1.1826526  0.1225073 -0.70573150 -0.86602308
             国語        社会       数学       理科       英語
 [95,] -0.6833771 -0.05851205 -0.6678622  0.2841559 -1.6743831
 [96,]  0.8756582  0.29610641  0.7999668  0.8082140  1.1818224
 [97,] -0.8782566 -1.18147050 -1.8534164 -0.9968749 -0.9738044
 [98,] -0.8782566 -1.71339819 -0.2162225  0.1676986 -0.3271164
 [99,] -0.7483369 -0.88595512 -0.9501370 -2.1032196 -1.5666018
[100,] -0.8132967 -0.82685204 -0.3855874  0.1676986 -0.7582417

--- データから計算された相関行列 ---

     国語 社会 数学 理科 英語
国語 1.00 0.76 0.27 0.17 0.52
社会 0.76 1.00 0.23 0.06 0.38
数学 0.27 0.23 1.00 0.82 0.65
理科 0.17 0.06 0.82 1.00 0.55
英語 0.52 0.38 0.65 0.55 1.00

--- 固有値 ---

[1] 2.7887076 1.4353838 0.3875742 0.2412646 0.1470697

--- 固有ベクトル（主成分負荷量） ---

           PC1         PC2         PC3        PC4        PC5
国語 0.4181742  0.51915547  0.03970157  0.6786222  0.3057836
社会 0.3653189  0.58146457 -0.41553276 -0.4970876 -0.3296628
数学 0.4928160 -0.37921099 -0.27068908 -0.3000237  0.6708537
理科 0.4337468 -0.49562088 -0.32665624  0.3830086 -0.5593065
英語 0.5105572 -0.05418046  0.80360403 -0.2359365 -0.1869502

--- 各主成分の寄与率 ---

   PC Eigenvalue ContributionRatio CumulativeRatio
1 PC1  2.7887076        0.55774152       0.5577415
2 PC2  1.4353838        0.28707677       0.8448183
3 PC3  0.3875742        0.07751484       0.9223331
4 PC4  0.2412646        0.04825292       0.9705861
5 PC5  0.1470697        0.02941394       1.0000000

--- 計算された主成分得点の一部を確認 ---

             PC1        PC2        PC3         PC4        PC5
[1,]  0.55321442  0.5689773 -0.1080767 -0.73405573 -0.1899036
[2,]  1.45430297  0.2910944  1.0362874 -0.04655068  0.3493680
[3,] -0.07089585  1.3185046  0.4772189  0.31585038  0.8088919
[4,]  3.62672180  0.1837596 -0.7947555 -0.57673657 -0.6000457
[5,] -2.63407587 -2.8492866  0.7210090  0.02937184 -0.1146032
[6,]  0.11033346  1.4925140 -0.9552353 -0.09637068  0.5166934
             PC1        PC2         PC3        PC4         PC5
 [95,] -1.367896 -0.1856557 -1.26039681  0.2695875 -0.48361804
 [96,]  1.822535 -0.1411775  0.38088992  0.2377591  0.03382603
 [97,] -2.641845  0.1067341  0.50085335  0.3953031 -0.38282928
 [98,] -1.194032 -1.4356297  0.41798216  0.4619851  0.11859300
 [99,] -2.816939  0.5839264  0.02372724 -0.2183098  0.89505535
[100,] -1.146575 -0.7988267 -0.24843665  0.2179089 -0.18682467

4. パッケージ関数との比較

1. prcomp {stats} による主成分分析

次に、Rの標準パッケージ stats に含まれる prcomp() 関数を使って同じ分析を行い、上記で実装(以降、スクラッチ実装)した結果と比較します。

# prcomp()関数による主成分分析
# -------------------------------
# scale. = TRUE オプションで、自動的にデータを標準化してくれます
pca_result_pkg <- prcomp(scores_df, scale. = TRUE)

cat("--- prcomp()関数による分析結果のサマリー ---\n\n")
summary(pca_result_pkg)
cat("\n")

# 結果の比較
# ------------
cat("--- スクラッチ実装とprcomp()の結果比較(固有値、主成分負荷量、主成分得点) ---\n\n")

# 比較1: 固有値
# prcompの結果では標準偏差(sdev)で保持されているため、2乗して分散（固有値）に変換します
prcomp_eigenvalues <- pca_result_pkg$sdev^2

comparison_eigenvalues <- data.frame(
  Scratch_Eigenvalues = eigen_values,
  prcomp_Eigenvalues = prcomp_eigenvalues
)
cat("1. 固有値の比較\n")
print(comparison_eigenvalues)
cat(paste0("\n結果は一致しているか → ", all.equal(eigen_values, prcomp_eigenvalues)))
cat("\n")

# 比較2: 主成分負荷量（固有ベクトル）
# prcompではrotationという名前で格納されています
prcomp_loadings <- pca_result_pkg$rotation

cat("\n2. 主成分負荷量の比較\n\n")
cat("--- スクラッチ実装の結果 ---\n")
print(eigen_vectors)
cat("\n--- prcomp()の結果 ---\n")
print(prcomp_loadings)
cat(paste0("\n結果は一致しているか(PC3を除く) → ", all.equal(eigen_vectors[, -3], prcomp_loadings[, -3])))
cat(paste0("\n結果は一致しているか(PC3のみ。符号反転後) → ", all.equal(-(eigen_vectors[, 3]), prcomp_loadings[, 3])))
cat("\n")

# 比較3: 主成分得点
# prcompではxという名前で格納されています
prcomp_scores <- pca_result_pkg$x

cat("\n3. 主成分得点の比較(表示は一部)\n\n")
cat("--- スクラッチ実装の結果 ---\n")
print(head(principal_component_scores))
print(tail(principal_component_scores))
cat("\n--- prcomp()の結果 ---\n")
print(head(prcomp_scores))
print(tail(prcomp_scores))
cat(paste0("\n結果は一致しているか(PC3を除く) → ", all.equal(principal_component_scores[, -3], prcomp_scores[, -3])))
cat(paste0("\n結果は一致しているか(PC3のみ。符号反転後) → ", all.equal(-(principal_component_scores[, 3]), prcomp_scores[, 3])))

--- prcomp()関数による分析結果のサマリー ---

Importance of components:
                          PC1    PC2     PC3     PC4     PC5
Standard deviation     1.6699 1.1981 0.62255 0.49119 0.38350
Proportion of Variance 0.5577 0.2871 0.07751 0.04825 0.02941
Cumulative Proportion  0.5577 0.8448 0.92233 0.97059 1.00000

--- スクラッチ実装とprcomp()の結果比較(固有値、主成分負荷量、主成分得点) ---

1. 固有値の比較
  Scratch_Eigenvalues prcomp_Eigenvalues
1           2.7887076          2.7887076
2           1.4353838          1.4353838
3           0.3875742          0.3875742
4           0.2412646          0.2412646
5           0.1470697          0.1470697

結果は一致しているか → TRUE

2. 主成分負荷量の比較

--- スクラッチ実装の結果 ---
           PC1         PC2         PC3        PC4        PC5
国語 0.4181742  0.51915547  0.03970157  0.6786222  0.3057836
社会 0.3653189  0.58146457 -0.41553276 -0.4970876 -0.3296628
数学 0.4928160 -0.37921099 -0.27068908 -0.3000237  0.6708537
理科 0.4337468 -0.49562088 -0.32665624  0.3830086 -0.5593065
英語 0.5105572 -0.05418046  0.80360403 -0.2359365 -0.1869502

--- prcomp()の結果 ---
           PC1         PC2         PC3        PC4        PC5
国語 0.4181742  0.51915547 -0.03970157  0.6786222  0.3057836
社会 0.3653189  0.58146457  0.41553276 -0.4970876 -0.3296628
数学 0.4928160 -0.37921099  0.27068908 -0.3000237  0.6708537
理科 0.4337468 -0.49562088  0.32665624  0.3830086 -0.5593065
英語 0.5105572 -0.05418046 -0.80360403 -0.2359365 -0.1869502

結果は一致しているか(PC3を除く) → TRUE
結果は一致しているか(PC3のみ。符号反転後) → TRUE

3. 主成分得点の比較(表示は一部)

--- スクラッチ実装の結果 ---
             PC1        PC2        PC3         PC4        PC5
[1,]  0.55321442  0.5689773 -0.1080767 -0.73405573 -0.1899036
[2,]  1.45430297  0.2910944  1.0362874 -0.04655068  0.3493680
[3,] -0.07089585  1.3185046  0.4772189  0.31585038  0.8088919
[4,]  3.62672180  0.1837596 -0.7947555 -0.57673657 -0.6000457
[5,] -2.63407587 -2.8492866  0.7210090  0.02937184 -0.1146032
[6,]  0.11033346  1.4925140 -0.9552353 -0.09637068  0.5166934
             PC1        PC2         PC3        PC4         PC5
 [95,] -1.367896 -0.1856557 -1.26039681  0.2695875 -0.48361804
 [96,]  1.822535 -0.1411775  0.38088992  0.2377591  0.03382603
 [97,] -2.641845  0.1067341  0.50085335  0.3953031 -0.38282928
 [98,] -1.194032 -1.4356297  0.41798216  0.4619851  0.11859300
 [99,] -2.816939  0.5839264  0.02372724 -0.2183098  0.89505535
[100,] -1.146575 -0.7988267 -0.24843665  0.2179089 -0.18682467

--- prcomp()の結果 ---
             PC1        PC2        PC3         PC4        PC5
[1,]  0.55321442  0.5689773  0.1080767 -0.73405573 -0.1899036
[2,]  1.45430297  0.2910944 -1.0362874 -0.04655068  0.3493680
[3,] -0.07089585  1.3185046 -0.4772189  0.31585038  0.8088919
[4,]  3.62672180  0.1837596  0.7947555 -0.57673657 -0.6000457
[5,] -2.63407587 -2.8492866 -0.7210090  0.02937184 -0.1146032
[6,]  0.11033346  1.4925140  0.9552353 -0.09637068  0.5166934
             PC1        PC2         PC3        PC4         PC5
 [95,] -1.367896 -0.1856557  1.26039681  0.2695875 -0.48361804
 [96,]  1.822535 -0.1411775 -0.38088992  0.2377591  0.03382603
 [97,] -2.641845  0.1067341 -0.50085335  0.3953031 -0.38282928
 [98,] -1.194032 -1.4356297 -0.41798216  0.4619851  0.11859300
 [99,] -2.816939  0.5839264 -0.02372724 -0.2183098  0.89505535
[100,] -1.146575 -0.7988267  0.24843665  0.2179089 -0.18682467

結果は一致しているか(PC3を除く) → TRUE
結果は一致しているか(PC3のみ。符号反転後) → TRUE

主成分負荷量の比較について、PC3のみ符号が反転していますが、ベクトルは同じ直線上にあり、軸としての役割は同じ、つまりベクトルの方向としては等価です。

以下で、固有ベクトル（主成分負荷量）の等価性を確認します。

2. ベクトルの内積による確認

2つのベクトルが同じ方向か真逆の方向を向いている場合、それらの単位ベクトル同士の内積は+1または-1になります。

# スクラッチ実装の固有ベクトル
v_scratch <- eigen_vectors
# prcomp()の固有ベクトル
v_prcomp <- pca_result_pkg$rotation

# 各主成分に対応するベクトル同士の内積を計算
# t(A) %*% B の対角成分は、AとBの対応する列ベクトルの内積になる
dot_products <- diag(t(v_scratch) %*% v_prcomp)

# 結果をデータフレームで表示
dot_products_df <- data.frame(
  PC = paste0("PC", 1:5),
  InnerProduct = dot_products
)
print(dot_products_df)

     PC InnerProduct
PC1 PC1            1
PC2 PC2            1
PC3 PC3           -1
PC4 PC4            1
PC5 PC5            1

全ての主成分で内積が1または-1であるため、同じ直線上の方向を指していることが確認できました。

PC3の内積が-1であるのは、スクラッチ実装の結果とprcomp()の結果でベクトルの向きがちょうど真逆であることを示しています。

3. 主成分得点の相関による確認

もし2つの主成分負荷量が等価であれば、それらを用いて計算された主成分得点の間には、完全な正の相関（相関係数=1）または完全な負の相関（相関係数=-1）が見られるはずです。

# スクラッチ実装の主成分得点
score_scratch <- principal_component_scores
# prcomp()の主成分得点
score_prcomp <- pca_result_pkg$x

# 対応する主成分得点間の相関係数を計算
correlations <- diag(cor(score_scratch, score_prcomp))

# 結果をデータフレームで表示
correlations_df <- data.frame(
  PC = paste0("PC", 1:5),
  Correlation = correlations
)
print(correlations_df)

     PC Correlation
PC1 PC1           1
PC2 PC2           1
PC3 PC3          -1
PC4 PC4           1
PC5 PC5           1

全ての主成分で相関係数が1または-1であり、両者が実質的に全く同じ情報を捉えていることがわかります。

符号が反転した固有ベクトルで計算された主成分得点は、符号も反転するため、相関係数が-1になりますが、生徒間の相対的な位置関係（誰が1位で誰が最下位かなど）の構造は完全に保たれています。

また、主成分負荷量の符号反転に伴い、対応するPC3の主成分得点の符号も反転していますが、プロットした際の相対的な位置関係は全く同じであり、解釈に影響はありません。

5. 結果の可視化

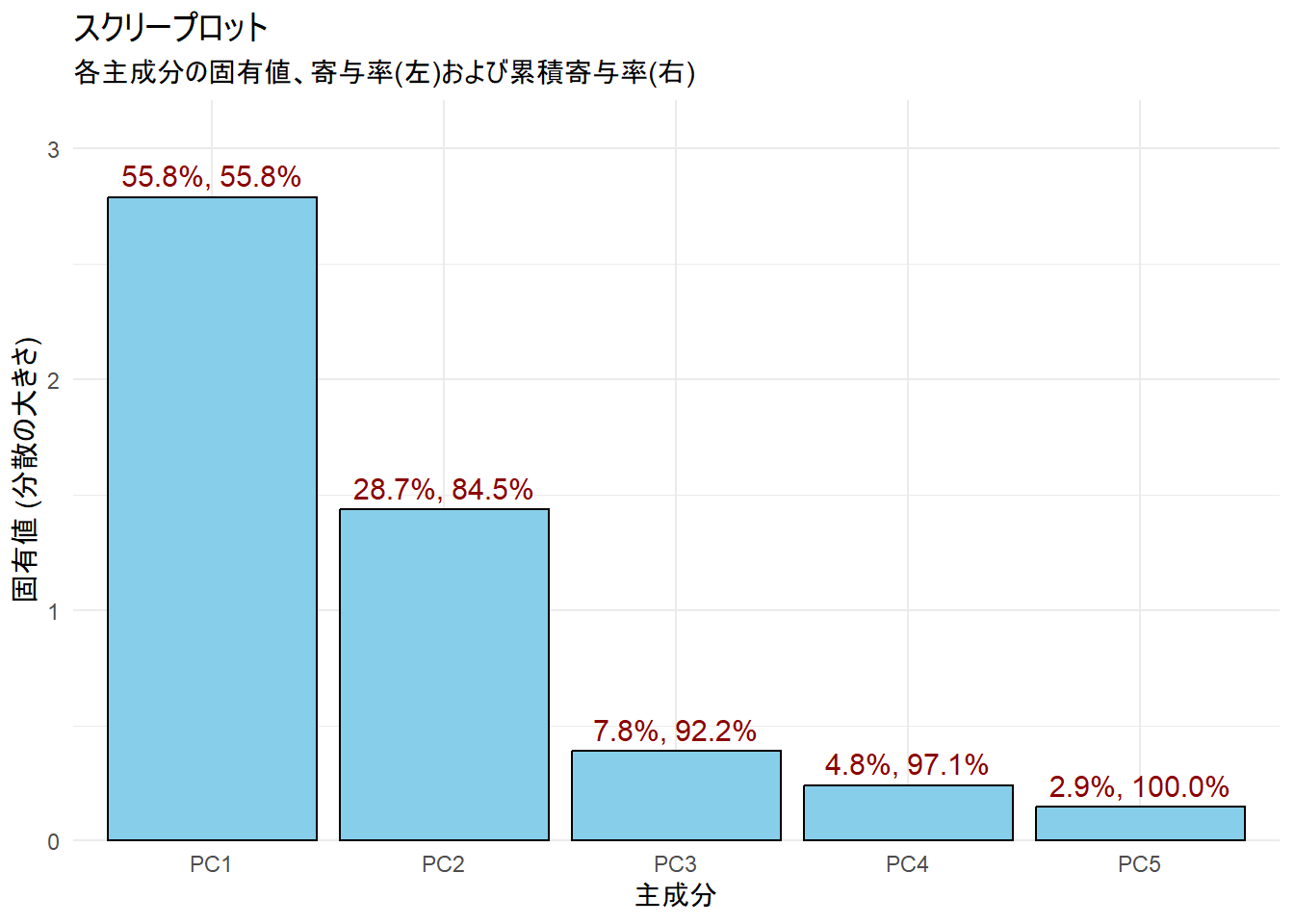
1. スクリープロット

scree_plot <- ggplot(contribution_df, aes(x = factor(PC, levels = PC))) +
  # 固有値を表す棒グラフ
  geom_bar(aes(y = Eigenvalue), stat = "identity", fill = "skyblue", color = "black") +
  # 棒グラフの上に累積寄与率をテキストで表示
  geom_text(
    aes(y = Eigenvalue, label = paste0(scales::percent(ContributionRatio, accuracy = 0.1), ", ", scales::percent(CumulativeRatio, accuracy = 0.1))),
    vjust = -0.5, # テキストを棒の上側に配置
    color = "darkred",
    size = 4
  ) +
  # Y軸の表示範囲を少し広げ、テキストが見切れないようにする
  scale_y_continuous(expand = expansion(mult = c(0, 0.15))) +
  labs(
    title = "スクリープロット",
    subtitle = "各主成分の固有値、寄与率(左)および累積寄与率(右)",
    x = "主成分",
    y = "固有値 (分散の大きさ)"
  ) +
  theme_minimal() +
  theme(legend.position = "none")

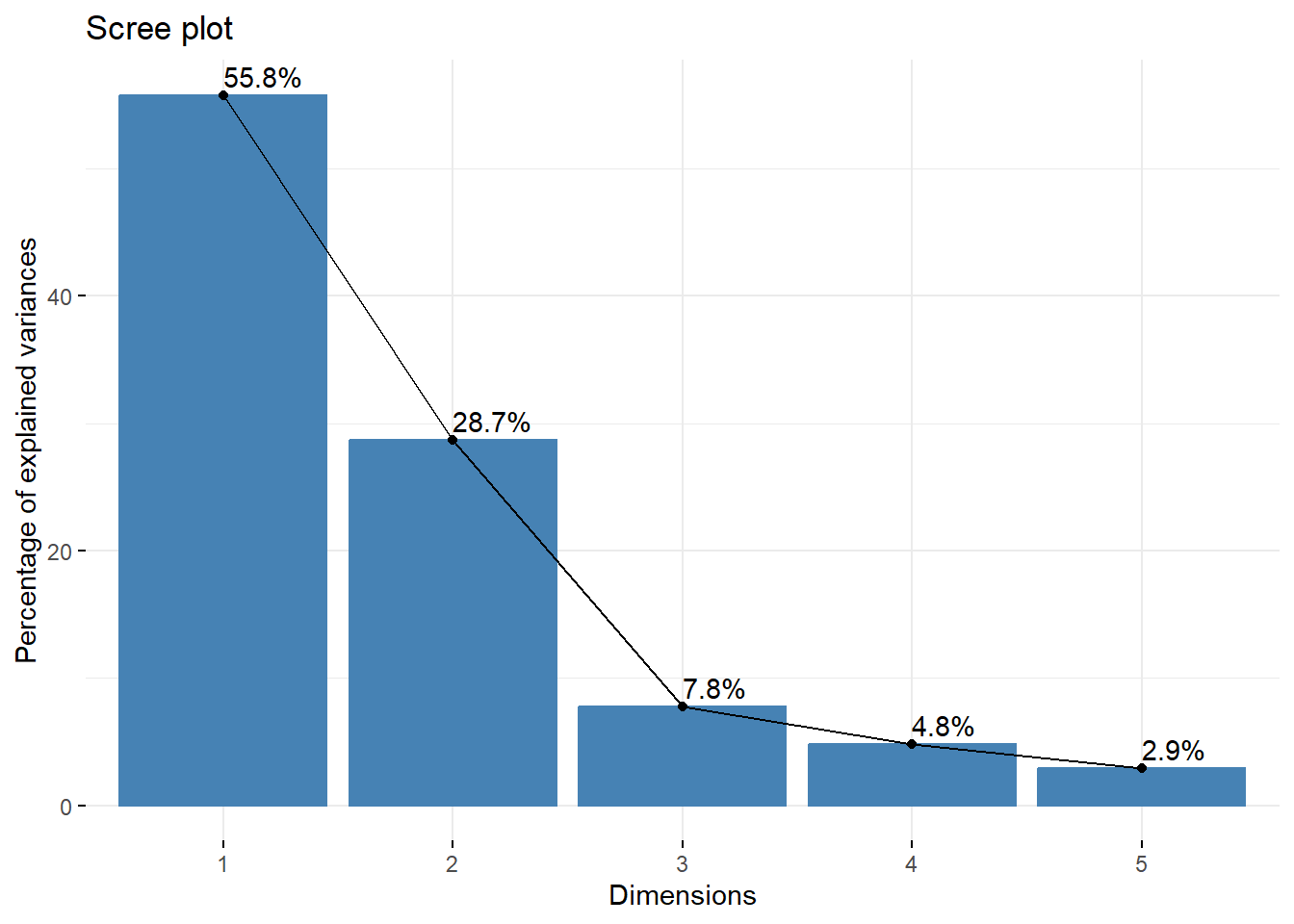
print(scree_plot)

Figure 1 は、棒グラフが各主成分の固有値（説明する分散の大きさ）を、棒の上の2つの数値はそれぞれ各主成分の寄与率と累積寄与率を示しています。

第1主成分(PC1)と第2主成分(PC2)だけで、全情報の約84.5%を説明できていることがわかります。

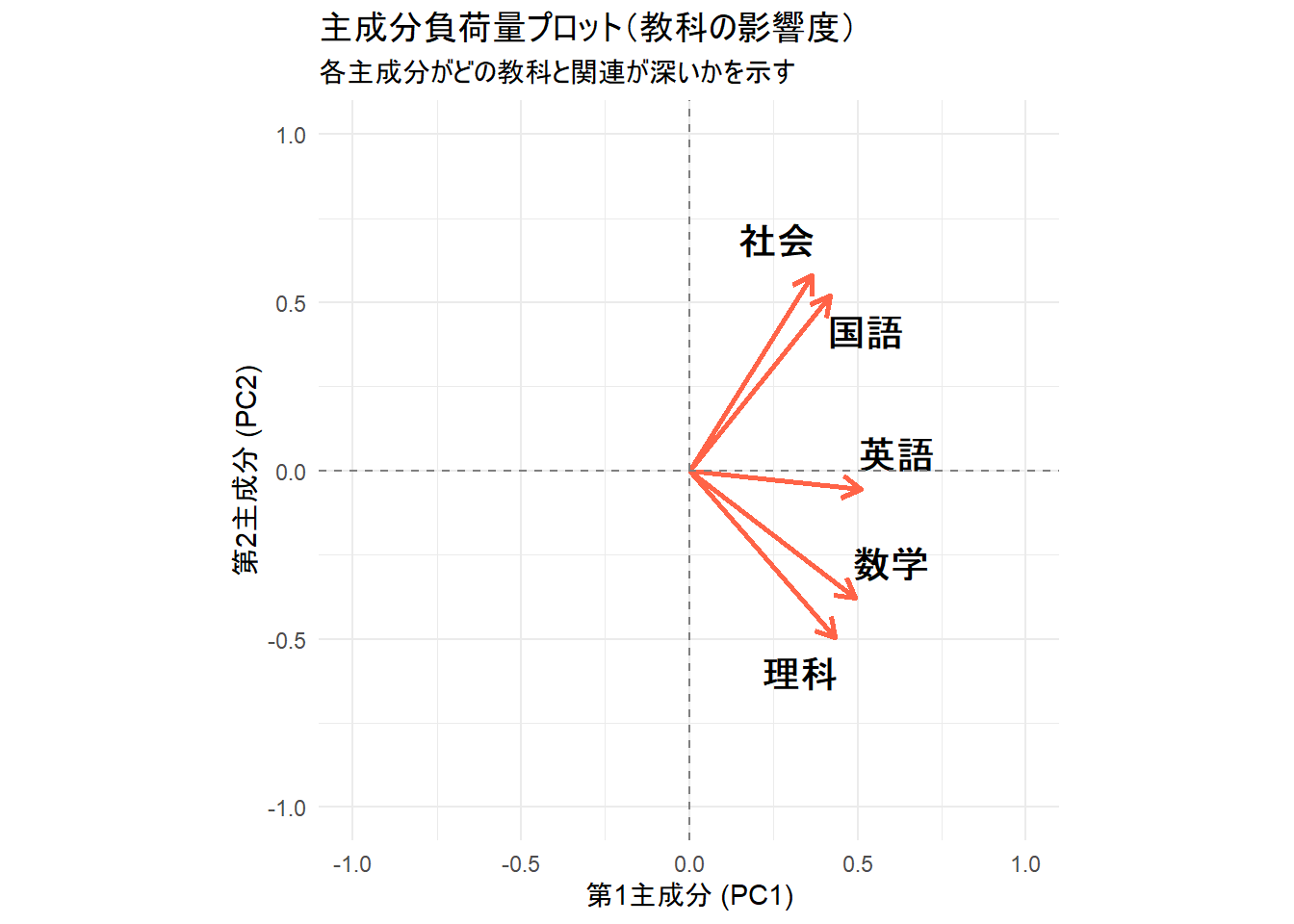
2. 主成分負荷量プロット（ローディングプロット）

loadings_df <- as.data.frame(eigen_vectors)
loadings_df$subject <- rownames(eigen_vectors)

loading_plot <- ggplot(loadings_df, aes(x = PC1, y = PC2, label = subject)) +
  # 矢印（ベクトル）を描画
  geom_segment(aes(x = 0, y = 0, xend = PC1, yend = PC2),
    arrow = arrow(length = unit(0.3, "cm")),
    color = "tomato", linewidth = 1
  ) +
  # geom_text_repel を使って教科名ラベルを表示
  ggrepel::geom_text_repel(
    size = 5,
    fontface = "bold",
    box.padding = 0.5, # テキストと矢印の先端との間の余白
    point.padding = 0.5, # テキストと他のテキストとの間の余白
    segment.color = "grey50" # テキストと点を結ぶ線の色
  ) +
  # 補助線
  geom_hline(yintercept = 0, linetype = "dashed", color = "gray50") +
  geom_vline(xintercept = 0, linetype = "dashed", color = "gray50") +
  # ラベルとタイトル
  labs(
    title = "主成分負荷量プロット（教科の影響度）",
    subtitle = "各主成分がどの教科と関連が深いかを示す",
    x = "第1主成分 (PC1)",
    y = "第2主成分 (PC2)"
  ) +
  theme_minimal() +
  # 描画範囲を固定して、円（相関円）を意識しやすくする
  coord_fixed(xlim = c(-1, 1), ylim = c(-1, 1))

print(loading_plot)

Figure 2 は、新しく作られた主成分軸（PC1, PC2）と元の5教科との関係を示しています。

第1主成分 (PC1, 横軸): 全ての教科の矢印が右側（正の方向）を向いています。これはPC1が5教科に共通する要素、すなわち「総合的な学力」を表していると解釈できます。

つまり「すべての変数が同じように増減する傾向がある」というパターンを捉えていることを意味し、学力データの文脈で言えば、

「国語ができる生徒は、数学も理科も社会も英語もできる傾向がある」
「国語が苦手な生徒は、他の教科も苦手な傾向がある」

という、全教科に共通する潜在的な能力、すなわち「総合的な学力」が、生徒たちの成績のばらつきを説明する最も大きな要因であることを示しています。

したがって、この場合のPC1は「総合学力指標」と解釈するのが自然であり、PC1の値が大きいほど、総合学力が高いことが示唆されます。

ただし、本サンプルでは全ての教科の矢印が右側（正の方向）を向いていますが、全ての矢印が左側（負の方向）を向いている場合は、PC1の値が小さい（負に大きい）ほど、総合学力が高いことが示唆される、と解釈されます。

第2主成分 (PC2, 縦軸): 「国語」、「社会」が上側（正の方向）に、「数学」、「理科」が下側（負の方向）に分かれています。これはPC2が「文系傾向 vs 理系傾向」という対立軸を表していると解釈できます。「英語」はこの軸では0に近く、文理どちらにも偏らない科目であることが示唆されます。

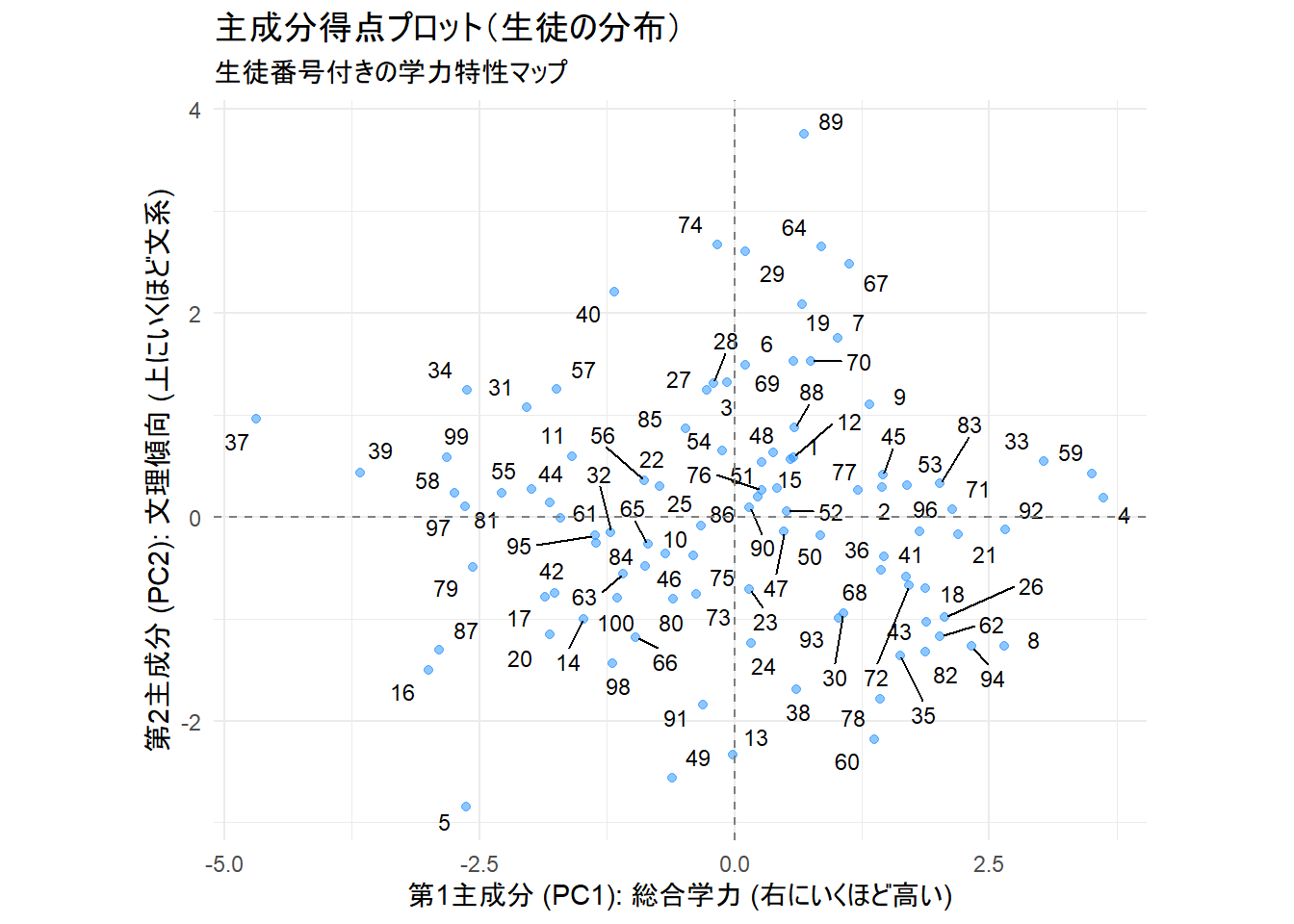
3. 主成分得点プロット（スコアプロット）

# プロット用のデータフレームを作成
scores_plot_df <- as.data.frame(principal_component_scores)
# 生徒番号(1から100)をデータフレームに追加
scores_plot_df$student_id <- 1:nrow(scores_plot_df)

score_plot <- ggplot(scores_plot_df, aes(x = PC1, y = PC2)) +
  # 生徒の位置を点でプロット
  geom_point(alpha = 0.5, color = "dodgerblue") +
  # geom_text_repel を使って生徒番号を表示
  ggrepel::geom_text_repel(
    aes(label = student_id),
    size = 3, # 文字のサイズ
    max.overlaps = 15, # ラベルの重なりを許容する最大数（調整用）
    box.padding = 0.3 # テキストと点の間の余白
  ) +
  # 補助線
  geom_hline(yintercept = 0, linetype = "dashed", color = "gray50") +
  geom_vline(xintercept = 0, linetype = "dashed", color = "gray50") +
  # ラベルとタイトル
  labs(
    title = "主成分得点プロット（生徒の分布）",
    subtitle = "生徒番号付きの学力特性マップ",
    x = "第1主成分 (PC1): 総合学力 (右にいくほど高い)",
    y = "第2主成分 (PC2): 文理傾向 (上にいくほど文系)"
  ) +
  theme_minimal() +
  coord_fixed()

print(score_plot)

Figure 3 は、100人それぞれの生徒を「総合学力(PC1)」と「文理傾向(PC2)」の2つの新しい軸で評価、マッピングしたものです。プロットの右側に位置する生徒ほど「総合学力」が高いことを示し、上側に位置する生徒ほど「文系傾向」が強く、下側に位置する生徒ほど「理系傾向」が強いことを示します。

例えば、右上の領域にいる生徒は『成績優秀な文系タイプ』、左下の領域にいる生徒は『成績はまだ伸びしろがある理系タイプ』といったように、生徒一人ひとりの学力特性を視覚的に把握することができます。

参考として Figure 3 で最も左端に位置する37番の生徒、右端に位置する4番の生徒、最も上に位置する89番の性と、そして最も下に位置する5番の生徒の成績を表示します。

scores_df[c(4, 37, 89, 5), ]

   国語 社会 数学 理科 英語
4    79   99   99  100   99
37   31   53   23   26   25
89  100   99   35   50   82
5    24   12   60   70   61

6. パッケージを利用した結果の可視化

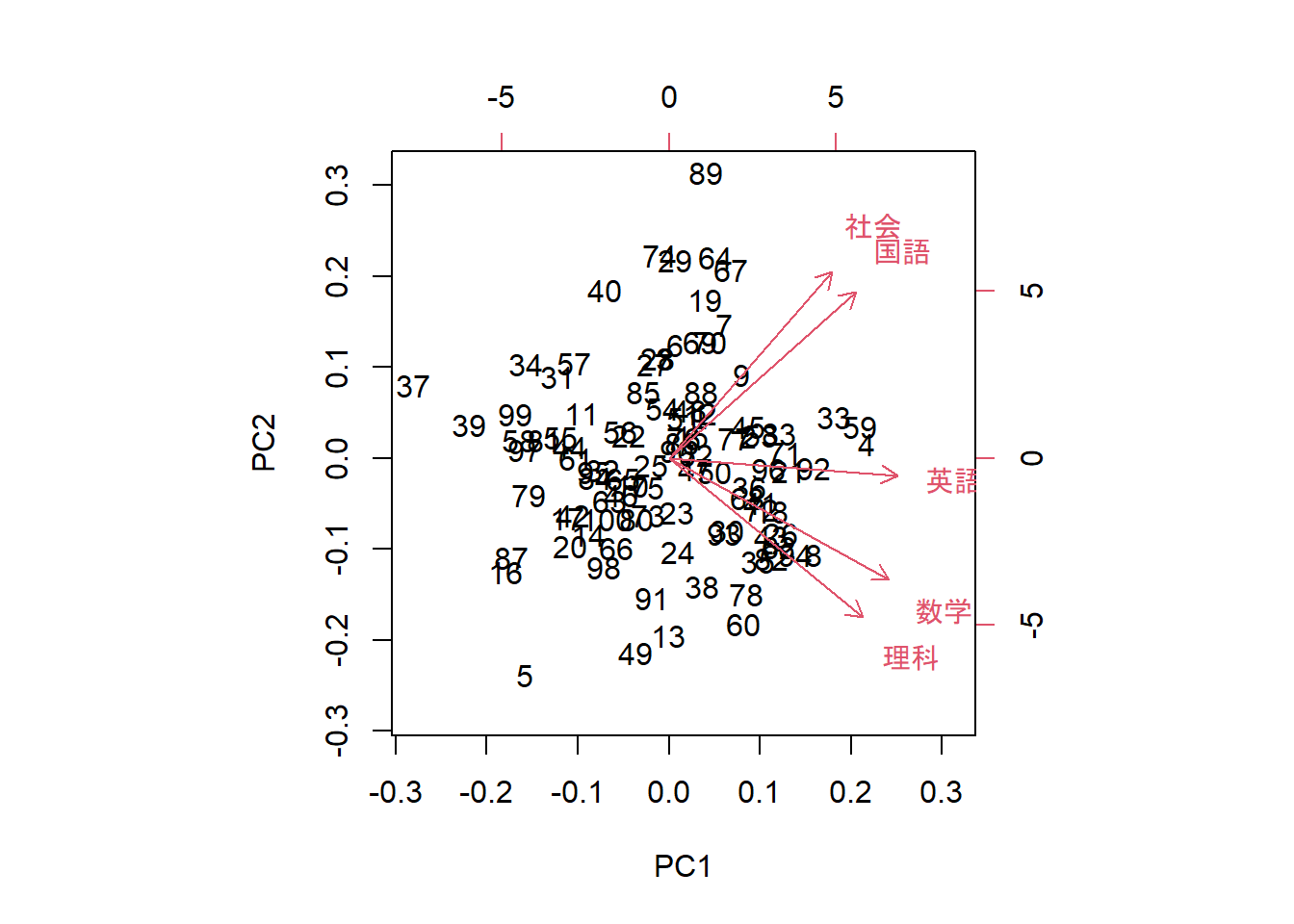
最後に、Rの関数を利用したスクリープロット、主成分得点プロットおよび主成分負荷量プロットを紹介します。

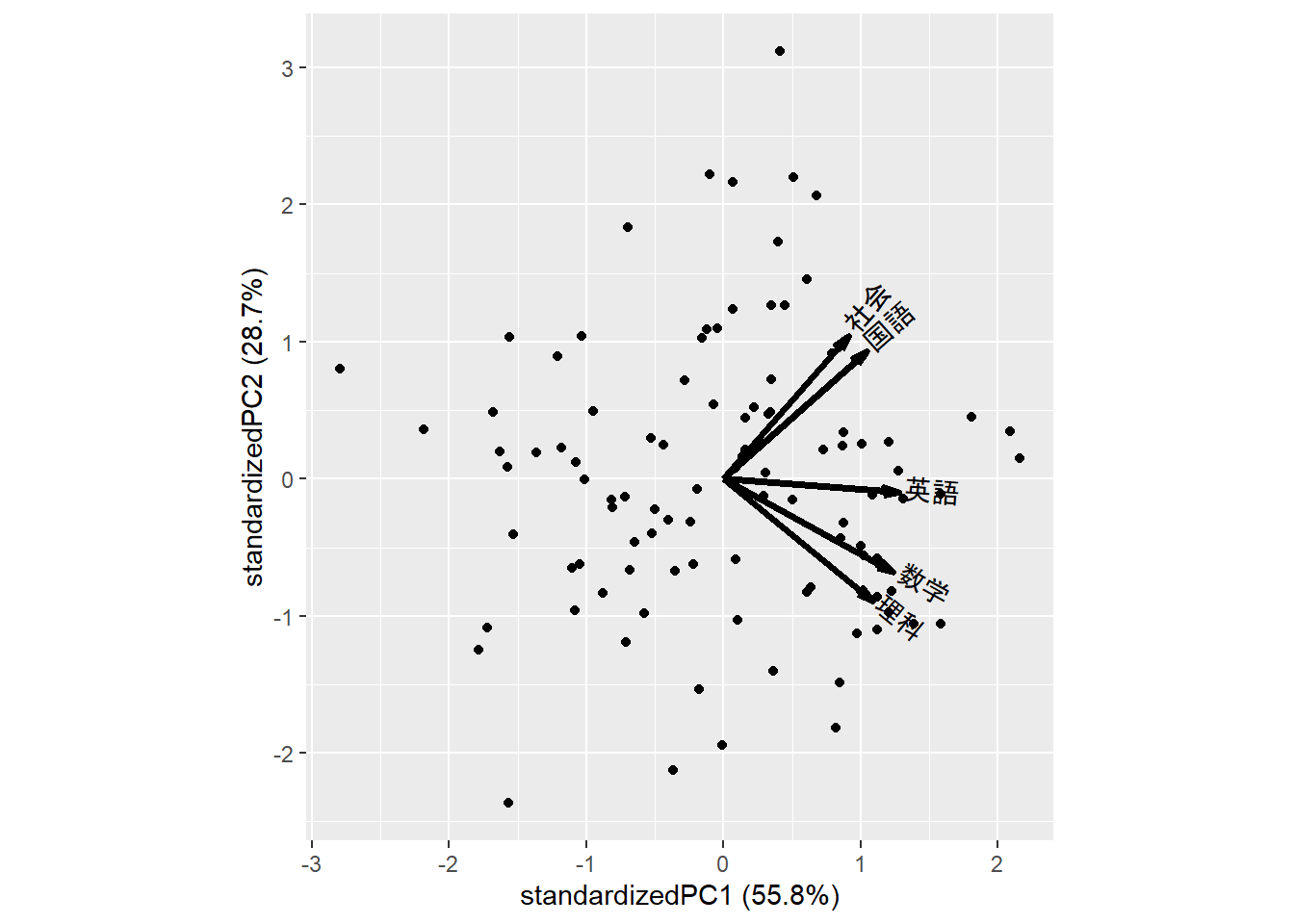
stats::biplot: Figure 4
ggbiplot::ggbiplot(): Figure 5
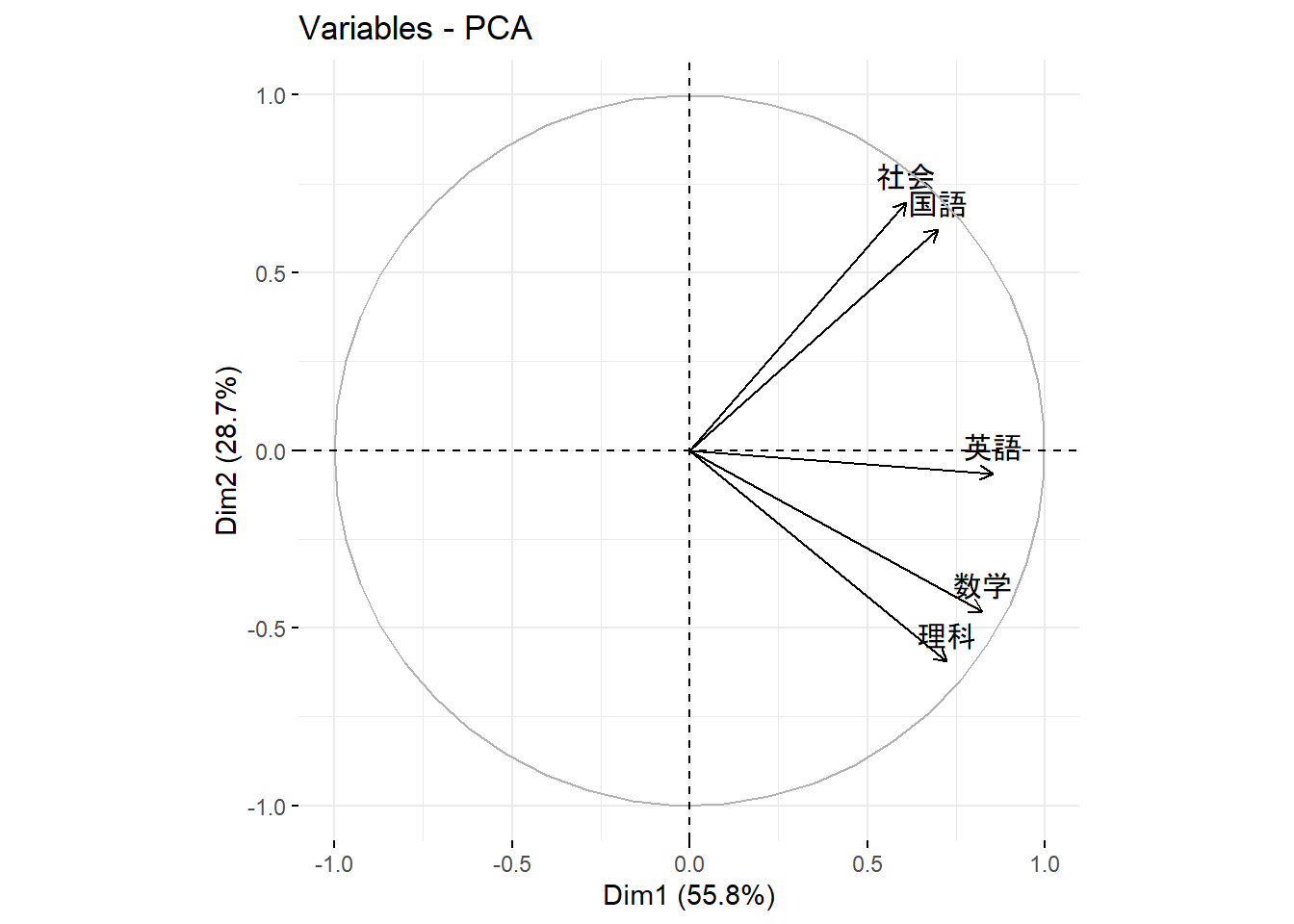
factoextra::fviz_pca_var(): Figure 6
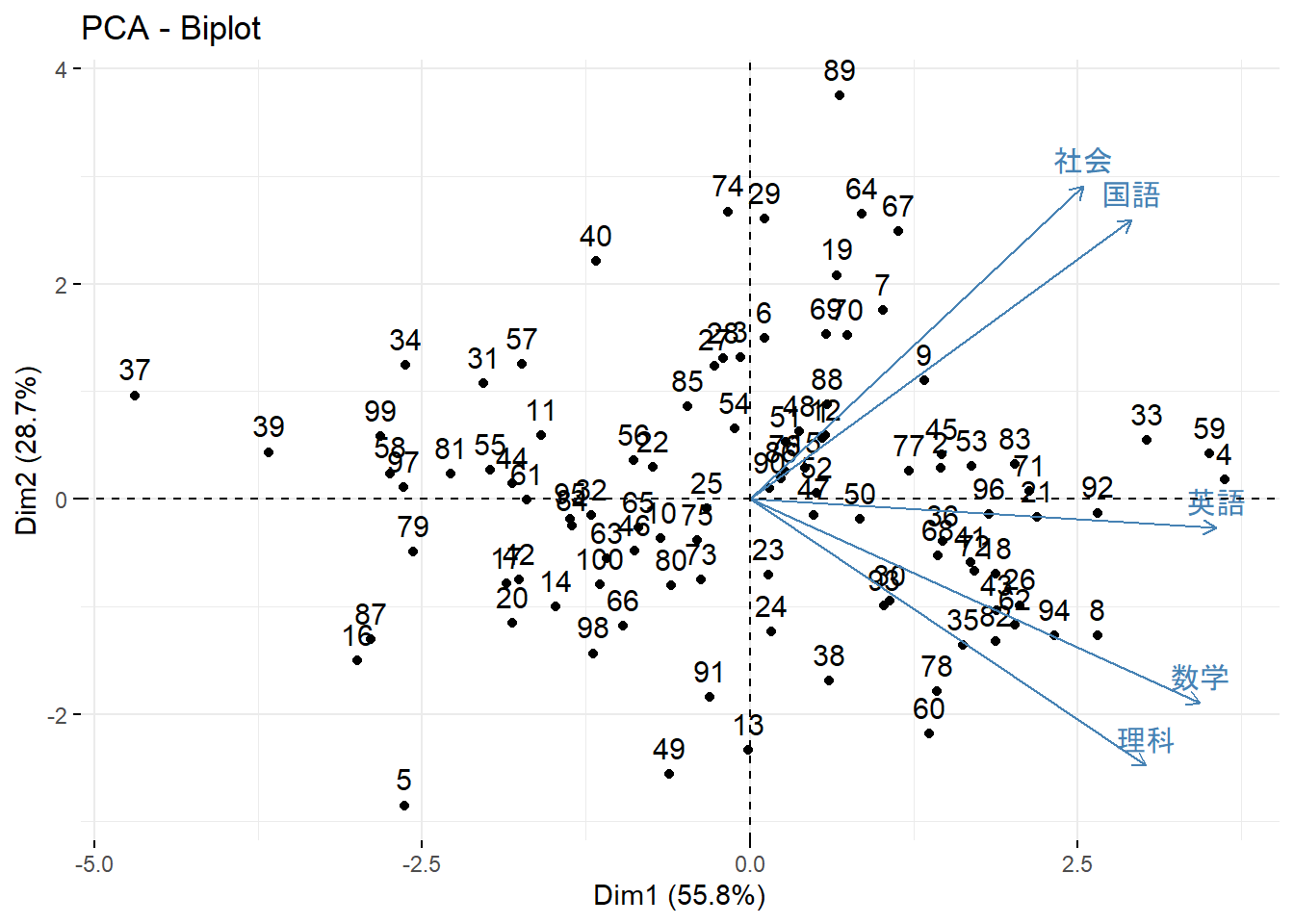
factoextra::fviz_pca_biplot(): Figure 7
factoextra::fviz_eig(): Figure 8

stats::biplot(pca_result_pkg)
ggbiplot::ggbiplot(pca_result_pkg)
factoextra::fviz_pca_var(pca_result_pkg)
factoextra::fviz_pca_biplot(pca_result_pkg)
factoextra::fviz_eig(pca_result_pkg, addlabels = TRUE)

以上です。