Rで 分散均一性検定 を試みます。
1. 分散均一性検定の解説
分散均一性検定は、2つ以上のグループ(標本)の母分散が等しいかどうかを検定する統計的手法です。
1.1. バートレット検定 (Bartlett’s Test)
バートレット検定は、複数の群の母分散が等しいという帰無仮説を検定します。
- 帰無仮説 (H₀): すべての群の母分散は等しい ( \(\sigma_1^2 = \sigma_2^2 = \dots = \sigma_k^2\) )。
- 対立仮説 (H₁): 少なくとも1つの群の母分散は他の群と異なる。
- 特徴:
- 検定統計量がカイ二乗分布に従うことを利用します。
- 重要な注意点: 標本が正規分布に従っている必要があります。正規性から逸脱しているデータに対して用いると、実際には分散が等しくても「等しくない」という誤った結果を出しやすくなります(第一種の過誤が増加する)。
1.2. コクラン検定 (Cochran’s C Test)
コクラン検定も複数の群の母分散が等しいかを検定しますが、特に最大分散が他の分散から突出している(外れている)かを検出するのに有用です。
- 帰無仮説 (H₀): すべての群の母分散は等しい ( \(\sigma_1^2 = \sigma_2^2 = \dots = \sigma_k^2\) )。
- 対立仮説 (H₁): 最大の分散を持つ群の母分散は、他の群の母分散と異なる。
- 特徴:
- 検定統計量C(C = (最大の不偏分散) / (全群の不偏分散の合計))を計算します。
- 重要な注意点: バートレット検定と同様に標本の正規性を仮定します。さらに、各群のサンプルサイズが等しい必要があります。
比較まとめ
| 特徴 | バートレット検定 | コクラン検定 |
|---|---|---|
| 目的 | 全体的な分散の等質性を検定 | 最大分散が外れ値でないかを検定 |
| 正規性の仮定 | 必要 | 必要 |
| サンプルサイズ | 異なっていても良い | 等しい必要がある |
| 感度 | 正規性から外れると影響を受けやすい | 最大分散を検出する感度が高い |
2. Rによるシミュレーション
それでは、実際にRでシミュレーションを行いましょう。 2つのシナリオを試します。
- 分散が等しい場合(帰無仮説が真): 検定が「差がない」と正しく判断するか確認します。
- 分散が異なる場合(対立仮説が真): 検定が「差がある」と正しく判断するか確認します。
なお、有意水準は5%とします。
2.1. 準備:ライブラリの読み込み
outliersはコクラン検定のcochran.test()関数を実行するために使用します。
library(ggplot2)
library(outliers)
seed <- 202507032.2. シナリオ1:分散が等しいデータ (H₀が真)
3つのグループ(A, B, C)を作成します。平均はすべて10、標準偏差もすべて2で、サンプルサイズは300とします。
データ作成
set.seed(seed)
# 各グループのサンプルサイズ
n <- 300
# 分散が等しい3つのグループを正規乱数で生成
group_a <- rnorm(n, mean = 10, sd = 2)
group_b <- rnorm(n, mean = 10, sd = 2)
group_c <- rnorm(n, mean = 10, sd = 2)
# データを扱いやすいようにデータフレームにまとめる
df_homo <- data.frame(
value = c(group_a, group_b, group_c),
group = factor(rep(c("A", "B", "C"), each = n))
)可視化 (ggplot)
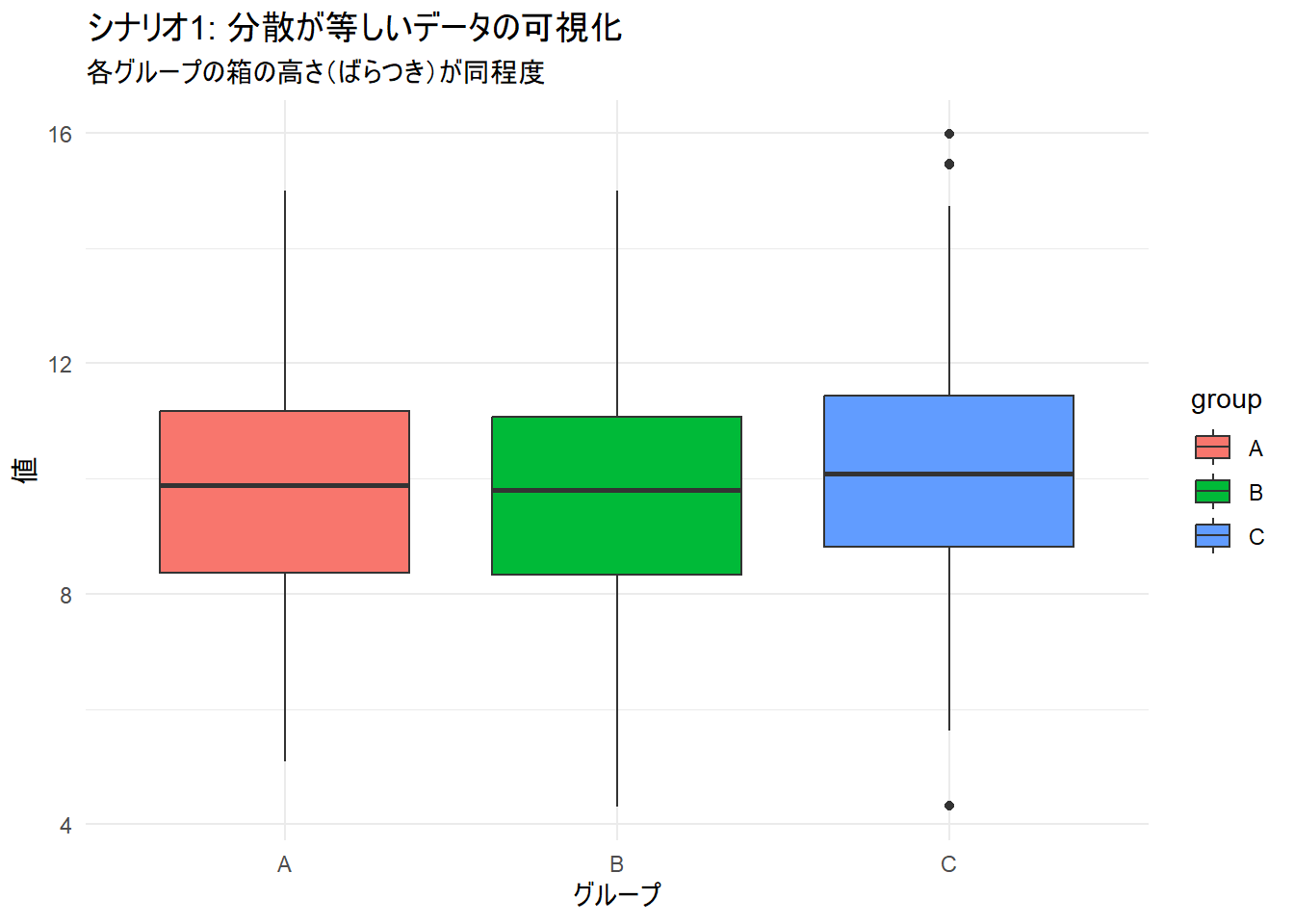
箱ひげ図でデータのばらつきを確認します。箱の高さ(四分位範囲)が各グループで同程度であることが見て取れます。
分散均一性検定の実行
バートレット検定
cat("--- バートレット検定の結果 ---\n")
bartlett.test(value ~ group, data = df_homo)--- バートレット検定の結果 ---
Bartlett test of homogeneity of variances
data: value by group
Bartlett's K-squared = 0.7538, df = 2, p-value = 0.686結果の解釈: p値が 0.686 となりました。これは設定した有意水準0.05よりも大きいため、「各群の分散は等しい」という帰無仮説を棄却できません。
コクラン検定
cat("--- コクラン検定の結果 ---\n")
cochran.test(value ~ group, data = df_homo)--- コクラン検定の結果 ---
Cochran test for outlying variance
data: value ~ group
C = 0.3526, df = 300, k = 3, p-value = 0.5779
alternative hypothesis: Group B has outlying variance
sample estimates:
A B C
3.734353 4.035253 3.674717 結果の解釈: p値が 0.5779 となりました。これも有意水準0.05より大きいため、帰無仮説を棄却できません。
シナリオ1では、両方の検定が「分散は均一である」との帰無仮説を棄却できませんでした。
2.3. シナリオ2:分散が異なるデータ (H₁が真)
次に、グループZの標準偏差だけを意図的に大きくして(sd=6)、分散が異なるデータセットを作成します。
データ作成
# グループX, Yの標準偏差は2, グループZの標準偏差は6
group_x <- rnorm(n, mean = 10, sd = 2)
group_y <- rnorm(n, mean = 10, sd = 2)
group_z <- rnorm(n, mean = 10, sd = 6) # このグループだけ分散が大きい
# データフレームにまとめる
df_hetero <- data.frame(
value = c(group_x, group_y, group_z),
group = factor(rep(c("X", "Y", "Z"), each = n))
)可視化 (ggplot)
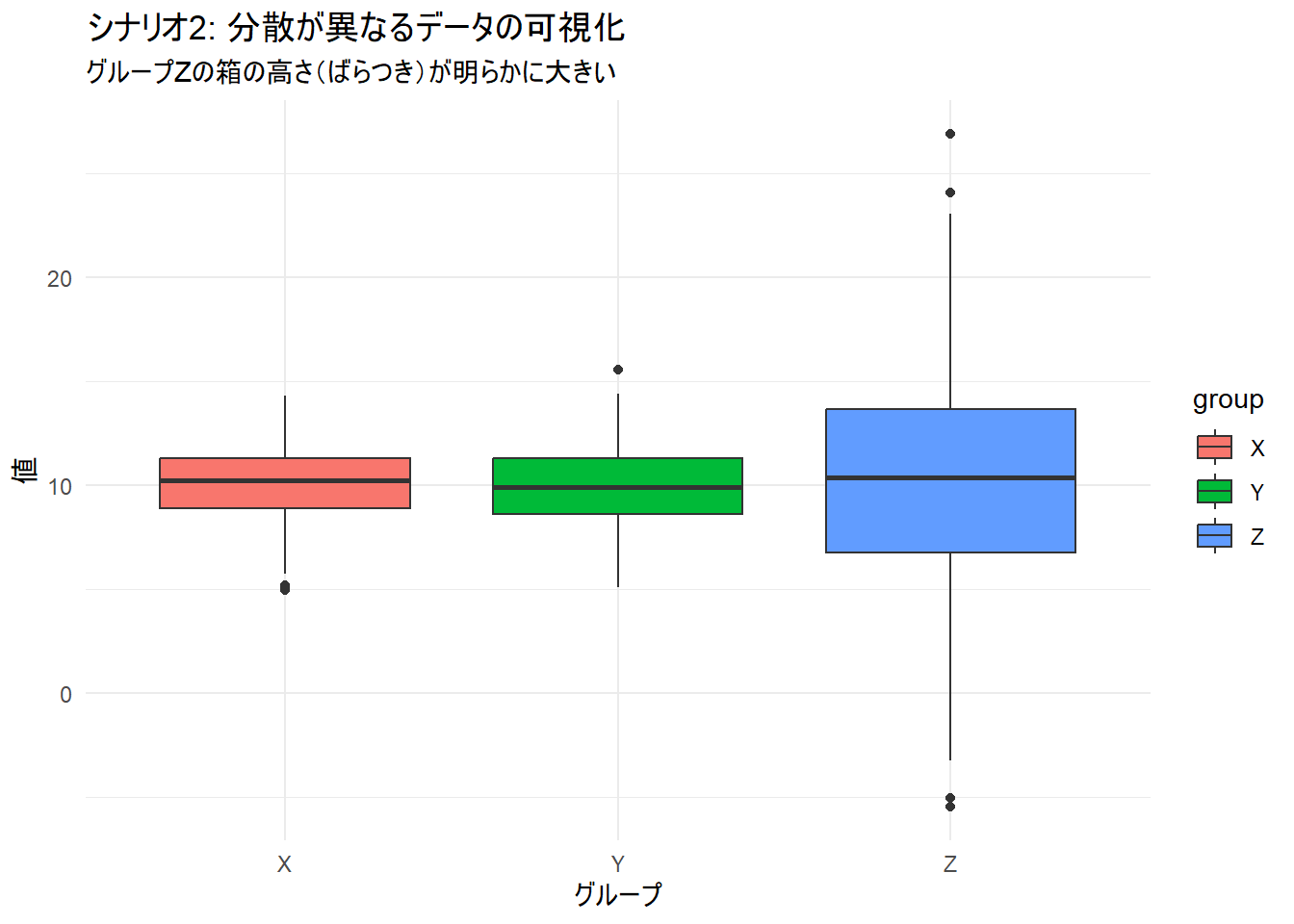
箱ひげ図を見ると、グループZの箱が他のグループより明らかに縦に長く、ばらつき(分散)が大きいことが視覚的にわかります。
分散均一性検定の実行
バートレット検定
cat("--- バートレット検定の結果 ---\n")
bartlett.test(value ~ group, data = df_hetero)--- バートレット検定の結果 ---
Bartlett test of homogeneity of variances
data: value by group
Bartlett's K-squared = 480.14, df = 2, p-value < 2.2e-16結果の解釈: p値は有意水準0.05よりも小さい < 2.2e-16となりました。したがって、「各群の分散は等しい」という帰無仮説は棄却されます。つまり、少なくとも1つの群の分散は異なると判断します。
コクラン検定
cat("--- コクラン検定の結果 ---\n")
cochran.test(value ~ group, data = df_hetero)--- コクラン検定の結果 ---
Cochran test for outlying variance
data: value ~ group
C = 0.80834, df = 300, k = 3, p-value < 2.2e-16
alternative hypothesis: Group Z has outlying variance
sample estimates:
X Y Z
3.367865 3.570424 29.263620 結果の解釈: p値が < 2.2e-16 となり、こちらも有意水準0.05より小さい結果になりました。帰無仮説は棄却され、最大の分散を持つグループZが外れ値である(分散が他と異なる)と判断します。
シナリオ2では、両方の検定が正しく「分散は均一ではない」と検出し、特にコクラン検定はどのグループが原因であるか(Group Z)を示唆してくれました。
まとめ
このシミュレーションを通じて、以下の点が確認できました。
- 分散均一性検定は、視覚的な確認(箱ひげ図など)と合わせて、グループ間の分散の等質性を客観的に評価するのに役立ちます。
- バートレット検定は全体的な分散の差を検出し、コクラン検定は特に最大の分散が突出しているかを検出するのに有用です。
- どちらの検定も、データが正規分布に従うと前提していることに注意が必要です。
- 前提条件が満たされない場合(特に正規性がない場合)は、ルビーン検定 (Levene’s Test) や フリグナー-キリーン検定 (Fligner-Killeen Test) の利用が検討されます。
以上です。