Rで 単位根検定と6つの検定統計量 を確認します。
1. 単位根検定と6つの検定統計量の解説
単位根とは?
時系列データが単位根(Unit Root)を持つとは、そのデータが非定常過程であり、過去のショック(誤差)の影響が永続的に残る性質を持つことを意味します。代表的な単位根過程はランダムウォーク (y_t = y_{t-1} + ε_t) です。単位根を持つデータに対して通常の回帰分析を行うと、変数間に本当は関係がないのに、見かけ上は有意な関係があるように見えてしまう「見せかけの回帰」という問題が発生します。
そのため、回帰分析の前にデータが定常過程か、それとも単位根過程かを確認する必要があります。そのための統計的検定が単位根検定であり、多くの場合で利用されるのがDickey-Fuller (DF)検定およびその拡張版である拡張Dickey-Fuller (ADF)検定です。
Dickey-Fuller検定の3つのモデル
DF検定では、データがどのような非定常性を持つかに応じて、以下の3つの回帰モデルを使い分けます。
- モデル1: 定数項なし、トレンドなし (None)
Δy_t = γ * y_{t-1} + ε_t- 純粋なランダムウォークを想定したモデルです。
- モデル2: 定数項あり、トレンドなし (Drift)
Δy_t = μ + γ * y_{t-1} + ε_t- ドリフト付きランダムウォーク(一定の方向に流れていく傾向)を想定したモデルです。
- モデル3: 定数項あり、トレンドあり (Trend)
Δy_t = μ + β*t + γ * y_{t-1} + ε_t- 時間トレンドの周りをランダムウォークする過程を想定したモデルです。
これらのモデルにおいて、検定の核心は係数 γ が0であるかどうかを調べることです。
- 帰無仮説 H₀:
γ = 0→ 単位根が存在する(非定常) - 対立仮説 H₁:
γ < 0→ 単位根は存在しない(定常またはトレンド定常)
6つの検定統計量
これらのモデルと帰無仮説の組み合わせから、以下の6つの主要な検定統計量が導出されます。これらの統計量の分布は、一般的なt分布やF分布とは異なるDickey-Fuller分布に従うため、専用の臨界値を用いて検定を行います。
| 検定モデル | 回帰式 | 検定統計量 | 帰無仮説 (H₀) | 対立仮説 (H₁) | R(urca)でのType |
|---|---|---|---|---|---|
| モデル1 | Δy_t = γ * y_{t-1} + ε_t | tau1 (τ₁) | γ = 0 (単位根あり) | γ < 0 (定常) | none |
| モデル2 | Δy_t = μ + γ * y_{t-1} + ε_t | tau2 (τ₂) | γ = 0 (単位根あり) | γ < 0 (定常) | drift |
phi1 (Φ₁) | γ = 0 and μ = 0 (ドリフトなし単位根) | H₀でない | drift | ||
| モデル3 | Δy_t = μ + β*t + γ * y_{t-1} + ε_t | tau3 (τ₃) | γ = 0 (単位根あり) | γ < 0 (トレンド定常) | trend |
phi2 (Φ₂) | γ = 0 and μ=0 and β = 0 (純粋なランダムウォーク) | H₀でない | trend | ||
phi3 (Φ₃) | γ = 0 and β = 0 (トレンドなし単位根) | H₀でない | trend |
- tau (τ) 統計量:
γの係数が0であるという仮説を検定するための、t検定統計量に似た統計量です。 - phi (Φ) 統計量:
γや定数項μ、トレンド項βの係数が同時に0であるという複合仮説を検定するための、F検定統計量に似た統計量です。
2. Rによるシミュレーション
それでは、実際にRを用いてシミュレーションを行い、これらの統計量がどのような分布を示すかを確認します。
2.1. 準備
まず、シミュレーションと可視化に必要なライブラリを読み込みます。
# ライブラリの読み込み
library(urca)
library(ggplot2)
library(dplyr)
library(tidyr)
result_output <- "D:/result_output"2.2. サンプルデータの作成と可視化
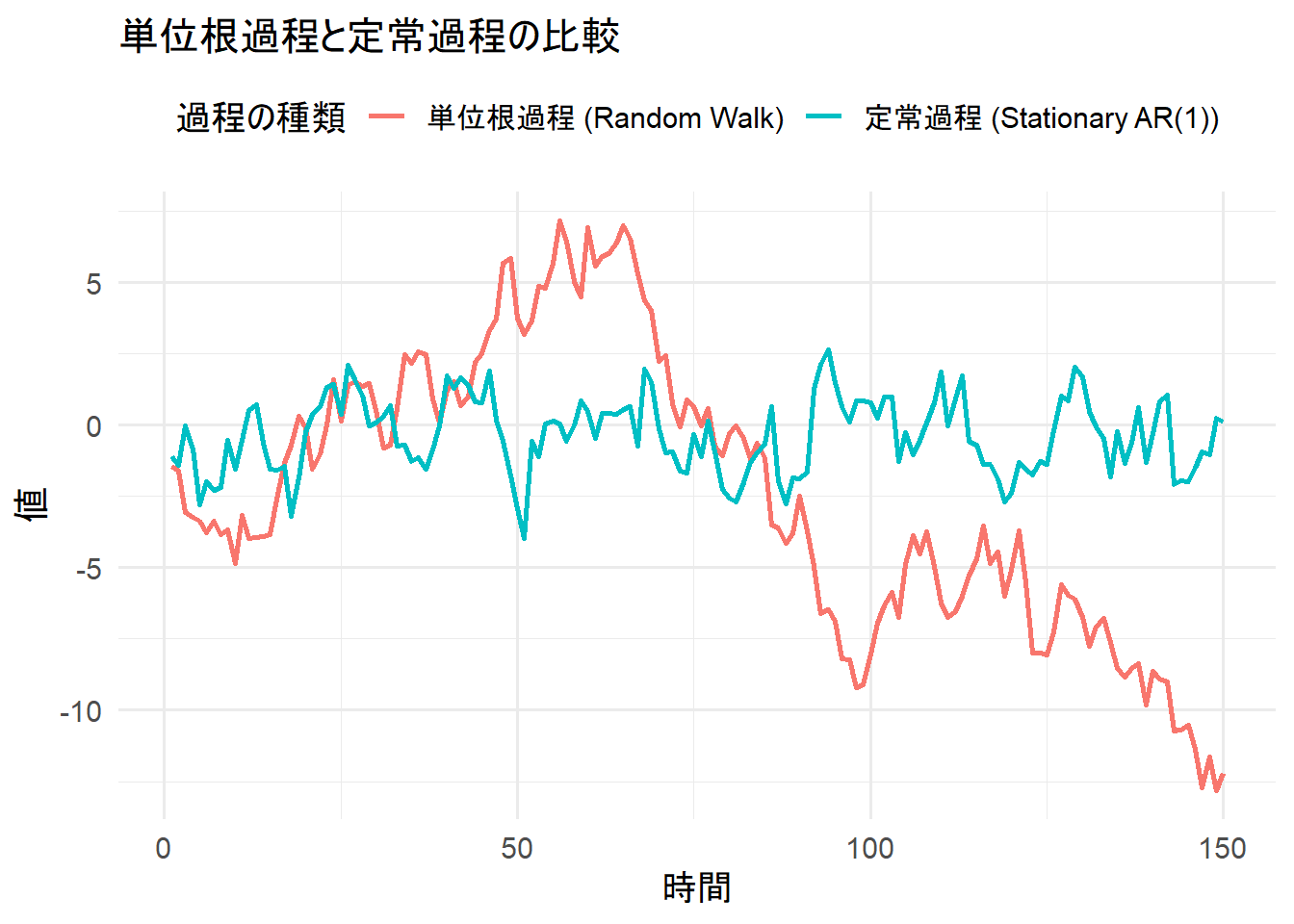
単位根過程(ランダムウォーク)と定常過程(AR(1)モデル)のデータを生成し、その違いを視覚的に確認します。
seed <- 20250703
set.seed(seed)
n_obs <- 150
# 単位根過程 (ランダムウォーク)
random_walk <- cumsum(rnorm(n_obs))
# 定常過程 (AR(1)モデル, ρ=0.7)
stationary_ar1 <- arima.sim(model = list(ar = 0.7), n = n_obs)
# データフレームに整形
df_sample <- data.frame(
time = 1:n_obs,
`単位根過程 (Random Walk)` = random_walk,
`定常過程 (Stationary AR(1))` = stationary_ar1, check.names = F
) %>%
pivot_longer(cols = -time, names_to = "process_type", values_to = "value")
# ggplotでプロット
ggplot(df_sample, aes(x = time, y = value, color = process_type)) +
geom_line(linewidth = 1) +
labs(
title = "単位根過程と定常過程の比較",
x = "時間",
y = "値",
color = "過程の種類"
) +
theme_minimal(base_size = 14) +
theme(legend.position = "top")プロットから、定常過程は平均値の周りを変動しているのに対し、単位根過程は特定の平均値に戻る傾向がなく、不規則に変動し続ける様子がわかります。
2.3. シミュレーションの実行
帰無仮説(データが単位根過程である)が真の場合、6つの検定統計量がどのような分布になるかをシミュレーションで確認します。ランダムウォークデータを多数生成し、それぞれに対してDF検定を実行して統計量を収集します。
set.seed(seed)
# シミュレーションの設定
n_sim <- 2000 # シミュレーション回数
n_obs <- 100 # 各時系列の長さ
# 結果を格納するデータフレームを初期化
results <- tibble(
sim_id = 1:n_sim,
tau1 = numeric(n_sim),
tau2 = numeric(n_sim),
phi1 = numeric(n_sim),
tau3 = numeric(n_sim),
phi2 = numeric(n_sim),
phi3 = numeric(n_sim)
)
# シミュレーションループ
for (i in 1:n_sim) {
# 帰無仮説が真となるデータ (ランダムウォーク) を生成
y <- cumsum(rnorm(n_obs))
# type = "none" の検定 (tau1)
res_none <- ur.df(y, type = "none", lags = 0)
results$tau1[i] <- res_none@teststat[1, 1]
# type = "drift" の検定 (tau2, phi1)
res_drift <- ur.df(y, type = "drift", lags = 0)
results$tau2[i] <- res_drift@teststat[1, 1]
results$phi1[i] <- res_drift@teststat[1, 2]
# type = "trend" の検定 (tau3, phi2, phi3)
res_trend <- ur.df(y, type = "trend", lags = 0)
results$tau3[i] <- res_trend@teststat[1, 1]
results$phi2[i] <- res_trend@teststat[1, 2]
results$phi3[i] <- res_trend@teststat[1, 3]
}
# tbl オブジェクトの保存
setwd(result_output)
saveRDS(object = results, file = "unit_root.rds")2.4. シミュレーション結果の可視化と考察
シミュレーションで得られた2000個の検定統計量の分布をヒストグラムで可視化します。また、urcaパッケージから取得できる5%水準の臨界値(Critical Value)を破線で追加し、棄却域との関係を見ます。
set.seed(seed)
# tbl オブジェクトの読み込み
setwd(result_output)
results <- readRDS("unit_root.rds")
# 臨界値を取得 (urcaパッケージのsummaryオブジェクトから)
y_dummy <- cumsum(rnorm(100)) # 臨界値取得用のダミーデータ
summary_none <- summary(ur.df(y_dummy, type = "none", lags = 0))
summary_drift <- summary(ur.df(y_dummy, type = "drift", lags = 0))
summary_trend <- summary(ur.df(y_dummy, type = "trend", lags = 0))
cvals_df <- tibble(
statistic = factor(c("tau1", "tau2", "phi1", "tau3", "phi2", "phi3"),
levels = c("tau1", "tau2", "tau3", "phi1", "phi2", "phi3")
),
critical_value = c(
summary_none@cval[1, "5pct"], # tau1
summary_drift@cval["tau2", "5pct"], # tau2
summary_drift@cval["phi1", "5pct"], # phi1
summary_trend@cval["tau3", "5pct"], # tau3
summary_trend@cval["phi2", "5pct"], # phi2
summary_trend@cval["phi3", "5pct"] # phi3
)
)
# プロット用にデータを整形
results_long <- results %>%
select(-sim_id) %>%
pivot_longer(everything(), names_to = "statistic", values_to = "value") %>%
mutate(statistic = factor(statistic, levels = c("tau1", "tau2", "tau3", "phi1", "phi2", "phi3")))
# ggplotで分布をプロット
ggplot(results_long, aes(x = value)) +
geom_histogram(aes(y = ..density..), bins = 50, fill = "skyblue", color = "black", alpha = 0.7) +
geom_density(color = "red", linewidth = 1) +
# 臨界値を垂線として追加
geom_vline(
data = cvals_df, aes(xintercept = critical_value),
color = "blue", linetype = "dashed", linewidth = 1.2
) +
facet_wrap(~statistic, scales = "free", ncol = 3) +
labs(
title = "単位根過程における各検定統計量の分布(シミュレーション結果)",
subtitle = "青い破線は5%棄却臨界値。検定統計量がこの線より左(tau)または右(phi)にあれば帰無仮説は棄却される。",
x = "検定統計量の値",
y = "密度"
) +
theme_bw(base_size = 12)考察
- tau (τ) 統計量 (τ₁, τ₂, τ₃):
- これらの分布は0より左側に偏っています。
- 検定は片側検定で行われ、検定統計量が臨界値(青い破線)よりも左側にあれば、単位根の帰無仮説は棄却されます。
- 今回のシミュレーションでは帰無仮説が真(単位根を持つ)のデータを生成したため、ほとんどの統計量は臨界値よりも右側に分布しており、正しく「帰無仮説を棄却できない」と判断されることがわかります。5%水準の検定なので、約5%の試行では誤って棄却されます(第一種の過誤)。
- phi (Φ) 統計量 (Φ₁, Φ₂, Φ₃):
- これらの分布は正規分布やt分布とは明らかに異なり、右に裾の長い形状をしています。
- 検定はF検定のように、検定統計量が臨界値よりも右側にあれば帰無仮説を棄却します。
- こちらも、ほとんどの統計量は臨界値より左側にあり、複合仮説(例:
γ=0かつβ=0)が棄却されないことがわかります。
3. まとめ
本シミュレーションを通じて、以下の点が明らかになりました。
- 単位根検定の統計量は特殊な分布に従う: DF検定の統計量は、標準的な分布に従わないため、専用の臨界値が必要です。
- モデル選択の重要性: データが従う過程(定数項やトレンドの有無)に応じて、適切な検定モデル(
none,drift,trend)を選択し、対応する検定統計量(tau1,tau2,tau3など)を解釈する必要があります。
以上です。