Rで微分方程式:1階偏微分方程式

# --- シミュレーションパラメータ ---
L <- 10.0 # 空間領域の長さ (0 <= x <= L)
Nx <- 200 # 空間の分割数
dx <- L / Nx # 空間ステップ幅
c_speed <- 1.0 # 移流速度
T_end <- 8.0 # シミュレーション終了時間
CFL <- 0.5 # クーラン数（安定性のためのパラメータ）
dt <- CFL * dx / c_speed # 時間ステップ幅

# --- 初期条件とグリッドの設定 ---
# 空間グリッド (x座標)
x <- seq(0, L, by = dx)

# 初期分布 u(t=0, x) をガウス分布（山形）で作成
u_initial <- exp(-(x - L / 4)^2 / 0.5)
u <- u_initial # uを現在の状態として保持

# 時間ステップの数
nsteps <- round(T_end / dt)

# 結果を保存するためのデータフレームを準備
results_df <- data.frame()

# シミュレーションの条件を表示
cat("--- シミュレーション条件 ---\n\n")
cat("モデル: 1次元移流方程式（1階偏微分方程式）\n")
cat(sprintf("移流速度: c = %.2f\n", c_speed))
cat(sprintf("空間: 0~%.1f, 時間: 0~%.1f\n", L, T_end))
cat("境界条件: 周期境界条件\n")
cat("--------------------------\n")

for (n in 0:nsteps) {
  # 現在のステップの結果をデータフレームに追加
  current_step_df <- data.frame(time = n * dt, x = x, u = u)
  results_df <- rbind(results_df, current_step_df)

  # uの値を次の時間ステップのためにコピー
  u_old <- u

  # 空間方向のループ（各点で次の時間ステップの値を計算）
  for (i in 2:Nx) {
    # 風上差分法による更新式
    # c > 0 なので、風上は左側(i-1)
    u[i] <- u_old[i] - (c_speed * dt / dx) * (u_old[i] - u_old[i - 1])
  }

  # 周期境界条件の適用
  # 左端(i=1)の更新
  u[1] <- u_old[1] - (c_speed * dt / dx) * (u_old[1] - u_old[Nx])

  # 右端(i=Nx+1)の値を左端と同じにする
  u[Nx + 1] <- u[1]
}

# ggplotでアニメーションを作成
p_anim <- ggplot(results_df, aes(x = x, y = u, group = 1)) +
  geom_line(color = "tomato", linewidth = 1.2) +
  scale_x_continuous(breaks = seq(0, L, by = 2)) +
  labs(
    title = "移流方程式のシミュレーション",
    subtitle = "時刻: {round(frame_time, 2)}",
    x = "位置 (x)",
    y = "濃度 (u)",
    caption = "風上差分法による数値シミュレーション結果"
  ) +
  ylim(0, 1.2) + # y軸の範囲を固定
  theme_minimal() +
  theme(
    plot.title = element_text(face = "bold", size = 28),
    plot.subtitle = element_text(size = 26),
    axis.title = element_text(size = 26),
    plot.caption = element_text(size = 26),
    axis.text.x = element_text(size = 26, color = "black"),
    axis.text.y = element_text(size = 26, color = "black")
  ) +
  # gganimateの設定
  transition_time(time) +
  ease_aes("linear")

# アニメーションをレンダリングして表示・保存
# nframesを調整するとアニメーションの長さを変更できます
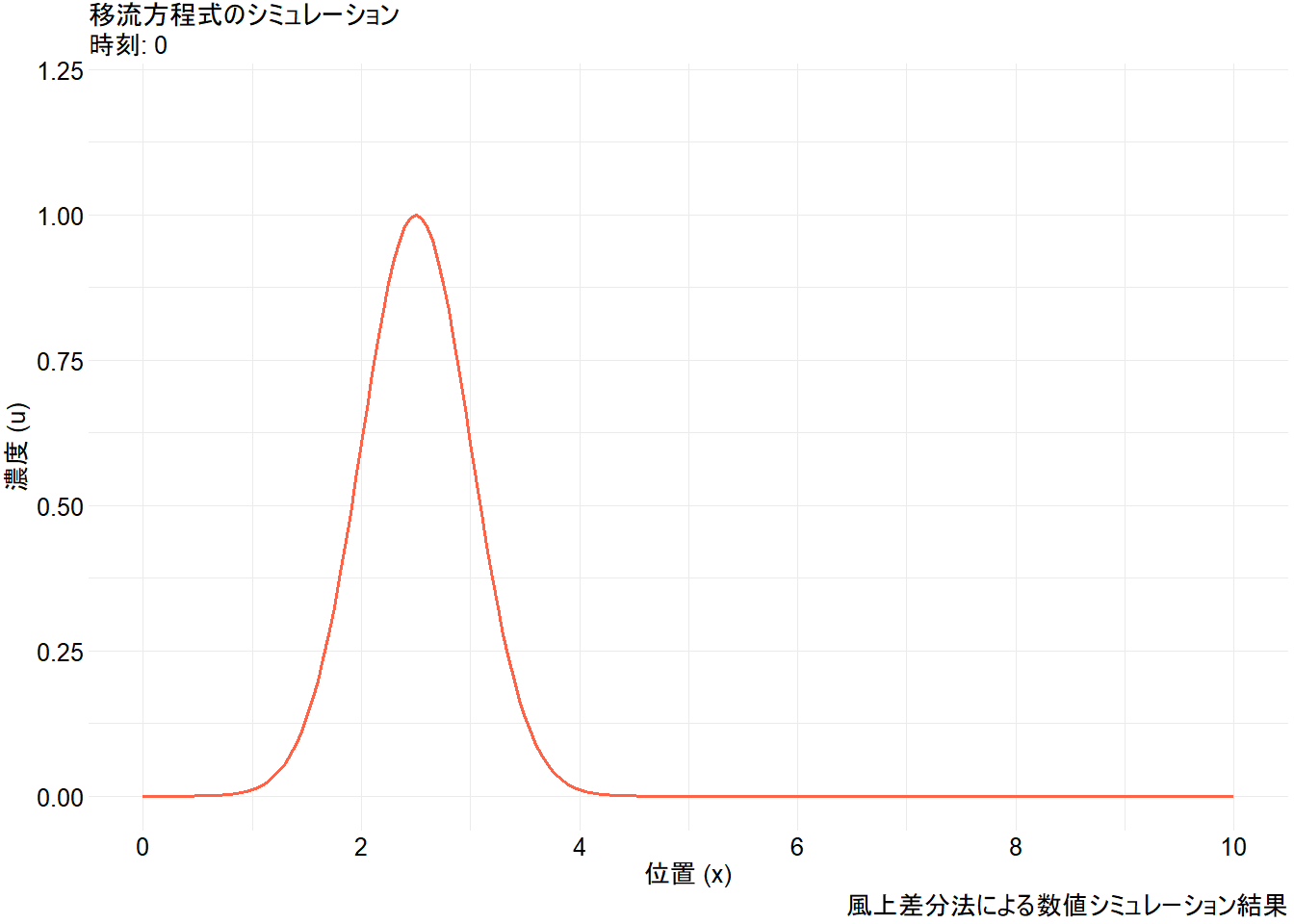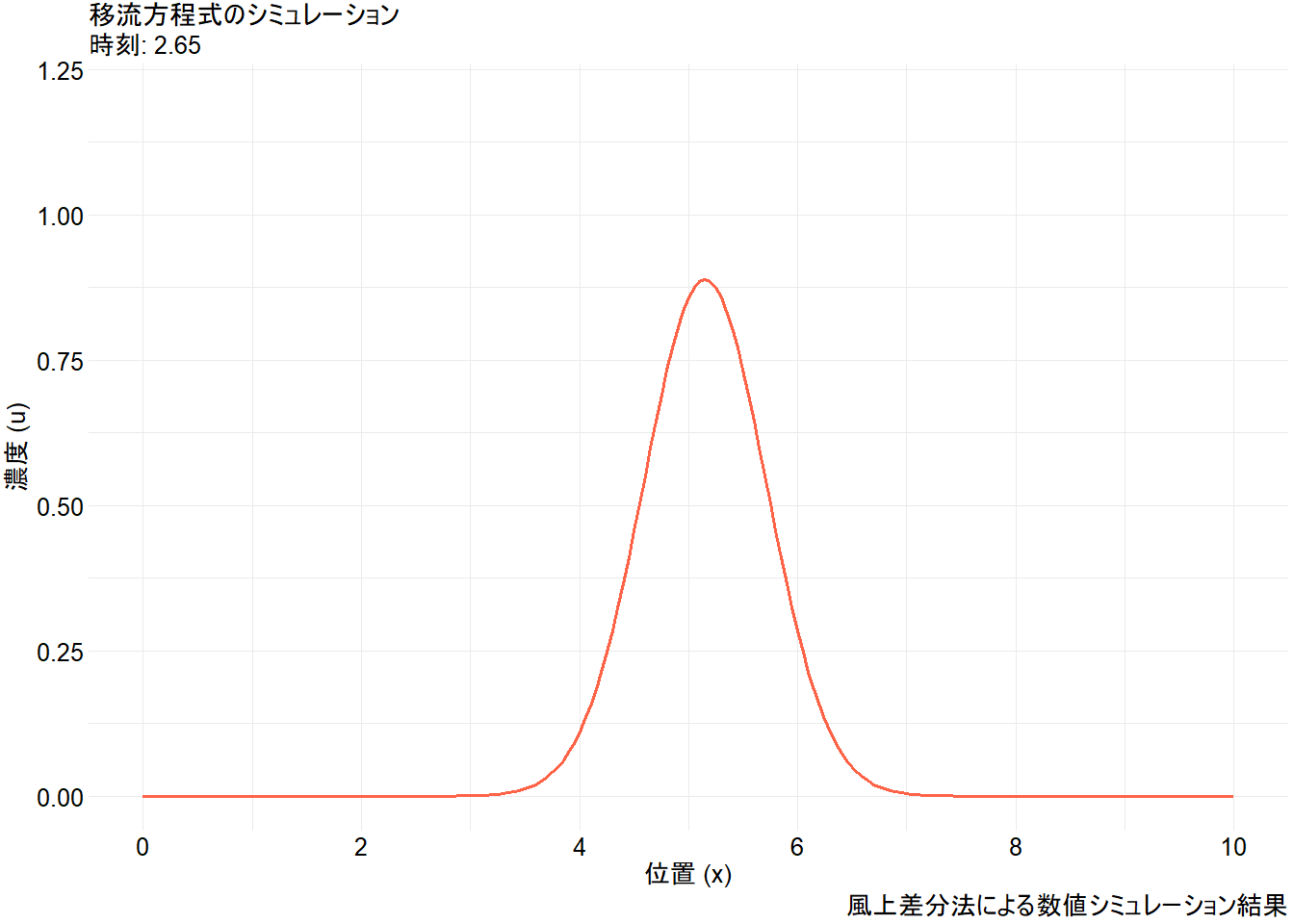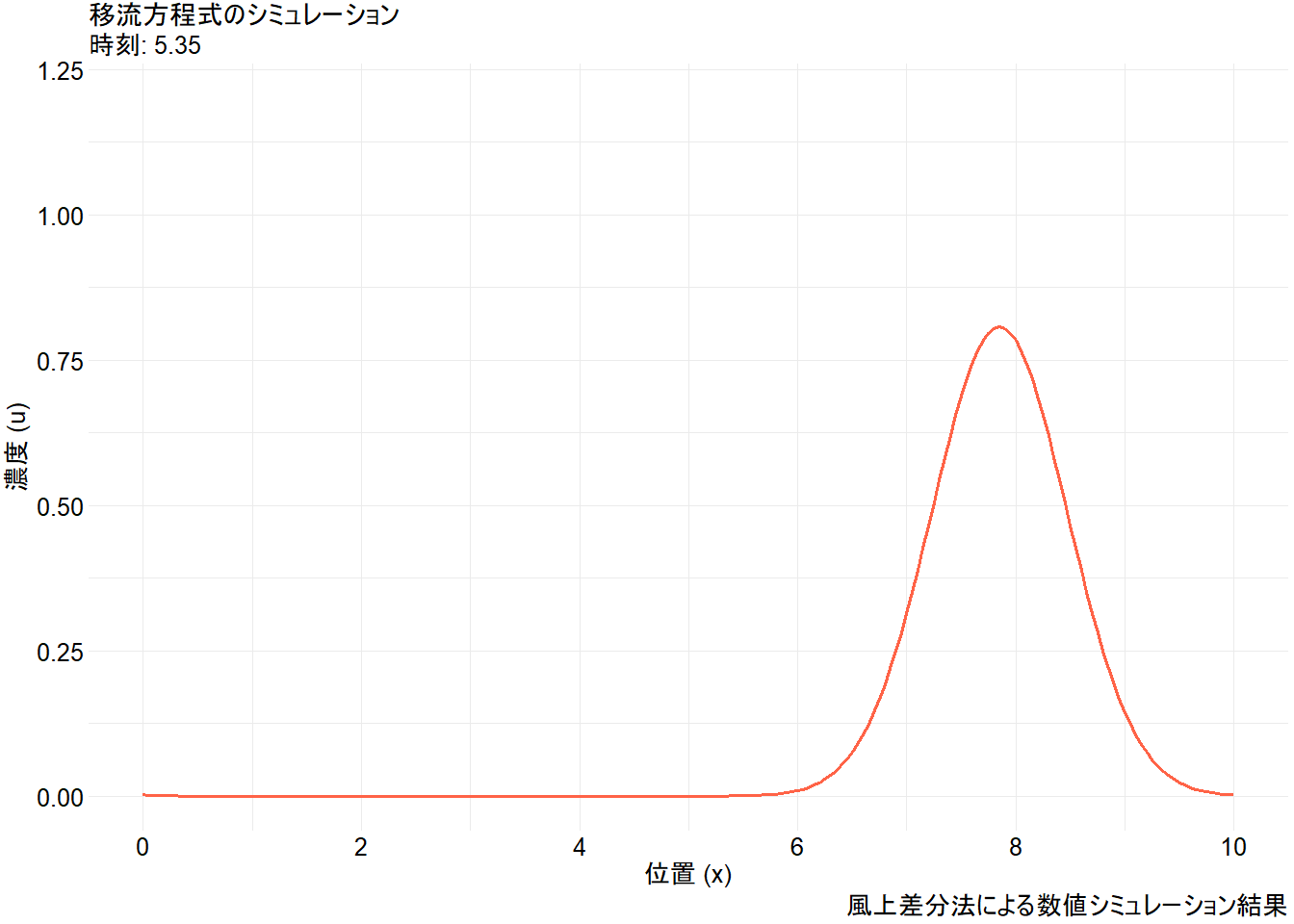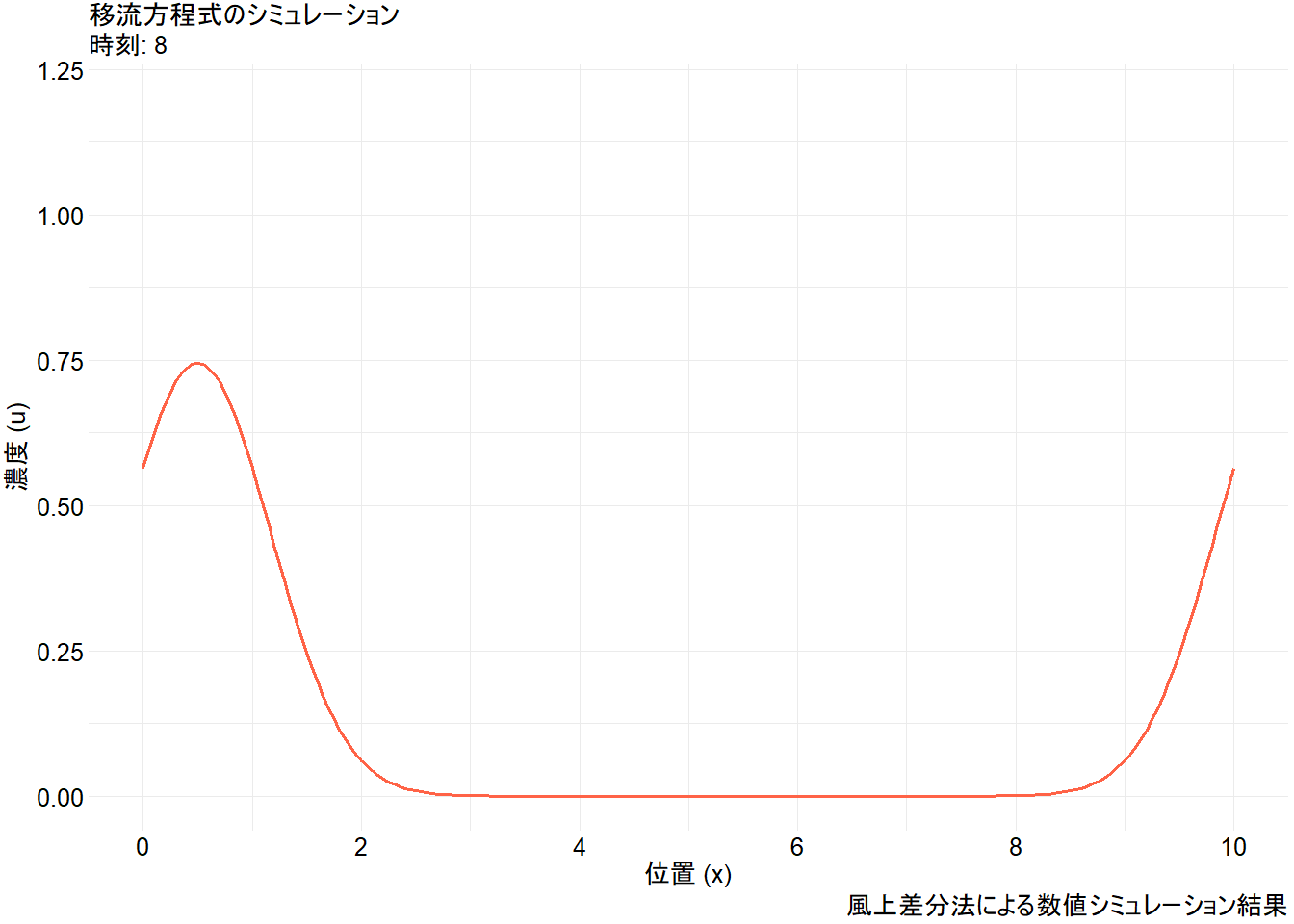
animate(p_anim, nframes = 200, fps = 20, width = 1344, height = 960, renderer = gifski_renderer("advection_simulation.gif"))