Rで 最小二乗推定量の不偏性と一致性 を確認します。
1. 最小二乗推定量(OLS)が不偏性を持つための条件
最小二乗推定量が不偏推定量(推定量の期待値が真の値と等しくなる性質)であるためには、いくつかの「ガウス=マルコフの仮定」を満たす必要があります。その中で、不偏性のために特に重要なのは以下の4つです。
- 線形性: モデルがパラメータについて線形である。
- ランダムサンプリング: データが母集団からランダムに抽出されている。
- 完全な多重共線性がない: 説明変数間に完全な相関関係がない。
- ゼロ条件付き期待値: 誤差項の期待値は、任意の説明変数の値が与えられた下でゼロである (E[u | X] = 0)。これは「説明変数が外生的である」とも言われ、不偏性のための最も重要な仮定です。
このリストに「誤差項の正規分布」や「誤差項の系列相関がないこと」は含まれていないことに注目してください。
1. 誤差項が正規分布に従っていない場合
結論:不偏性は保たれます。
- 理由: 上記の不偏性のための条件(特に E[u|X] = 0)に、誤差項の分布が正規分布であるという仮定は含まれていません。したがって、誤差項がどのような分布に従っていようとも、E[u|X] = 0 が満たされていれば、最小二乗推定量は不偏性を持ちます。
- 影響: 正規分布の仮定は、不偏性ではなく、主に検定(t検定やF検定)の信頼性に関わってきます。
- 小標本の場合: 誤差項が正規分布でないと、t分布やF分布が使えず、検定が正確でなくなります。
- 大標本の場合: 中心極限定理により、標本サイズが十分に大きければ、誤差項が正規分布でなくても最小二乗推定量は近似的に正規分布に従います。そのため、大標本では検定や信頼区間の推定が頑健(ロバスト)に行えます。
2. 誤差項に系列相関(自己相関)がある場合
結論:不偏性が満たされない可能性が高いです。
系列相関とは、ある時点の誤差項 u_t が、他の時点の誤差項 u_{t-1}, u_{t-2}, ... と相関を持つ状況です。これはガウス=マルコフの仮定の1つである「誤差項の無相関」に違反します。
この違反が不偏性にどう影響するかは、モデルの形によります。
ケースA:説明変数が「厳密に外生的」な場合
- 状況: モデルの説明変数Xが、過去・現在・未来すべての誤差項uと無相関である場合。これは経済学の静学モデルなどでは仮定されることがありますが、時系列データでは稀です。
- 結論: この(非常に強い)仮定が満たされるなら、系列相関があっても不偏性は保たれます。
- ただし: 推定量の分散が最小ではなくなるため、OLSは最良線形不偏推定量(BLUE)ではなくなります。つまり、より効率的(分散が小さい)な推定量(例えば、一般化最小二乗法 GLS)が存在します。また、標準誤差の計算が不正確になり、t検定などが信頼できなくなります。
ケースB:説明変数に「被説明変数のラグ」が含まれる場合(動学モデル)
- 状況:
y_t = β_0 + β_1 * y_{t-1} + u_tのようなモデルを考えます。ここで説明変数としてy_{t-1}が含まれています。 - 結論: この場合、誤差項に系列相関があると、最小二乗推定量は不偏性を失い、バイアス(偏り)が生じます。また、一致性(標本サイズを無限大にすると推定量が真の値に収束する性質)も失います。
- 理由(直感的説明):
-
y_{t-1}は、1期前の誤差項u_{t-1}の影響を受けています。 - 誤差項に系列相関があるため、
u_tはu_{t-1}と相関しています。 - したがって、
u_tはy_{t-1}と相関してしまいます。 - これは、不偏性のための最も重要な仮定である「誤差項と説明変数が無相関(E[u|X]=0)」に違反します。結果として、推定量にバイアスが生じます。
-
3. まとめ
| 条件 | 不偏性 (Unbiasedness) | 一致性 (Consistency) | 効率性 (BLUE) | 検定・信頼区間 |
|---|---|---|---|---|
| 誤差項が正規分布でない | 〇 (保たれる) | 〇 (保たれる) | 〇 (保たれる) | 小標本では×、大標本では〇 (CLT) |
| 系列相関がある (説明変数が厳密に外生的) | 〇 (保たれる) | 〇 (保たれる) | × (失われる) | × (標準誤差が不正確) |
| 系列相関がある (説明変数にラグ変数を含む) | × (失われる) | × (失われる) | × (失われる) | × (すべて信頼できない) |
要約すると、不偏性のための生命線は「誤差項と説明変数の無相関(E[u|X]=0)」です。 正規分布の仮定はこれに影響しませんが、系列相関の存在は、特に動学モデルにおいてこの生命線を断ち切ってしまうため、深刻な問題を引き起こすのです。
2. Rによるシミュレーション
1. 準備
まず、必要なライブラリを読み込みます。
# --- 0. 準備: 必要なライブラリの読み込み ---
library(ggplot2)
library(dplyr)
library(tidyr)
result_output <- "D:/result_output"2. シミュレーションのコード
以下に、データ生成からシミュレーションの実行、結果の確認までのコードを示します。
# --- 1. シミュレーションの基本設定 ---
seed <- 20250704
n_sim <- 2000 # 各シナリオ・サンプルサイズでのシミュレーション回数
true_beta0 <- 2.0 # 真の切片 (α)
true_beta1 <- 0.5 # 真の傾き (β)
# テストするサンプルサイズ
sample_sizes <- c(50, 200, 1000, 4000)
# 系列相関のパラメータ
rho <- 0.8 # AR(1)モデルの自己相関係数 u_t = rho * u_{t-1} + e_t
# 結果を格納するための空のリスト
results_list <- list()# --- 2. シミュレーションの実行 ---
set.seed(seed)
# サンプルサイズごとにループ
for (n in sample_sizes) {
# シミュレーション回数だけループ
for (i in 1:n_sim) {
# --- パターン1: 誤差項が正規分布でない ---
x1 <- rnorm(n, mean = 10, sd = 3)
u1 <- rt(n, df = 3)
y1 <- true_beta0 + true_beta1 * x1 + u1
fit1 <- lm(y1 ~ x1)
# --- パターン2: 系列相関あり & 説明変数が厳密に外生的 ---
x2 <- rnorm(n, mean = 10, sd = 3)
u2 <- arima.sim(model = list(ar = rho), n = n, sd = 1)
y2 <- true_beta0 + true_beta1 * x2 + u2
fit2 <- lm(y2 ~ x2)
# --- パターン3: 系列相関あり & 説明変数にラグ変数を含む ---
u3 <- numeric(n + 1)
y3 <- numeric(n + 1)
e3 <- rnorm(n + 1, sd = 1)
y3[1] <- true_beta0 / (1 - true_beta1)
u3[1] <- e3[1] / sqrt(1 - rho^2)
for (t in 2:(n + 1)) {
u3[t] <- rho * u3[t - 1] + e3[t]
y3[t] <- true_beta0 + true_beta1 * y3[t - 1] + u3[t]
}
y_t <- y3[2:(n + 1)]
y_lag <- y3[1:n]
fit3 <- lm(y_t ~ y_lag)
# 結果をリストに追加
results_list[[length(results_list) + 1]] <- data.frame(
sample_size = n,
simulation_id = i,
scenario = c(
"1. 誤差項が非正規分布",
"2. 系列相関あり (説明変数が外生的)",
"3. 系列相関あり (ラグ変数を含む)"
),
estimated_beta1 = c(coef(fit1)[2], coef(fit2)[2], coef(fit3)[2])
)
}
# 進捗表示
# cat("サンプルサイズ n =", n, "のシミュレーションが完了しました。\n")
}
# リストを一つのデータフレームに変換
results_df <- bind_rows(results_list)
# シミュレーション結果の保存
setwd(result_output)
saveRDS(object = results_df, file = "ols_unbiasedness_consistency.rds")# tbl オブジェクトの読み込み
setwd(result_output)
results_df <- readRDS("ols_unbiasedness_consistency.rds")
# --- 3. 結果の確認(不偏性と一致性) ---
# 3-1. 不偏性の確認 (推定量の平均値)
unbiased_check <- results_df %>%
group_by(scenario, sample_size) %>%
summarise(mean_beta1_hat = mean(estimated_beta1), .groups = "drop") %>%
mutate(bias = mean_beta1_hat - true_beta1)
cat("--- 不偏性の確認 (真のβ1 = ", true_beta1, ") ---\n")
unbiased_check %>% knitr::kable()--- 不偏性の確認 (真のβ1 = 0.5 ) ---| scenario | sample_size | mean_beta1_hat | bias |
|---|---|---|---|
| 1. 誤差項が非正規分布 | 50 | 0.4994779 | -0.0005221 |
| 1. 誤差項が非正規分布 | 200 | 0.4981397 | -0.0018603 |
| 1. 誤差項が非正規分布 | 1000 | 0.4993246 | -0.0006754 |
| 1. 誤差項が非正規分布 | 4000 | 0.5001447 | 0.0001447 |
| 2. 系列相関あり (説明変数が外生的) | 50 | 0.5000689 | 0.0000689 |
| 2. 系列相関あり (説明変数が外生的) | 200 | 0.4997442 | -0.0002558 |
| 2. 系列相関あり (説明変数が外生的) | 1000 | 0.5003112 | 0.0003112 |
| 2. 系列相関あり (説明変数が外生的) | 4000 | 0.5000392 | 0.0000392 |
| 3. 系列相関あり (ラグ変数を含む) | 50 | 0.8959624 | 0.3959624 |
| 3. 系列相関あり (ラグ変数を含む) | 200 | 0.9213662 | 0.4213662 |
| 3. 系列相関あり (ラグ変数を含む) | 1000 | 0.9273889 | 0.4273889 |
| 3. 系列相関あり (ラグ変数を含む) | 4000 | 0.9282349 | 0.4282349 |
- パターン1 (誤差項が非正規分布) と パターン2 (系列相関あり (説明変数が外生的)):
- どのサンプルサイズでも、
mean_beta1_hat(推定量の平均値) は、真の値0.5に近く、bias` (バイアス) は、ほぼゼロです。 - これは、これらのシナリオで最小二乗推定量が不偏性を持つことを示唆しています。
- どのサンプルサイズでも、
- パターン3 (系列相関あり (ラグ変数を含む)):
- どのサンプルサイズでも、
mean_beta1_hatは、真の値0.5から外れており(約0.90~0.93)、biasは明らかに正の値を取っており、ゼロではありません。 - これは、このシナリオで最小二乗推定量が不偏性を持たない(バイアスがある)ことを示唆しています。
- どのサンプルサイズでも、
# 3-2. 一致性の確認 (4行3列のグリッドプロット)
# --- パネルの順序を指定するための準備 ---
# 1. シナリオの順序を定義 (データフレーム内の日本語と一致させる)
scenario_levels <- c(
"1. 誤差項が非正規分布",
"2. 系列相関あり (説明変数が外生的)",
"3. 系列相関あり (ラグ変数を含む)"
)
# 2. サンプルサイズの順序を定義
sample_size_levels <- c("n = 50", "n = 200", "n = 1000", "n = 4000")
# 3. プロット用のデータフレームを作成し、ファクターを適用
results_df_plot <- results_df %>%
mutate(
scenario = factor(scenario, levels = scenario_levels),
sample_size_factor = factor(paste("n =", sample_size), levels = sample_size_levels)
)
# 4. geom_vlineで使う平均値データも、同じファクターで作成
unbiased_check_plot <- results_df_plot %>%
group_by(scenario, sample_size_factor) %>%
summarise(mean_beta1_hat = mean(estimated_beta1), .groups = "drop")
# --- プロットの作成 (facet_gridを使用) ---
consistency_grid_plot <- ggplot(results_df_plot, aes(x = estimated_beta1)) +
geom_density(aes(fill = scenario), alpha = 0.7, show.legend = FALSE) +
geom_vline(xintercept = true_beta1, color = "red", linetype = "dashed", size = 1) +
geom_vline(
data = unbiased_check_plot, aes(xintercept = mean_beta1_hat, color = scenario),
linetype = "solid", size = 0.8, show.legend = FALSE
) +
facet_grid(sample_size_factor ~ scenario, scales = "free_y") +
scale_fill_brewer(palette = "Set1") +
scale_color_brewer(palette = "Set1") +
labs(
title = "最小二乗推定量の分布と一致性の確認(シナリオ・サンプルサイズ別)",
subtitle = paste("赤い破線: 真のβ1 =", true_beta1, " | 各パネル内の実線: 推定量の平均値"),
x = "β1の推定量 (b1)",
y = "密度"
) +
theme_minimal() +
theme(
legend.position = "none",
axis.text.x = element_text(angle = 45, hjust = 1),
strip.text = element_text(size = 9)
)
cat("--- 一致性確認グリッドプロット ---\n")
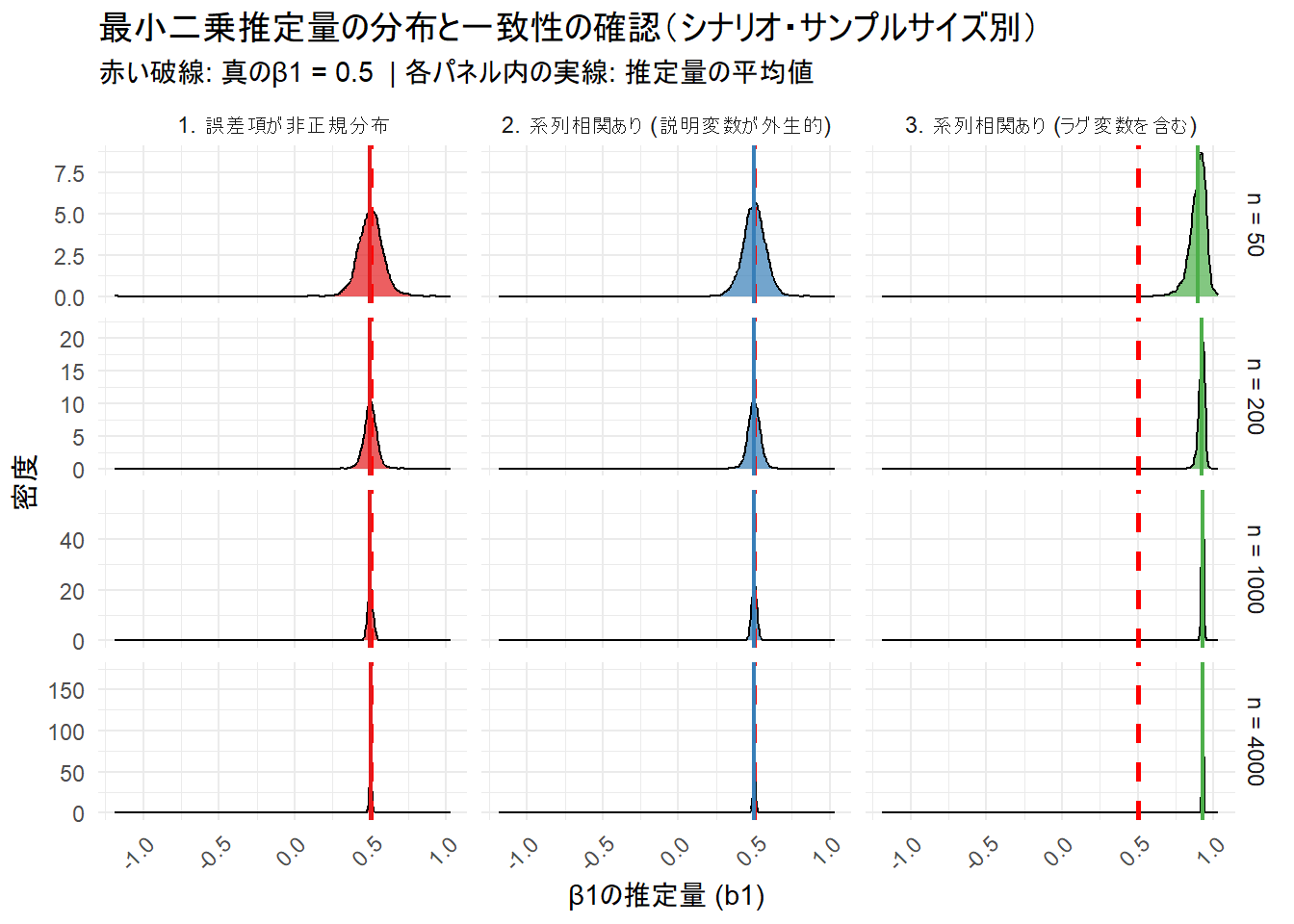
print(consistency_grid_plot)--- 一致性確認グリッドプロット ---- 赤い破線は真の値 (
0.5) を示します。 - 各色の実線は、各シナリオにおける推定量の平均値を示します。
- 分布の山が、サンプルサイズ(
n)が大きくなるにつれてどのように変化するかに注目してください。 - パターン1 (誤差項が非正規分布) と パターン2 (系列相関あり (説明変数が外生的)):
-
nが小さい時 (n=50)、分布は幅広く広がっています。 -
nが大きく (n=4000) なるにつれて、分布は真の値(赤い破線)の周りにどんどん狭く、鋭くなっていきます。 - これは、サンプルサイズを増やせば推定値が真の値に収束していく一致性を持つことを示しています。
- また、分布の中心(平均値)は常に真の値と一致しており(プロットでは重なり見えなくなっています)、不偏性も見て取れます。
-
- パターン3 (系列相関あり (ラグ変数を含む)):
-
nが小さい時、分布は幅広いです。 -
nが大きくなるにつれて、分布は確かに狭く、鋭くなっていきます。 - しかし、その収束先は真の値(赤い破線)ではありません。 分布は、バイアスを含んだ値(
0.928付近)に収束していきます。 - これは、この推定量が一致性を持たないことを意味します。サンプルサイズをいくら増やしても、誤った値に収束してしまうのです。
-
3. まとめ
このシミュレーションから、理論通りの以下の結論が直感的に確認できました。
| パターン | 不偏性 (Unbiasedness) | 一致性 (Consistency) |
|---|---|---|
| 1. 誤差項が正規分布でない | 〇 | 〇 |
| 2. 系列相関あり(説明変数が外生的) | 〇 | 〇 |
| 3. 系列相関あり(説明変数にラグ変数) | ✕ | ✕ |
このように、最小二乗推定量の性質を議論する際には、「誤差項に系列相関があるか」だけでなく、「説明変数がどのような性質を持つか(特にラグ付きの被説明変数を含んでいるか)」が決定的に重要であることがわかります。
以上です。