Rで構造VARモデルと誘導VARモデル

Rで 構造VARモデルと誘導VARモデル を確認します。

1. 構造VARモデルと誘導VARモデルの解説

VAR（Vector Autoregression）モデルは、複数の時系列変数間の動的な関係を分析するためのモデルです。VARモデルには大きく分けて「誘導VARモデル」と「構造VARモデル」の2種類があり、分析の目的によって使い分けられます。

1.1. 誘導VARモデル (Reduced Form VAR Model)

一般的に「VARモデル」という場合、この誘導VARモデルを指します。このモデルは、各変数の現在値を、すべての変数の過去の値の線形和と誤差項で表現します。

2変数（\(y_{1,t}\), \(y_{2,t}\)）でラグが1のVAR(1)モデルを例にとると、以下のように表せます。

\[\begin{eqnarray}
y_{1,t} &=& c_1 + a_{11,1} y_{1,t-1} + a_{12,1} y_{2,t-1} + u_{1,t}\\
y_{2,t} &=& c_2 + a_{21,1} y_{1,t-1} + a_{22,1} y_{2,t-1} + u_{2,t}
\end{eqnarray}\]

ここで、

\(y_{1,t}\), \(y_{2,t}\)：時刻\(t\)における各変数
\(c_1, c_2\)：定数項
\(a_{ij,1}\)：ラグ1の係数パラメータ
\(u_{1,t}, u_{2,t}\)：誘導型の誤差項（Reduced form errors）

このモデルの特徴は、誤差項 \(u_{1,t}\) と \(u_{2,t}\) が互いに相関を持つことを許容する点です（\(Cov(u_{1,t}, u_{2,t}) \neq 0\)）。これは、モデルで説明しきれない、同時（同じ時点\(t\)で起こる）の相関関係が誤差項に含まれていることを意味します。

誘導VARモデルは、各方程式を単純な最小二乗法（OLS）で推定でき、予測やグレンジャー因果性の検定などに利用されます。しかし、誤差項間の相関のため、ある変数に変化（ショック）が起きたとき、その影響がどの変数に由来するものなのかを特定することが困難です。

1.2. 構造VARモデル (Structural VAR, SVAR Model)

構造VARモデルは、誘導VARモデルに例えば 経済理論に基づいた変数間の同時的な因果関係 のような構造を導入したモデルです。これにより、ショックの源泉を特定し、その影響を分析すること（インパルス応答関数分析）が可能になります。

SVAR(1)モデルの例は以下の通りです。

\[\begin{eqnarray}
y_{1,t} + b_{12} y_{2,t} &=& \Gamma_{11,1} y_{1,t-1} + \Gamma_{12,1} y_{2,t-1} + \epsilon_{1,t}\\
y_{2,t} + b_{21} y_{1,t} &=& \Gamma_{21,1} y_{1,t-1} + \Gamma_{22,1} y_{2,t-1} + \epsilon_{2,t}
\end{eqnarray}\]

ここで、

\(b_{12}, b_{21}\)：変数間の同時的な関係を表す係数。例えば、\(b_{21} \neq 0\) は「\(y_1\)が\(y_2\)に同時に影響を与える」ことを示す。
\(\epsilon_{1,t}, \epsilon_{2,t}\)：構造ショック（Structural shocks）
\(\Gamma\): ラグ変数の係数行列

このモデルの特徴は、構造ショック \(\epsilon_{1,t}\) と \(\epsilon_{2,t}\) が互いに無相関であると仮定される点です（\(Cov(\epsilon_{1,t}, \epsilon_{2,t}) = 0\)）。これらは、例えば経済学的の場合では解釈可能な、根源的なショック（例：金融政策ショック、技術ショックなど）と見なされます。

1.3. 両者の関係と識別問題

SVARモデルの式を、左辺に現在の変数 \(y_t\) を集めるように行列で書き直すと、

\[
\begin{pmatrix}
1 & b_{12} \\
b_{21} & 1
\end{pmatrix}
\begin{pmatrix}
y_{1,t} \\
y_{2,t}
\end{pmatrix}
= \Gamma_1 y_{t-1} +
\begin{pmatrix}
\epsilon_{1,t} \\
\epsilon_{2,t}
\end{pmatrix}
\]

この左辺の係数行列を A と書くと、 \(A y_t = \Gamma_1 y_{t-1} + \epsilon_t\) となります。この両辺に左から \(A^{-1}\) を掛けると、

\(y_t = A^{-1} \Gamma_1 y_{t-1} + A^{-1}\epsilon_t\)

となり、これは誘導VARモデルの形をしています（\(a = A^{-1} \Gamma_1\), \(u_t = A^{-1}\epsilon_t\)）。誘導VARの誤差項 \(u_t\) は、構造ショック \(\epsilon_t\) を用いて \(u_t = A^{-1}\epsilon_t\) と表せることがわかります。

問題は、私たちがデータから直接推定できるのは誘導VARモデルのパラメータ（係数\(a\)と誤差項の分散共分散行列 \(\Sigma_u\)）だけであるという点です。そこからSVARモデルのパラメータ（\(A\)など）を一意に特定することはできません。これを識別問題と呼びます。

この問題を解決するため、経済理論などに基づいて\(A\)行列に何らかの制約（例えば、一部の要素を0と仮定する）を課す必要があります。最も一般的な制約が再帰的制約（Recursive restriction）で、これは「ある変数は他の変数に同時に影響を与えるが、その逆はない」という階層構造を仮定するもので、数学的にはコレスキー分解に対応します。

2. Rによるシミュレーション

それでは、この関係をシミュレーションで確認してみましょう。

シミュレーションの流れ

真のSVARモデルを設定: こちらで真の経済構造（SVARモデルのパラメータ）を決めます。
データ生成: そのSVARモデルから時系列データを生成します。
誘導VARモデルの推定: 生成したデータを使って、誘導VARモデルを推定します。
構造VARモデルの推定: 適切な識別制約（今回は再帰的制約）を課してSVARモデルを推定し、元の構造を復元できるか確認します。

2.1. Rコード

# パッケージのロード
library(vars)
library(ggplot2)
library(tidyr)
library(dplyr)
library(patchwork)

seed <- 20250704
set.seed(seed)

# --- Step 1 & 2: 真のSVARモデルの設定とデータ生成 ---

# シミュレーションのパラメータ
n_obs <- 500 # データ点数
burn_in <- 100 # 初期値の影響を捨てる期間

# 真のSVARモデルを定義します。
# y1_t                = 0.7*y1_{t-1} + 0.2*y2_{t-1} + e1_t
# y2_t + b21*y1_t     = 0.1*y1_{t-1} + 0.6*y2_{t-1} + e2_t
#
# 今回は、y1がy2に同時的な影響を与えると仮定します。
# b21 = -0.5 と設定します。つまり、y2_t - 0.5*y1_t = ... という構造です。
#
# この構造を  (A * y_t = Gamma * y_{t-1} + epsilon_t) の行列 で表現します。
#
# | 1    b12 | | y1_t |   | G11  G12 | | y1_{t-1} |   | e1_t |
# |          | |      | = |          | |          | + |      |
# | b21  1   | | y2_t |   | G21  G22 | | y2_{t-1} |   | e2_t |
#
# 制約: b12 = 0 (y2はy1に同時影響を与えない)
# 真の値: b21 = -0.5 (y1はy2に同時影響を与える)

Amat_true <- matrix(c(1, -0.5, 0, 1), nrow = 2, byrow = FALSE)
Gamma1_true <- matrix(c(0.7, 0.2, 0.1, 0.6), nrow = 2, byrow = TRUE)

cat("--- 真のSVARモデルのパラメータ ---\n")
cat("A (同時係数行列):\n")
print(Amat_true)
cat("\nGamma1 (ラグ係数行列):\n")
print(Gamma1_true)

# 誘導VARのパラメータに変換
Amat_true_inv <- solve(Amat_true)
A1_true <- Amat_true_inv %*% Gamma1_true

# データ生成
# 構造ショックを生成 (平均0, 分散1, 無相関)
e <- matrix(rnorm(2 * (n_obs + burn_in)), ncol = 2)
# 誘導VARの誤差項を生成 u = A^-1 * e
u <- t(Amat_true_inv %*% t(e))

# 時系列データを格納する行列
y <- matrix(0, nrow = n_obs + burn_in, ncol = 2)
colnames(y) <- c("y1", "y2")

# VAR(1)プロセスでデータを生成
for (t in 2:(n_obs + burn_in)) {
  y[t, ] <- A1_true %*% y[t - 1, ] + u[t, ]
}

# 初期値の影響を捨てる
y_final <- as.data.frame(y[(burn_in + 1):(n_obs + burn_in), ])
y_final$time <- 1:n_obs

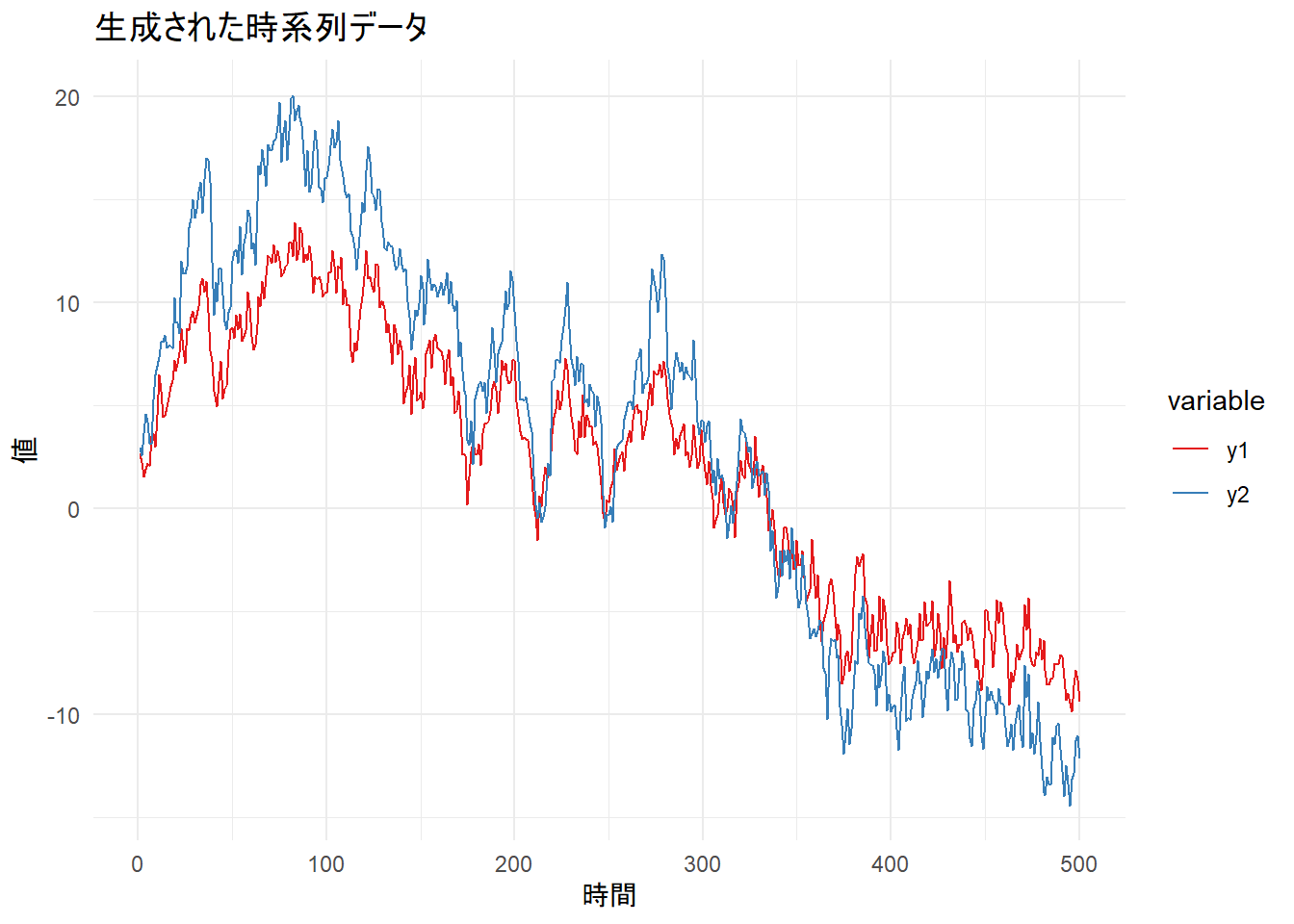
# 生成したデータのプロット
p_data <- y_final %>%
  pivot_longer(cols = c(y1, y2), names_to = "variable", values_to = "value") %>%
  ggplot(aes(x = time, y = value, color = variable)) +
  geom_line() +
  labs(title = "生成された時系列データ", x = "時間", y = "値") +
  theme_minimal() +
  scale_color_brewer(palette = "Set1")
print(p_data)

--- 真のSVARモデルのパラメータ ---
A (同時係数行列):
     [,1] [,2]
[1,]  1.0    0
[2,] -0.5    1

Gamma1 (ラグ係数行列):
     [,1] [,2]
[1,]  0.7  0.2
[2,]  0.1  0.6

# --- Step 3: 誘導VARモデルの推定 ---
var_est <- VAR(y_final[, c("y1", "y2")], p = 1, type = "none")

cat("\n--- 誘導VARモデルの推定結果の確認 ---\n\n")

# 1. ラグ係数行列の比較
cat("【1. ラグ係数行列 A1 の比較】\n")
cat("真のA1行列:\n")
print(A1_true)

cat("\n推定されたA1行列:\n")
# var_estオブジェクトから係数を抽出
A1_est <- coef(var_est)$y1[, 1:2] # y1の式から抽出
print(Acoef(var_est)[[1]])

# 2. 誤差項の分散共分散行列の比較
cat("\n\n【2. 誤差項の分散共分散行列 Σ_u の比較】\n")
# 真の誤差項の分散共分散行列を計算
Sigma_u_true <- Amat_true_inv %*% t(Amat_true_inv) # 構造ショックの分散が1の場合
cat("真のΣ_u行列:\n")
print(Sigma_u_true)

cat("\n推定されたΣ_u行列:\n")
# var_estのsummaryから抽出
print(summary(var_est)$covres)

# --- Step 4: 構造VARモデルの推定 ---
# データ生成時に課した「y2からy1への同時効果はない」という制約を Amat で指定します。
# 0: 0に制約するパラメータ
# 1: 正規化のために1に固定するパラメータ
A_constraint <- matrix(NA, nrow = 2, ncol = 2)
diag(A_constraint) <- 1 # 対角要素は1に正規化
A_constraint[1, 2] <- 0 # y2からy1への同時効果を0に制約 (b12=0)
# A_constraint[2, 1]はNAのまま(y1からy2への効果を推定)

# SVARモデルを推定
svar_est <- SVAR(var_est, Amat = A_constraint)

cat("\n--- 推定されたSVARモデルの行列 (同時係数行列) ---\n")
print(svar_est)


--- 誘導VARモデルの推定結果の確認 ---

【1. ラグ係数行列 A1 の比較】
真のA1行列:
     [,1] [,2]
[1,] 0.70  0.2
[2,] 0.45  0.7

推定されたA1行列:
       y1.l1     y2.l1
y1 0.7138321 0.1869578
y2 0.4108390 0.7226496


【2. 誤差項の分散共分散行列 Σ_u の比較】
真のΣ_u行列:
     [,1] [,2]
[1,]  1.0 0.50
[2,]  0.5 1.25

推定されたΣ_u行列:
          y1      y2
y1 0.9703132 0.50769
y2 0.5076900 1.28418

--- 推定されたSVARモデルの行列 (同時係数行列) ---

SVAR Estimation Results:
======================== 


Estimated A matrix:
        y1 y2
y1  1.0000  0
y2 -0.5216  1