Rで標準ブラウン運動

Rで 標準ブラウン運動 を確認します。

1. 標準ブラウン運動とは？

標準ブラウン運動（Standard Brownian Motion）は、確率過程の一種で、時間とともにランダムに変動する現象をモデル化するために用いられます。しばしば記号 \(B(t)\) や \(W(t)\) で表されます。

物理的には、液体中の微粒子（花粉など）が、水分子の不規則な衝突によってランダムに動く「ブラウン運動」を数学的に記述したものです。金融工学では、株価や為替レートのランダムな変動の基礎モデルとして利用されています。

標準ブラウン運動は、以下の3つの性質によって定義されます。

出発点は0: \(B(0) = 0\)
- 時刻0では、必ず原点（値が0）からスタートします。
独立な増分 (Independent Increments):
- 重ならない時間区間での動き（増分）は、互いに独立です。例えば、時刻0から1までの動きと、時刻1から2までの動きには何の関連もありません。これは「過去の動きが未来の動きを予測する情報を持たない」というマルコフ性を意味します。
正規分布に従う増分 (Normal Increments):
- 任意の時刻 \(s\) と \(t\) (\(s < t\)) における増分 \(B(t) - B(s)\) は、平均が0で、分散が時間差 \(t-s\) となる正規分布 \(N(0, t-s)\) に従います。
- つまり、時間が長く経過するほど、変動の幅（分散）が大きくなることを意味します。

これらの性質から、標準ブラウン運動の軌跡（サンプルパス）は、連続であるにもかかわらず、どの点においても微分不可能（ギザギザしている）になります。

2. Rによるシミュレーション

このブラウン運動をシミュレーションするには、時間を細かいステップに区切って、各ステップでの微小なランダムな動きを足し合わせていきます。

シミュレーションの考え方

時刻を \(0, \Delta t, 2\Delta t, \dots, T\) と細かく区切ります。性質3より、微小時間 \(\Delta t\) の間の動き \(B(t_{i}) - B(t_{i-1})\) は、平均0、分散 \(\Delta t\) の正規分布に従います。

これは、標準正規分布（平均0、分散1）に従う乱数 \(Z_i\) を用いて、\(\sqrt{\Delta t} \times Z_i\) と表現できます。

したがって、各時刻のブラウン運動の値 \(B(t_i)\) は、以下のように計算できます。

\(B(t_0) = B(0) = 0\)
\(B(t_i) = B(t_{i-1}) + \sqrt{\Delta t} \times Z_i\)

これは、微小なランダムな動きの累積和を計算することに他なりません。

Rコードと実行例

以下に、R言語を利用して、複数の標準ブラウン運動のサンプルパスを生成し、プロットするコードを示します。

シミュレーションコード:

# 必要なライブラリを読み込む
library(ggplot2)
library(dplyr)
library(tidyr)

# シミュレーションのパラメータを設定
T <- 1 # 最終時刻 (例: 1年)
n <- 1000 # 時間ステップの数
dt <- T / n # 時間ステップの幅
n_paths <- 5 # シミュレーションするパス（軌跡）の数

# 再現性のために乱数シードを固定
seed <- 20250703
set.seed(seed)

# 1. 標準正規分布に従う乱数を (n x n_paths) の行列として生成
Z <- matrix(rnorm(n * n_paths, mean = 0, sd = 1), nrow = n, ncol = n_paths)

# 2. ブラウン運動の増分を計算
dB <- sqrt(dt) * Z

# 3. 増分の累積和を計算して、ブラウン運動のパスを作成
# apply関数を使い、各列（パスごと）に累積和 (cumsum) を適用
B <- apply(dB, 2, cumsum)

# 4. 各パスの初期値 B(0)=0 を行列の先頭に追加
B <- rbind(rep(0, n_paths), B)

# 5. 時間軸のデータを作成
time <- seq(0, T, by = dt)

# 6. ggplotで扱いやすいようにデータを整形
# まずはデータフレームに変換
df <- as.data.frame(B)
# 列名を分かりやすくする
colnames(df) <- paste0("Path_", 1:n_paths)
# 時間列を追加
df$time <- time

# tidyr::pivot_longer を使って「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -time, # time列以外を対象
    names_to = "path", # 新しい列名（パスIDが入る）
    values_to = "value" # 新しい列名（B(t)の値が入る）
  )

# 7. ggplot2でプロット
p <- ggplot(df_long, aes(x = time, y = value, color = path, group = path)) +
  geom_line(alpha = 0.8) +
  geom_hline(yintercept = 0, linetype = "dashed", color = "black") + # B(0)=0 の基準線
  labs(
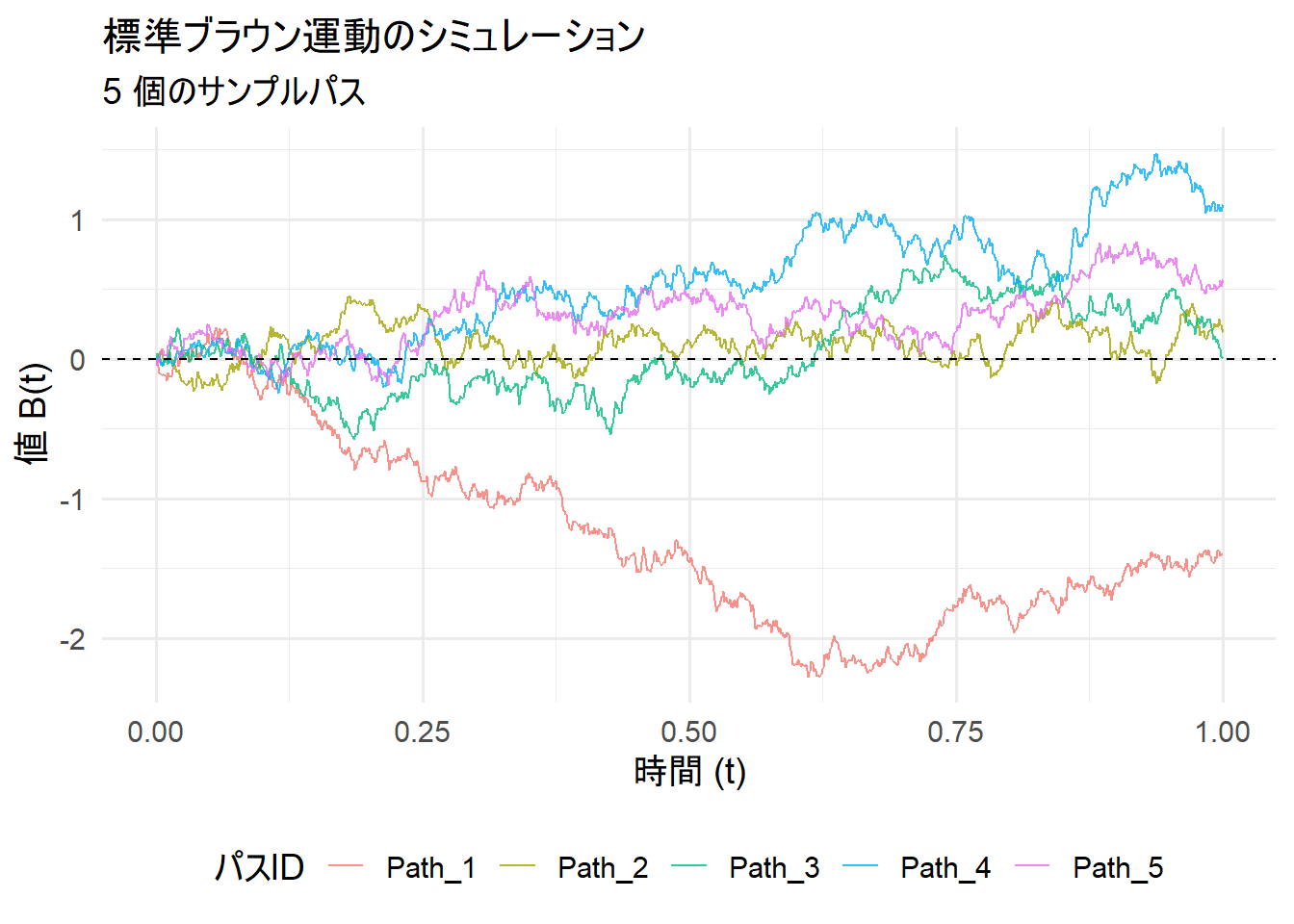
    title = "標準ブラウン運動のシミュレーション",
    subtitle = paste(n_paths, "個のサンプルパス"),
    x = "時間 (t)",
    y = "値 B(t)",
    color = "パスID"
  ) +
  theme_minimal(base_size = 14) +
  theme(legend.position = "bottom")

# プロットを表示
print(p)