Rで 正規分布の再生性 を確認します。
「正規分布の再生性」とは?
正規分布の再生性(Reproductive property of the normal distribution)とは、「互いに独立な複数の正規分布に従う確率変数の和もまた、正規分布に従う」という性質のことです。
具体的に数式で説明します。
2つの独立な確率変数 \(X\) と \(Y\) が、それぞれ以下の正規分布に従うとします。
- \(X \sim N(\mu_1, \sigma_1^2)\) (平均 \(\mu_1\), 分散 \(\sigma_1^2\) の正規分布)
- \(Y \sim N(\mu_2, \sigma_2^2)\) (平均 \(\mu_2\), 分散 \(\sigma_2^2\) の正規分布)
このとき、これらの和から作られる新しい確率変数 \(Z = X + Y\) は、以下の正規分布に従います。
- \(Z \sim N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)\)
つまり、和の分布の平均は元の平均の和になり、分散も元の分散の和になります。このシンプルで性質が「再生性」と呼ばれます。
この性質は、統計学の多くの場面で非常に重要です。例えば、標本平均の分布を考える際などに中心的な役割を果たします。
Rによるシミュレーション
それでは、この「正規分布の再生性」をシミュレーションで確認してみましょう。
- 独立な2つの正規分布から多数のサンプルを生成します。
- それらのサンプルを足し合わせます。
- 足し合わせた結果の分布が、理論上の正規分布と一致するかをヒストグラムと確率密度曲線で比較します。
1. 準備
まず、シミュレーションとプロット作成に必要なライブラリを読み込みます。
# データ操作とプロット作成のためのライブラリを読み込み
library(dplyr)
library(ggplot2)
seed <- 202507062. サンプルデータの作成
2つの異なる正規分布から、それぞれ10,000個のサンプル(乱数)を生成します。
- X: 平均 10, 標準偏差 2 の正規分布 \(N(10, 2^2)\)
- Y: 平均 20, 標準偏差 3 の正規分布 \(N(20, 3^2)\)
set.seed(seed)
# シミュレーションのパラメータを設定
n_samples <- 10000 # サンプルサイズ
# Xのパラメータ
mu1 <- 10
sd1 <- 2
# Yのパラメータ
mu2 <- 20
sd2 <- 3
# 正規分布に従う乱数を生成
x <- rnorm(n = n_samples, mean = mu1, sd = sd1)
y <- rnorm(n = n_samples, mean = mu2, sd = sd2)
# 2つの確率変数の和を計算
z <- x + y3. 理論値の計算
正規分布の再生性に基づき、和 \(Z = X + Y\) が従う正規分布の理論的なパラメータを計算します。
- 理論上の平均: \(\mu_z = \mu_1 + \mu_2 = 10 + 20 = 30\)
- 理論上の分散: \(\sigma_z^2 = \sigma_1^2 + \sigma_2^2 = 2^2 + 3^2 = 4 + 9 = 13\)
- 理論上の標準偏差: \(\sigma_z = \sqrt{13} \approx 3.60555\)
# Zの理論的なパラメータ
mu_z_theory <- mu1 + mu2
sd_z_theory <- sqrt(sd1^2 + sd2^2)4. シミュレーション結果の可視化
生成されたサンプル z の分布(ヒストグラム)と、理論上の正規分布の確率密度関数を重ねてプロットし、両者がどれほど一致するかを視覚的に確認します。
# データをプロットしやすいようにデータフレームに格納
df <- data.frame(Z = z)
# ggplotで可視化
ggplot(df, aes(x = Z)) +
# ヒストグラムを描画 (y軸を確率密度に変換)
geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "skyblue", color = "white", alpha = 0.8) +
# 理論上の正規分布の確率密度関数を重ねて描画
stat_function(
fun = dnorm, # 正規分布の確率密度関数を指定
args = list(mean = mu_z_theory, sd = sd_z_theory), # 理論値を引数として渡す
color = "red",
linewidth = 1.2
) +
# ラベルとタイトルを設定
labs(
title = "正規分布の再生性のシミュレーション",
subtitle = paste0(
"サンプル(Z = X + Y)の分布と理論上の正規分布 N(",
round(mu_z_theory, 2), ", ", round(sd_z_theory^2, 2), ")"
),
x = "Z = X + Y の値",
y = "確率密度"
) +
theme_minimal()プロットの解説
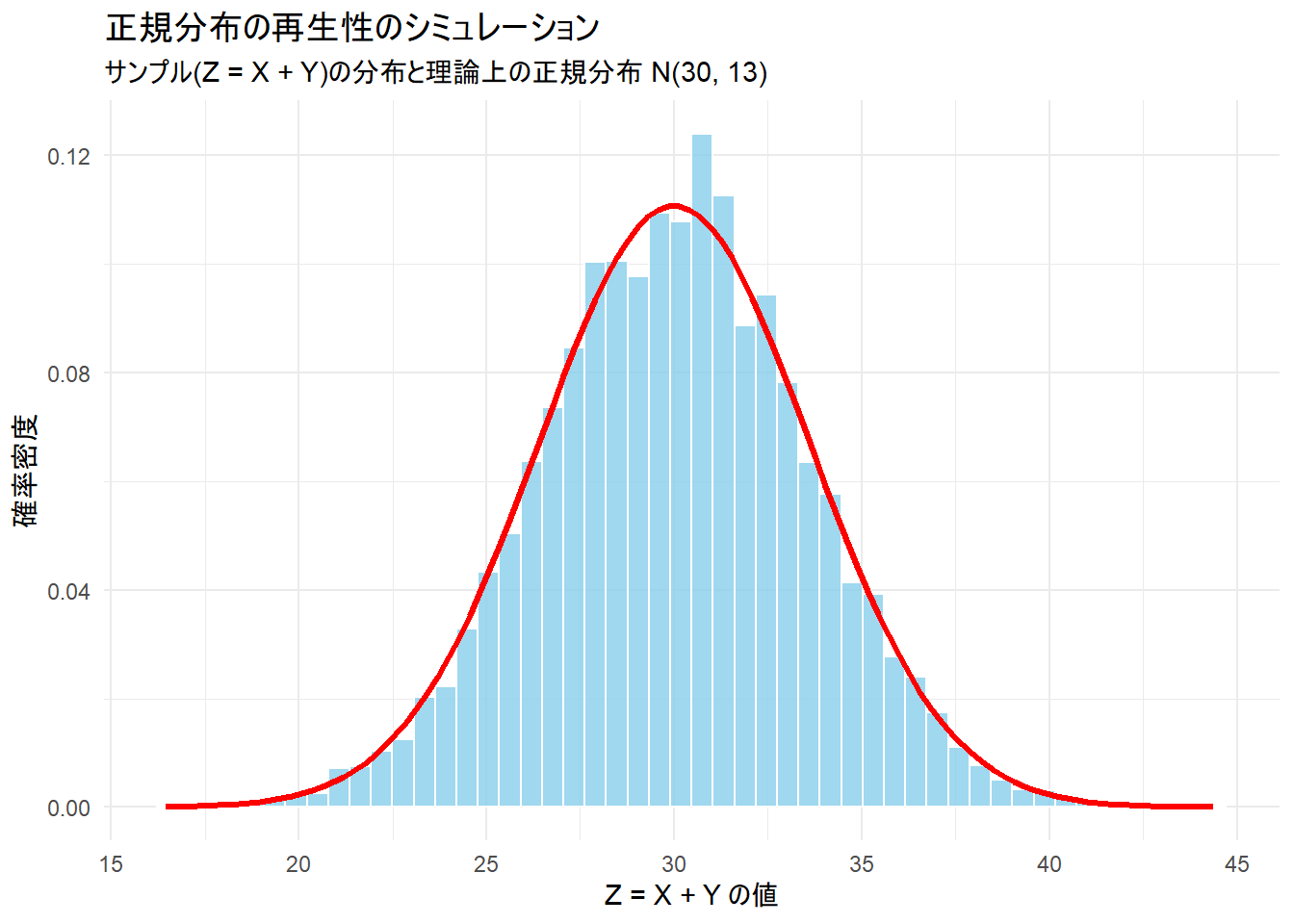
上記のコードを実行すると、以下のプロットが生成されます。
- 水色のヒストグラム: 実際に2つの正規分布からのサンプルを足し合わせて得られたデータ
zの分布です。 - 赤い曲線: 再生性の理論から導かれた「平均 30, 標準偏差 \(\sqrt{13}\)」の正規分布の確率密度関数です。
ご覧の通り、シミュレーションによって得られたヒストグラムの形状は、理論上の正規分布曲線とほぼ一致しています。
5. 数値による確認
最後に、シミュレーションで得られたサンプル z の統計量と理論値を比較してみましょう。
# シミュレーション結果の統計量
mean_z_sim <- mean(z)
sd_z_sim <- sd(z)
# 理論値とシミュレーション結果を比較
comparison <- data.frame(
"指標" = c("平均", "標準偏差"),
"理論値" = c(mu_z_theory, sd_z_theory),
"シミュレーション結果" = c(mean_z_sim, sd_z_sim)
)
print(comparison) 指標 理論値 シミュレーション結果
1 平均 30.000000 30.025959
2 標準偏差 3.605551 3.569309数値で比較しても、シミュレーションから得られた標本平均と標本標準偏差は、理論値に近いことがわかります。サンプルサイズ n_samples を大きくすればするほど、この結果はさらに理論値に近づきます。
まとめ
このシミュレーションを通して、独立な正規分布に従う確率変数の和が、実際に再び正規分布に従うという「正規分布の再生性」を視覚的・数値的に確認することができました。この性質は、統計的推論の多くの場面で基礎となる重要な概念です。
以上です。