Rで 確率分布:スチューデントのt分布 を試みます。
本ポストはこちらの続きです。

1. スチューデントのt分布とは
スチューデントのt分布は、正規分布に従う母集団から少数の標本を抽出した際に、母分散が未知の場合に母平均を推定・検定するために用いられる連続確率分布です。正規分布と非常によく似た形状をしていますが、標本サイズが小さいことによる不確実性を考慮した形になっています。
t分布の定義
t分布の成り立ちは、標準正規分布とカイ2乗分布に基づいています。 独立な確率変数 \(Z\) と \(U\) が、それぞれ
- \(Z \sim N(0, 1)\) (標準正規分布)
- \(U \sim \chi^2(k)\) (自由度 \(k\) のカイ2乗分布)
に従うとします。このとき、以下の式で定義される確率変数 \(T\)
\[T = \dfrac{Z}{\sqrt{U/k}}\]
が従う分布が、自由度 \(k\) のt分布です。
統計学の文脈では、母平均 \(\mu\)、母分散 \(\sigma^2\) の正規分布から抽出した標本サイズ \(n\) の標本平均を \(\bar{X}\)、不偏分散を \(s^2\) とすると、統計量 \(t = \dfrac{\bar{X}-\mu}{s/\sqrt{n}}\) が自由度 \(n-1\) のt分布に従うことが知られています。これは、母分散 \(\sigma^2\) の代わりに標本から計算した不偏分散 \(s^2\) を使っている点が重要です。
確率密度関数 (Probability Density Function, PDF)
自由度 \(k\) のt分布に従う確率変数 \(T\) の確率密度関数 \(f(t)\) は、以下の式で定義されます。
\[f(t|k) = \dfrac{\Gamma(\dfrac{k+1}{2})}{\sqrt{k\pi}\Gamma(\dfrac{k}{2})} \left(1 + \dfrac{t^2}{k}\right)^{-\dfrac{k+1}{2}}\]
この分布も、カイ2乗分布と同様にただ一つのパラメータで形状が決定されます。
- \(k\): 自由度 (degrees of freedom, df)
- 分布の形状を決定する唯一のパラメータです。
- 標本から母平均を推定する場合、自由度は通常「標本サイズ - 1」(\(k = n-1\))となります。
主な特徴
- 形状: 平均0を中心に左右対称な釣鐘型をしており、標準正規分布と非常によく似ています。
- 裾の重さ: 標準正規分布と比較して、中心の山はやや低く、裾が重い(厚い)のが最大の特徴です。これは、母分散が未知であるという不確実性を反映しており、極端な値(外れ値)が出現する確率が正規分布よりも高くなっています。
- 自由度の影響:
- 自由度 \(k\) が小さいほど、裾は重くなります(分布のばらつきが大きくなる)。
- 自由度1のt分布は、標準コーシー分布と同一であり、平均や分散が定義できないほど極端に裾の重い分布となります。
- 自由度 \(k\) が大きくなるにつれて、t分布は標準正規分布 \(N(0, 1)\) に急速に収束します。経験的に、自由度が30程度を超えると、t分布は標準正規分布とほぼ同じとみなせるようになります。
- 代表値:
- 平均 (Mean): 0 (ただし、\(k>1\) の場合)
- 分散 (Variance): \(\dfrac{k}{k-2}\) (ただし、\(k>2\) の場合)。分散は常に1より大きくなります。
2. t分布の応用例
t分布は、特に標本サイズが小さい場合の統計的推測において中心的な役割を果たします。その主な応用はt検定です。
- 1標本t検定 (One-sample t-test)
- 正規分布を仮定できる1つのグループのデータから、母平均が特定の値と等しいと言えるかを検定します。
- 例: あるクラスの生徒30人の平均身長が、全国平均の170cmと有意に異なると言えるか。
- 対応のない2標本t検定 (Independent two-sample t-test)
- 互いに独立な2つのグループの母平均に差があるかを検定します。
- 例: 新しい教育法を適用したクラスと、従来の教育法のクラスで、テストの平均点に有意な差があるか。
- 対応のある2標本t検定 (Paired t-test)
- 同じ対象者に対して、何らかの介入の前と後で測定した値など、ペアになるデータの平均値に差があるかを検定します。
- 例: ある薬を投与する前と後で、患者の血圧の平均値に有意な変化があったか。
- 回帰分析
- 回帰分析で得られた各回帰係数が、統計的に有意に0と異なるかを検定するためにt分布が利用されます。
3. R言語によるシミュレーション
ここでは、自由度 \(k\) を変更した3つのt分布と、比較対象として標準正規分布を1枚のチャートに描画します。これにより、t分布の最大の特徴である「裾の重さ」と「自由度による正規分布への収束」を視覚的に理解します。
- ケース1:
自由度 k=1(コーシー分布と同一。非常に裾が重い) - ケース2:
自由度 k=3(裾が重いが、山型が明確になる) - ケース3:
自由度 k=30(標準正規分布にかなり近い) - 比較対象: 標準正規分布
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(-5, 5, length.out = 1000)
# 2. 異なる自由度を持つt分布と、標準正規分布の確率密度を計算
# t分布は dt(x, df), 正規分布は dnorm(x) を使用
df <- tibble(
x = x_vals
) %>%
mutate(
`自由度 k=1` = dt(x, df = 1),
`自由度 k=3` = dt(x, df = 3),
`自由度 k=30` = dt(x, df = 30),
`標準正規分布` = dnorm(x, mean = 0, sd = 1)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "distribution",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(distribution = factor(distribution, levels = c(
"自由度 k=1",
"自由度 k=3",
"自由度 k=30",
"標準正規分布"
)))
# 4. 各分布に割り当てる色と線種を定義
manual_colors <- c(
"自由度 k=1" = "blue",
"自由度 k=3" = "red",
"自由度 k=30" = "darkgreen",
"標準正規分布" = "black"
)
manual_linetypes <- c(
"自由度 k=1" = "solid",
"自由度 k=3" = "solid",
"自由度 k=30" = "solid",
"標準正規分布" = "dashed" # 正規分布を破線にして区別しやすくする
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = distribution, linetype = distribution)) +
geom_line(linewidth = 1.1) +
scale_color_manual(values = manual_colors) +
scale_linetype_manual(values = manual_linetypes) +
labs(
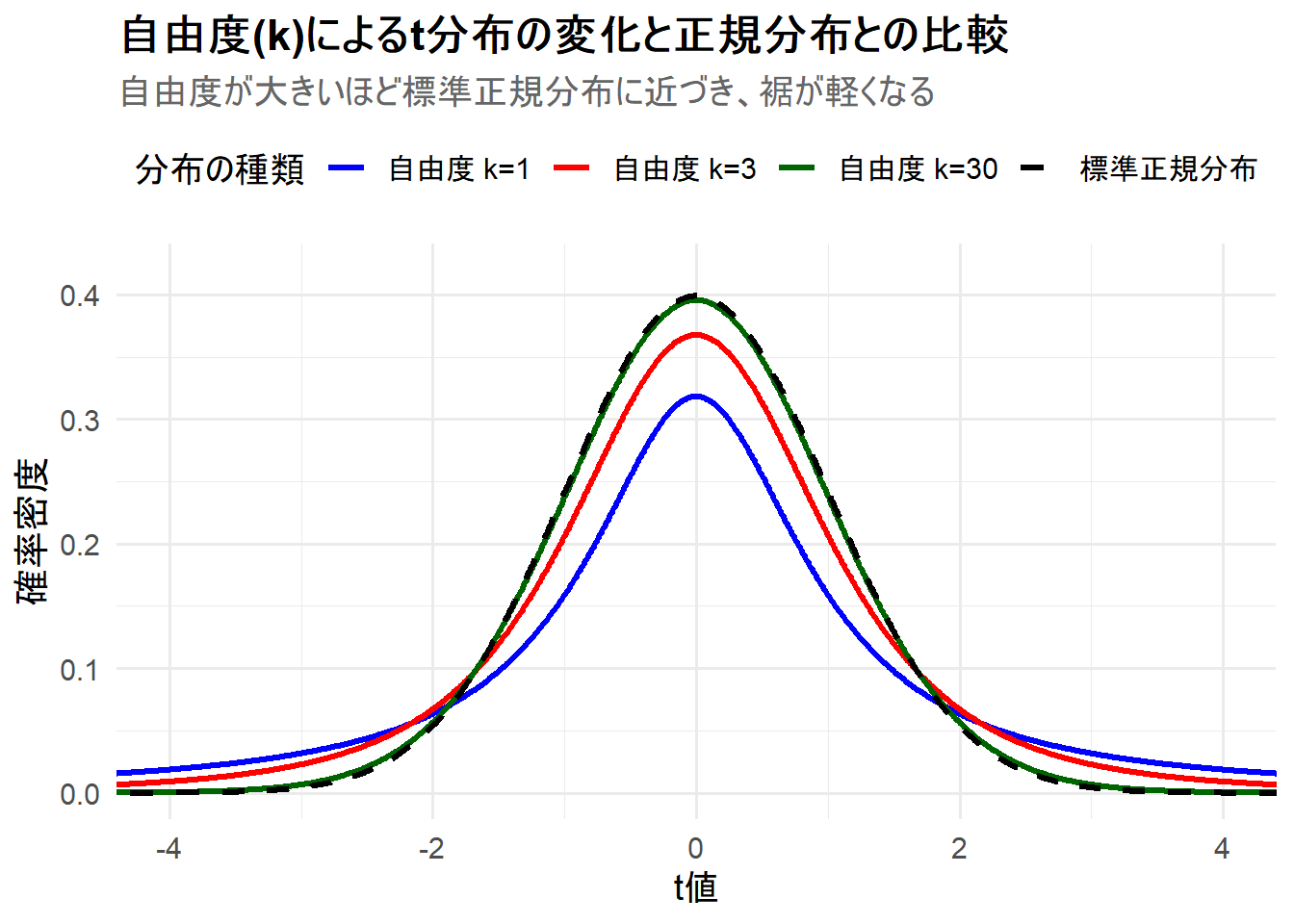
title = "自由度(k)によるt分布の変化と正規分布との比較",
subtitle = "自由度が大きいほど標準正規分布に近づき、裾が軽くなる",
x = "t値",
y = "確率密度",
color = "分布の種類",
linetype = "分布の種類"
) +
coord_cartesian(xlim = c(-4, 4), ylim = c(0, 0.42)) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのt分布と標準正規分布が描画されたチャート Figure 1 が生成されます。
-
標準正規分布(黒破線): 比較の基準となる分布です。 -
自由度 k=1(青線): コーシー分布と同一の分布です。中心での山の高さが最も低く、その一方で裾の部分(xが-3や3のあたり)の確率密度は最も高くなっています。これが「裾が重い」状態であり、極端な値が出やすいことを示しています。 -
自由度 k=3(赤線):k=1に比べると中心の山が高くなり、裾が軽くなっていますが、まだ標準正規分布よりは裾が重いことがわかります。 -
自由度 k=30(緑線): 見た目上、標準正規分布(黒破線)とほとんど重なっていることが確認できます。このように、自由度が30程度になると、t分布は実用上、標準正規分布とほぼ同じと見なすことができます。
このシミュレーションから、t分布が母分散未知という不確実性を「裾の重さ」で表現しており、自由度(標本サイズ)が大きくなるにつれてその不確実性が解消され、標準正規分布に近づいていく様子が直感的に理解できます。
4. 自由度 k=1 のt分布とコーシー分布
1. 確率密度関数(PDF)による証明
まず、両者の確率密度関数が一致することを確認します。
自由度 \(k\) のt分布のPDFは以下の通りでした。 \[f_T(t|k) = \dfrac{\Gamma(\dfrac{k+1}{2})}{\sqrt{k\pi}\Gamma(\dfrac{k}{2})} \left(1 + \dfrac{t^2}{k}\right)^{-\dfrac{k+1}{2}}\]
ここで、自由度 \(k=1\) を代入します。ガンマ関数の性質 \(\Gamma(1)=1\) と \(\Gamma(\dfrac{1}{2})=\sqrt{\pi}\) を用いると、
\[\begin{eqnarray}
f_T(t|k=1) &=& \dfrac{\Gamma(1)}{\sqrt{1\cdot\pi}\Gamma(\dfrac{1}{2})} \left(1 + t^2\right)^{-1}\\
&=& \dfrac{1}{\sqrt{\pi}\cdot\sqrt{\pi}} (1 + t^2)^{-1}\\
&=& \dfrac{1}{\pi(1+t^2)}
\end{eqnarray}\]一方、標準コーシー分布のPDFは、まさにこの形で定義されます。 \[f_C(x) = \dfrac{1}{\pi(1+x^2)}\]
このように、自由度1のt分布の確率密度関数は、標準コーシー分布の確率密度関数と一致します。
2. 確率変数の比としての定義
両分布は「2つの確率変数の比」として定義できる点でも関連しています。
- コーシー分布の定義: 独立な確率変数 \(Z_1, Z_2\) がともに標準正規分布 \(N(0,1)\) に従うとき、その比 \(X = \dfrac{Z_1}{Z_2}\) が従う分布が標準コーシー分布です。
- 自由度1のt分布の定義: 独立な確率変数 \(Z, U\) がそれぞれ \(Z \sim N(0,1)\), \(U \sim \chi^2(1)\) に従うとき、\(T = \dfrac{Z}{\sqrt{U/1}}\) が自由度1のt分布に従います。 ここで、自由度1のカイ2乗分布 \(\chi^2(1)\) とは、標準正規分布に従う確率変数 \(Z_2\) を2乗したもの、すなわち \(U=Z_2^2\) と定義されます。 したがって、 \[T = \dfrac{Z}{\sqrt{Z_2^2}} = \dfrac{Z}{|Z_2|}\] となります。
\(Z_2\) と \(|Z_2|\) の分布は異なりますが、\(Z_1/Z_2\) と \(Z/|Z_2|\) が同じ分布(コーシー分布)に従うことが証明されています。直感的には、\(Z_2\) の符号が反転しても、比の分布の対称性から全体としては同じ形状になる、と理解できます。
3. コーシー分布の特異性とt分布の関係
この関係性は、t分布が自由度が小さい場合に持つ「裾の重さ」を理解する上で非常に重要です。コーシー分布は、以下のような特異な性質を持つことで知られています。
- 平均や分散(高次のモーメント)が定義できない: グラフを見ても分かる通り、裾が非常に重く、積分が発散してしまうため、期待値を計算できません。
t分布の性質を思い出してみると、
- 平均が定義できるのは、自由度 \(k > 1\) のとき
- 分散が定義できるのは、自由度 \(k > 2\) のとき
でした。
自由度1のt分布がコーシー分布と同一であることは、なぜ \(k=1\) のときに平均や分散が定義できないのかを説明してくれます。
以上です。