Rで確率分布:ワイブル分布

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 2.5, length.out = 1000)

# 2. 異なるパラメータを持つワイブル分布の確率密度を計算
# dweibull(x, shape, scale) を使用。shapeが形状k, scaleが尺度λ
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `k=0.7 (初期故障型)` = dweibull(x, shape = 0.7, scale = 1),
    `k=1.0 (偶発故障型)` = dweibull(x, shape = 1.0, scale = 1),
    `k=2.0 (摩耗故障型)` = dweibull(x, shape = 2.0, scale = 1),
    `k=5.0 (摩耗故障型)` = dweibull(x, shape = 5.0, scale = 1)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "k=0.7 (初期故障型)",
    "k=1.0 (偶発故障型)",
    "k=2.0 (摩耗故障型)",
    "k=5.0 (摩耗故障型)"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  `k=0.7 (初期故障型)` = "blue",
  `k=1.0 (偶発故障型)` = "red",
  `k=2.0 (摩耗故障型)` = "darkgreen",
  `k=5.0 (摩耗故障型)` = "purple"
)

# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  geom_line(linewidth = 1.2) +
  scale_color_manual(values = manual_colors) +
  labs(
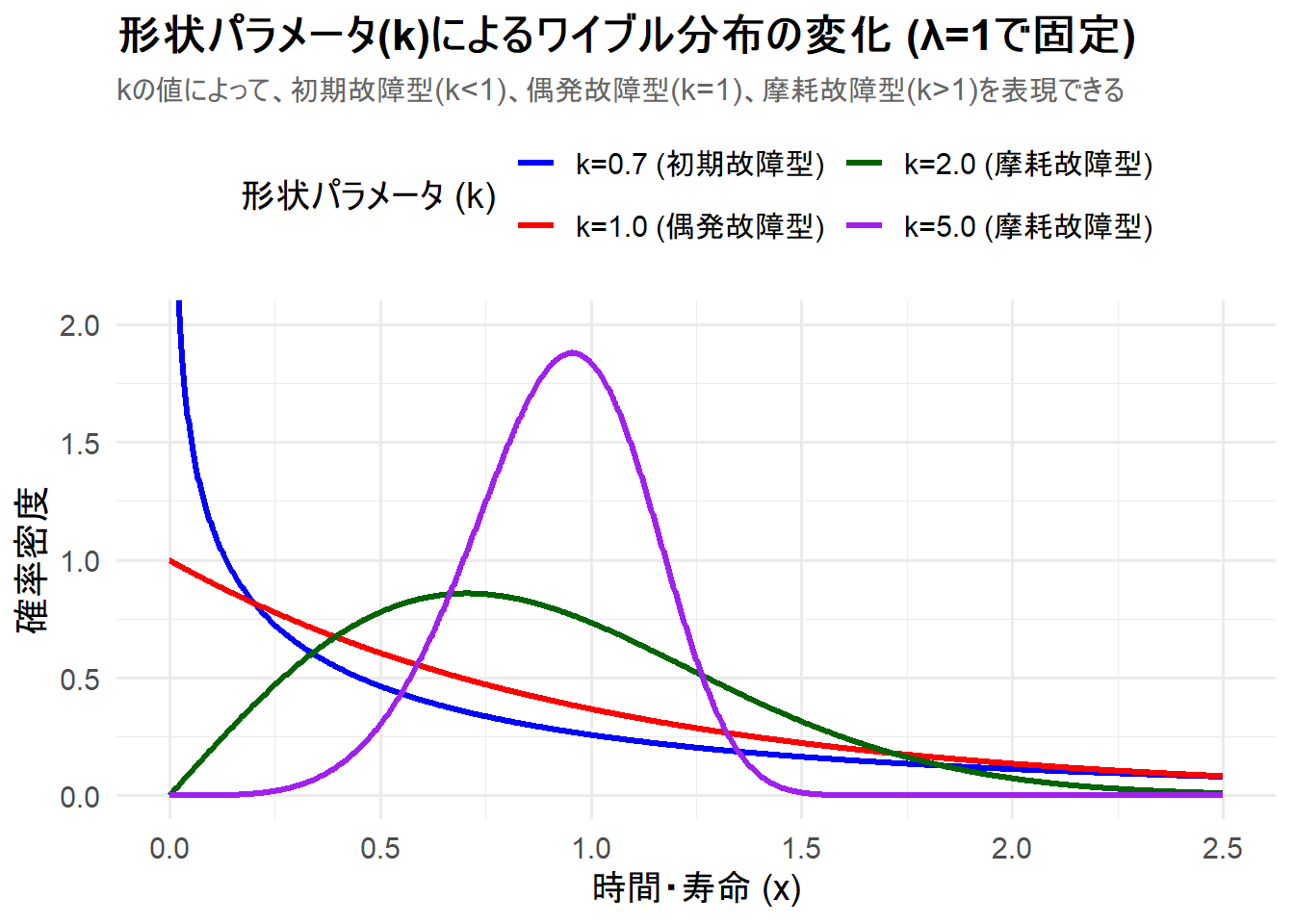
    title = "形状パラメータ(k)によるワイブル分布の変化 (λ=1で固定)",
    subtitle = "kの値によって、初期故障型(k<1)、偶発故障型(k=1)、摩耗故障型(k>1)を表現できる",
    x = "時間・寿命 (x)",
    y = "確率密度",
    color = "形状パラメータ (k)"
  ) +
  coord_cartesian(ylim = c(0, 2.0)) + # y軸の範囲を調整
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "top",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40", size = 12)
  ) +
  guides(color = guide_legend(nrow = 2))

# チャートの表示
print(p)

seed <- 20250809
set.seed(seed)

library(ggplot2)
library(patchwork)

alpha <- 2
beta <- 5
Nsim <- 10000
n_list <- c(10, 100, 1000)

# 最大値（有限上限→逆ワイブル→ワイブル正規化）
make_plot_max <- function(n, alpha, beta, Nsim) {
  max_vals <- replicate(Nsim, max(rbeta(n, alpha, beta)))
  B_ab <- beta(alpha, beta)
  C_max <- 1 / (beta * B_ab)
  b_n <- (n * C_max)^(-1 / beta)
  T_vals <- (1 - max_vals) / b_n
  df <- data.frame(T = T_vals)
  ggplot(df, aes(x = T)) +
    geom_histogram(aes(y = ..density..), bins = 50, fill = "lightblue", color = "white") +
    stat_function(
      fun = function(x) dweibull(x, shape = beta, scale = 1),
      linewidth = 1.2, color = "red"
    ) +
    labs(
      title = paste0("Max: n = ", n),
      x = expression(T == (1 - M[n]) / b[n]),
      y = "Density"
    ) +
    theme_minimal()
}

# 最小値（有限下限→ワイブル）
make_plot_min <- function(n, alpha, beta, Nsim) {
  min_vals <- replicate(Nsim, min(rbeta(n, alpha, beta)))
  B_ab <- beta(alpha, beta)
  C_min <- 1 / (alpha * B_ab)
  a_n <- (n * C_min)^(-1 / alpha)
  T_vals <- min_vals / a_n
  df <- data.frame(T = T_vals)
  ggplot(df, aes(x = T)) +
    geom_histogram(aes(y = ..density..), bins = 50, fill = "lightgreen", color = "white") +
    stat_function(
      fun = function(x) dweibull(x, shape = alpha, scale = 1),
      linewidth = 1.2, color = "red"
    ) +
    labs(
      title = paste0("Min: n = ", n),
      x = expression(T == m[n] / a[n]),
      y = "Density"
    ) +
    theme_minimal()
}

# プロットを並べる
plots_max <- lapply(n_list, make_plot_max, alpha = alpha, beta = beta, Nsim = Nsim)
plots_min <- lapply(n_list, make_plot_min, alpha = alpha, beta = beta, Nsim = Nsim)

# patchworkで結合（上段=最大値, 下段=最小値）
(patchwork::wrap_plots(plots_max, nrow = 1) /
  patchwork::wrap_plots(plots_min, nrow = 1)) +
  plot_annotation(
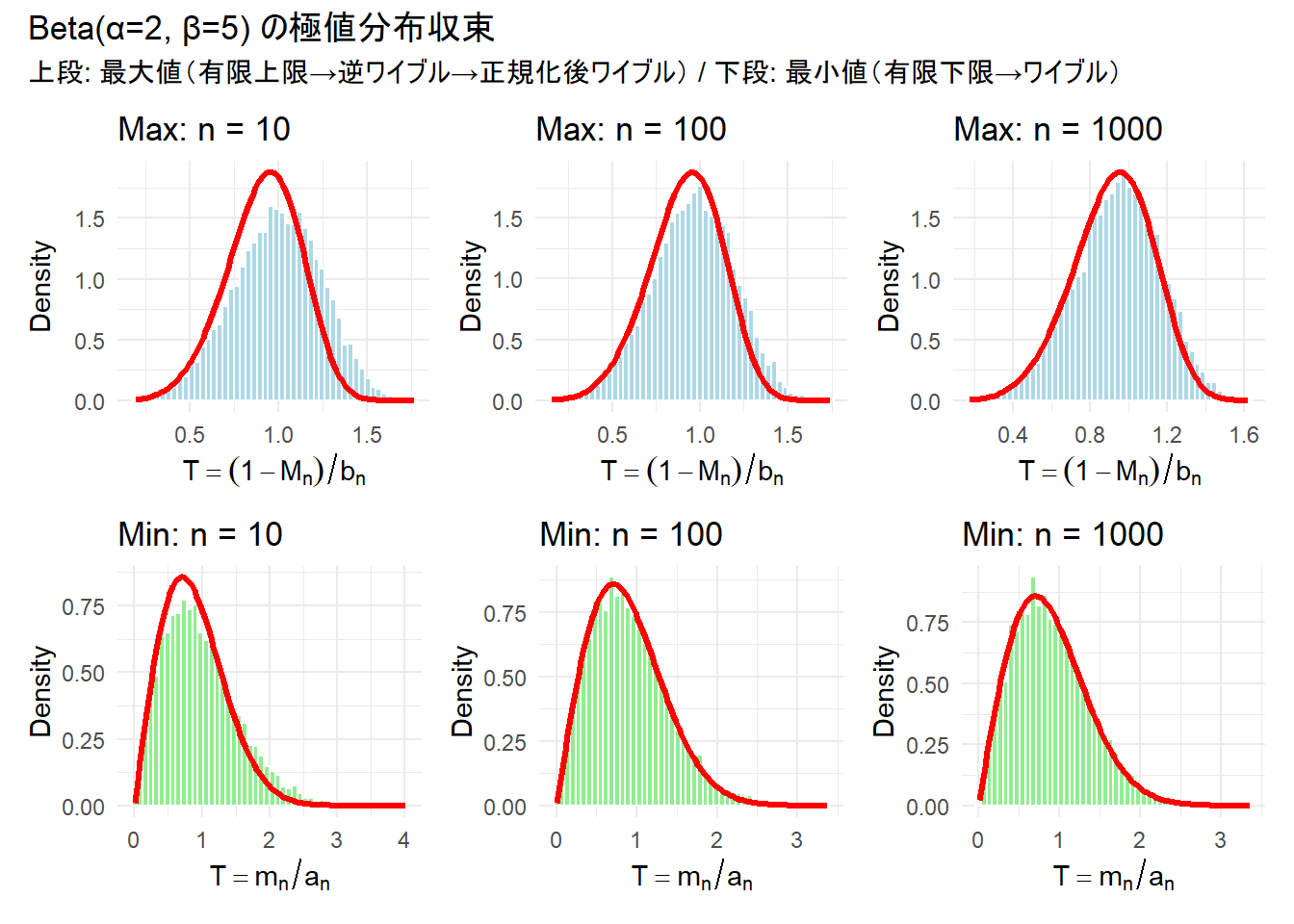
    title = "Beta(α=2, β=5) の極値分布収束",
    subtitle = "上段: 最大値（有限上限→逆ワイブル→正規化後ワイブル） / 下段: 最小値（有限下限→ワイブル）"
  )

set.seed(seed)

# alpha <- 2
# beta  <- 5
# Nsim  <- 10000
# n_list <- c(10, 100, 10000)

# Q–Qプロット作成関数
make_qq_max <- function(n, alpha, beta, Nsim) {
  max_vals <- replicate(Nsim, max(rbeta(n, alpha, beta)))
  B_ab <- beta(alpha, beta)
  C_max <- 1 / (beta * B_ab)
  b_n <- (n * C_max)^(-1 / beta)
  T_vals <- (1 - max_vals) / b_n

  # 理論分布のquantile
  probs <- ppoints(length(T_vals))
  theo_q <- qweibull(probs, shape = beta, scale = 1)
  emp_q <- quantile(T_vals, probs)

  df <- data.frame(emp = emp_q, theo = theo_q)
  ggplot(df, aes(x = theo, y = emp)) +
    geom_point(alpha = 0.5, color = "blue") +
    geom_abline(slope = 1, intercept = 0, color = "red", linewidth = 1) +
    labs(
      title = paste0("Max: n = ", n),
      x = "Theoretical Quantiles (Weibull)",
      y = "Empirical Quantiles"
    ) +
    theme_minimal() +
    theme(axis.title = element_text(size = 10))
}

make_qq_min <- function(n, alpha, beta, Nsim) {
  min_vals <- replicate(Nsim, min(rbeta(n, alpha, beta)))
  B_ab <- beta(alpha, beta)
  C_min <- 1 / (alpha * B_ab)
  a_n <- (n * C_min)^(-1 / alpha)
  T_vals <- min_vals / a_n

  probs <- ppoints(length(T_vals))
  theo_q <- qweibull(probs, shape = alpha, scale = 1)
  emp_q <- quantile(T_vals, probs)

  df <- data.frame(emp = emp_q, theo = theo_q)
  ggplot(df, aes(x = theo, y = emp)) +
    geom_point(alpha = 0.5, color = "darkgreen") +
    geom_abline(slope = 1, intercept = 0, color = "red", linewidth = 1) +
    labs(
      title = paste0("Min: n = ", n),
      x = "Theoretical Quantiles (Weibull)",
      y = "Empirical Quantiles"
    ) +
    theme_minimal() +
    theme(axis.title = element_text(size = 10))
}

# 各nのQ–Qプロット
plots_max_qq <- lapply(n_list, make_qq_max, alpha = alpha, beta = beta, Nsim = Nsim)
plots_min_qq <- lapply(n_list, make_qq_min, alpha = alpha, beta = beta, Nsim = Nsim)

# 並べて表示（上段=最大値, 下段=最小値）
(patchwork::wrap_plots(plots_max_qq, nrow = 1) /
  patchwork::wrap_plots(plots_min_qq, nrow = 1)) +
  plot_annotation(
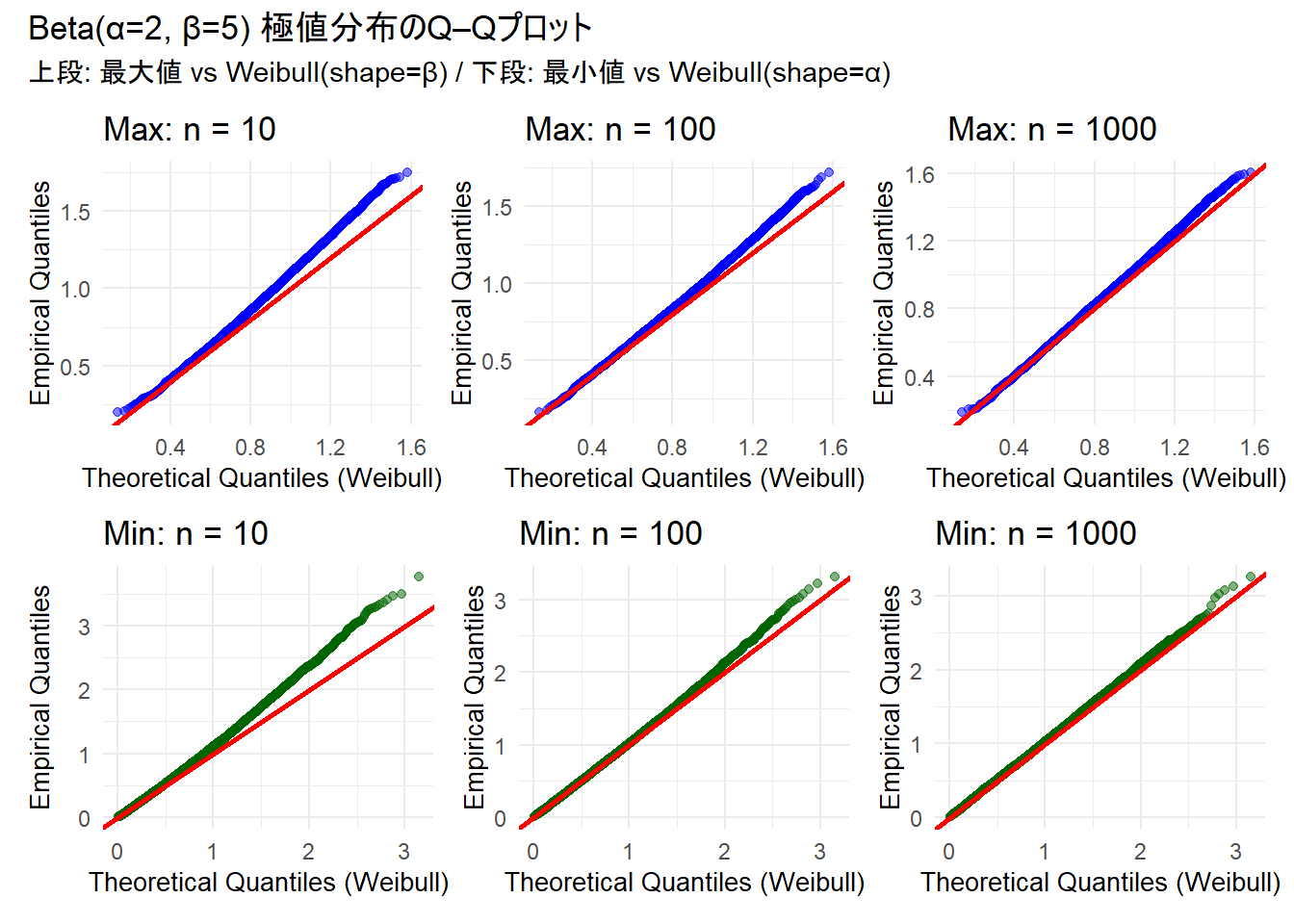
    title = "Beta(α=2, β=5) 極値分布のQ–Qプロット",
    subtitle = "上段: 最大値 vs Weibull(shape=β) / 下段: 最小値 vs Weibull(shape=α)"
  )