Rで確率分布:多次元正規分布

確率密度関数 (Probability Density Function, PDF)

\(k\)次元の確率変数ベクトル \(\mathbf{x} = (x_1, x_2, \dots, x_k)^\mathrm{T}\) が多次元正規分布に従うとき、その確率密度関数は以下の式で定義されます。

\[f(\mathbf{x} | \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \dfrac{1}{(2\pi)^{k/2} |\boldsymbol{\Sigma}|^{1/2}} \exp\left(-\dfrac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^\mathrm{T} \boldsymbol{\Sigma}^{-1} (\mathbf{x}-\boldsymbol{\mu})\right)\]

この分布は、2つのパラメータ（ベクトルと行列）によって決定されます。

• \(\boldsymbol{\mu}\) (ミュー): 平均ベクトル (Mean Vector)
  • 各確率変数 \(x_i\) の平均値 \(\mu_i\) を要素に持つ \(k\)次元のベクトルです。
  • \(\boldsymbol{\mu} = E[\mathbf{x}] = (\mu_1, \mu_2, \dots, \mu_k)^\mathrm{T}\)
  • このベクトルは、分布の中心（最も確率密度が高い点）の位置を決定します。
• \(\boldsymbol{\Sigma}\) (シグマ): 共分散行列 (Covariance Matrix)
  • 分布の広がりと形状（向き）を決定する \(k \times k\) の対称行列です。
  • 対角成分 (\(\Sigma_{ii}\)): 各確率変数 \(x_i\) の分散を表します。値が大きいほど、その変数のばらつきが大きくなります。
  • 非対角成分 (\(\Sigma_{ij}\)): 確率変数 \(x_i\) と \(x_j\) の共分散を表します。
    • \(\Sigma_{ij} > 0\): 2つの変数には正の相関があり、一方が増加するともう一方も増加する傾向があります。
    • \(\Sigma_{ij} < 0\): 2つの変数には負の相関があり、一方が増加するともう一方は減少する傾向があります。
    • \(\Sigma_{ij} = 0\): 2つの変数には相関がありません。

主な特徴

• 形状: 2次元の場合、確率密度の等高線は楕円形になります。共分散行列が単位行列のスカラー倍の場合（相関がなく、各変数の分散が等しい場合）、等高線は真円になります。
• 周辺分布: 多次元正規分布の各変数（またはその一部）の周辺分布は、それ自身も正規分布に従います。
• 独立との関係: 多次元正規分布においては、「相関がないこと（共分散が0）」と「確率的に独立であること」が同値になります。これは一般の分布では必ずしも成り立たない、正規分布の非常に重要な特性です。
  • 例：\(X \sim U[-1,1]\)、\(Y = X^2\) の場合、\(\mathrm{Cov}(X,Y)=0\) ですが、\(X\) と \(Y\) は明らかに独立ではありません。
  • \(\mathrm{Cov}(X, Y) = E[XY] - E[X]E[Y]\)
  • \(E[X] = 0\)
  • \(E[Y] = E[X^2] = 1/3\)
  • \(E[XY] = E[X^3] = 0\)
  • \(\mathrm{Cov}(X,Y) = 0 - 0 \times (1/3) = 0\)
• 線形変換の再生性: 多次元正規分布に従う確率変数ベクトルに線形変換を施した結果もまた、多次元正規分布に従います。

Rコード

# 必要なライブラリを読み込みます
library(mvtnorm)
library(ggplot2)
library(dplyr)

# 1. 描画範囲となるx1, x2軸のグリッドを生成
grid <- expand.grid(
  x1 = seq(-5, 8, length.out = 100),
  x2 = seq(-5, 8, length.out = 100)
)

# 2. 各ケースのパラメータを定義
params <- list(
  "ケース1: 無相関 (Σ_11=1, Σ_22=1, Σ_12=0)" = list(
    mu = c(0, 0),
    sigma = matrix(c(1, 0, 0, 1), nrow = 2)
  ),
  "ケース2: 正の相関 (Σ_12 = 0.8)" = list(
    mu = c(0, 0),
    sigma = matrix(c(1, 0.8, 0.8, 1), nrow = 2)
  ),
  "ケース3: 負の相関 (Σ_12 = -0.8)" = list(
    mu = c(0, 0),
    sigma = matrix(c(1, -0.8, -0.8, 1), nrow = 2)
  ),
  "ケース4: 異なる分散・中心移動 (μ=(3,2))" = list(
    mu = c(3, 2),
    sigma = matrix(c(3, 0.5, 0.5, 1), nrow = 2)
  )
)

# 3. 各グリッド点で、各ケースの確率密度を計算
# dmvnorm(x, mean, sigma) を使用
df <- params %>%
  # 各ケースに対して計算を実行
  lapply(function(p) {
    density <- dmvnorm(grid, mean = p$mu, sigma = p$sigma)
    # 元のグリッドと密度を結合
    data.frame(grid, density)
  }) %>%
  # リストを一つのデータフレームに結合し、ケース名を列として追加
  bind_rows(.id = "case")

# 4. ggplotを使用してチャートを描画 (ファセットで分割)
p <- ggplot(df, aes(x = x1, y = x2, z = density, color = ..level..)) +
  # 等高線プロットを追加
  geom_contour() +
  # ケースごとにプロットを分割
  facet_wrap(~case, ncol = 2) +
  labs(
    title = "パラメータによる2次元正規分布の変化",
    subtitle = "共分散行列(Σ)は分布の形状と向き、平均ベクトル(μ)は中心位置を決定する",
    x = "x1",
    y = "x2",
    color = "確率密度"
  ) +
  coord_fixed(ratio = 1) + # x軸とy軸のスケールを1:1に保つ
  theme_minimal(base_size = 12) +
  theme(
    legend.position = "right",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
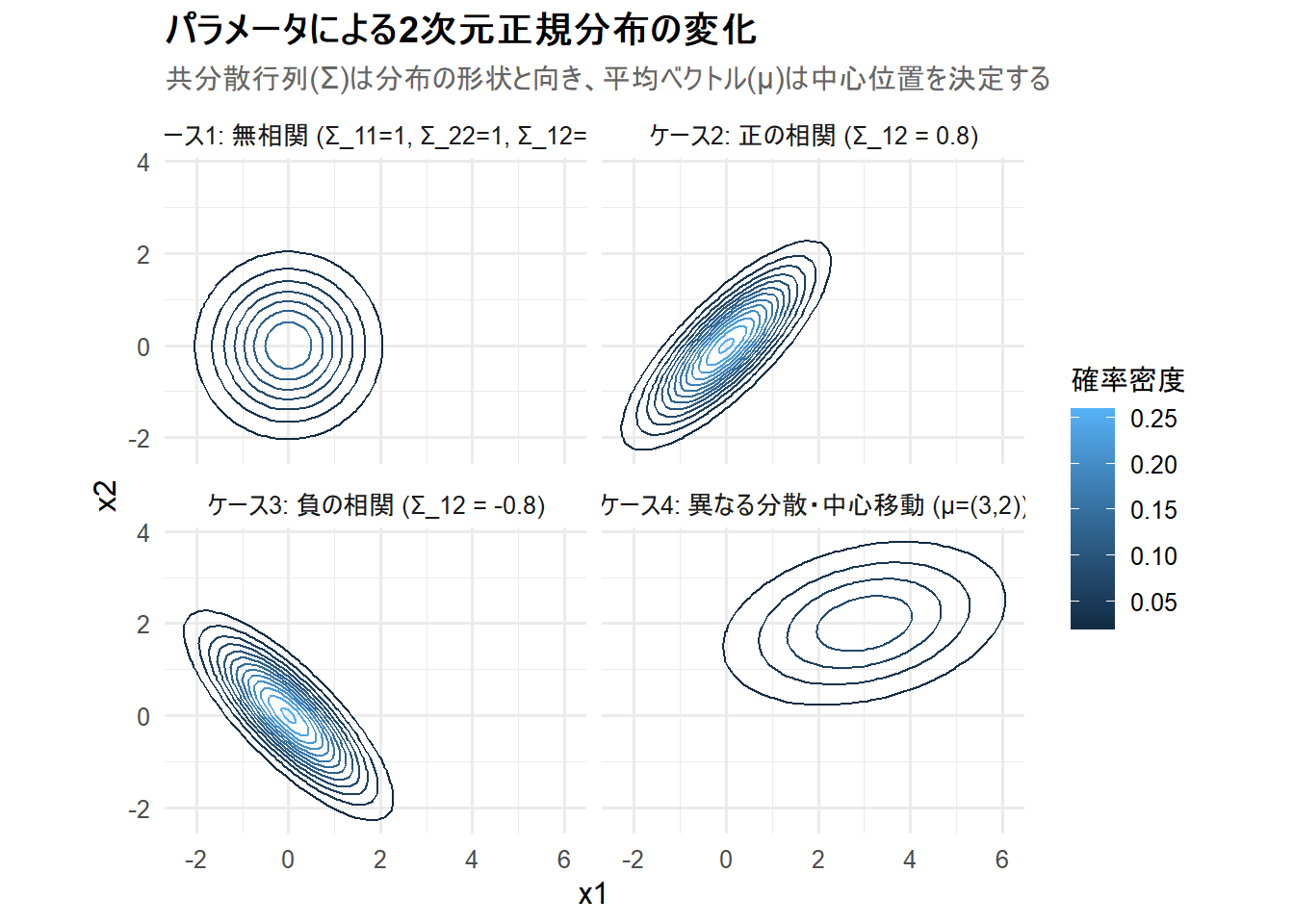
print(p)

Figure 1 の解説

上記のRコードを実行すると、4つの2次元正規分布が等高線で描画されたチャート Figure 1 が生成されます。

• ケース1: 無相関: 共分散（非対角成分）が0で、各変数の分散が等しいため、等高線は真円になっています。これは変数x1とx2が独立であることを示しています。
• ケース2: 正の相関: 共分散が正（0.8）であるため、等高線は右肩上がりの楕円になっています。これは、x1が大きい値をとるとき、x2も大きい値をとる傾向があることを示しています。
• ケース3: 負の相関: 共分散が負（-0.8）であるため、等高線は右肩下がりの楕円になっています。これは、x1が大きい値をとるとき、x2は小さい値をとる傾向があることを示しています。
• ケース4: 異なる分散・中心移動: 平均ベクトルが(3, 2)に設定されているため、分布の中心がその点に移動しています。また、x1の分散が3、x2の分散が1であるため、楕円がx1軸方向により長く伸びていることがわかります。