Rで 確率分布:対数正規分布 を試みます。
本ポストはこちらの続きです。

Rで確率分布:正規分布
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
1. 対数正規分布とは
対数正規分布(Log-normal Distribution)は、確率変数の対数をとったものが正規分布に従うような、連続確率分布です。言い換えると、確率変数 \(Y\) が正規分布 \(N(\mu, \sigma^2)\) に従うとき、 \(X = e^Y\) が従う分布が対数正規分布です。
この分布は、その値が常に正の値をとる変数(例:所得、株価、生物の個体サイズなど)をモデル化するのに適しています。
同じく常に正の値をとるガンマ分布との比較
- 生成過程の理論的背景
- 対数正規分布: 変数の変動が乗法的なプロセスで生じると考えられる場合に適します。これは、多数の独立した小さな要因が掛け算で影響し合うような状況です。例えば、資産価格が日々ランダムな「比率」で変動したり、生物の細胞が分裂・成長したりするプロセスです。このような変数の対数をとると加法的なプロセスになり、中心極限定理によって正規分布に近づくため、理論的な妥当性が高くなります。
- ガンマ分布: 変数が加法的なプロセスで生じると考えられる場合に適します。特に、指数分布に従う事象が複数回発生するまでの「待ち時間」の合計を表すモデルとして利用されます。例えば、一定の確率で発生するサーバーの故障が、k回発生するまでの時間などが該当します。
- 裾の重さ
- 一般的に、対数正規分布の方がガンマ分布よりも裾が重い傾向があります。これは、非常に大きな値(外れ値)が観測される頻度が相対的に高いことを意味します。所得分布や保険金の請求額など、極端に大きな値が時折現れるようなデータをモデル化する際には、対数正規分布の方がフィットしやすい場合があります。
- パラメータの解釈性
- 対数正規分布: パラメータの \(\mu\) と \(\sigma\) は、データを対数変換した後の正規分布の平均と標準偏差に直接対応します。このため、データを対数変換して正規分布に見えるかを確認し、その平均と標準偏差を推定するという直感的なアプローチが可能です。
- ガンマ分布: パラメータである形状母数 (\(k\)) と尺度母数 (\(\theta\)) は、待ち時間の文脈では解釈しやすいですが、それ以外の文脈では物理的な意味が直感的に分かりにくい場合があります。
| 比較項目 | 対数正規分布 | ガンマ分布 |
|---|---|---|
| 理論的背景 | 乗法的なプロセス(独立要因の積) | 加法的なプロセス(指数分布の和) |
| 主な応用 | 資産価格、所得分布、生物のサイズ | 待ち時間、故障間隔、降水量 |
| 裾の重さ | より重い傾向(極端な値が多い) | より軽い傾向 |
| パラメータ | 対数変換後の平均・標準偏差で解釈 | 形状母数と尺度母数で解釈 |
確率密度関数 (Probability Density Function, PDF)
対数正規分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、以下の式で定義されます。
\[f(x | \mu, \sigma^2) = \dfrac{1}{x\sqrt{2\pi\sigma^2}} e^{-\dfrac{(\ln(x)-\mu)^2}{2\sigma^2}} \quad (x > 0)\]
この関数も2つのパラメータによって形状が決定されますが、その解釈には注意が必要です。
- \(\mu\) (ミュー): 対数の平均 (meanlog)
- これは確率変数 \(X\) そのものの平均ではありません。\(X\) の自然対数 \(\ln(X)\) をとった時の、正規分布の平均です。この値は、対数正規分布の位置とスケール(尺度)の両方に影響を与えます。
- \(\sigma^2\) (シグマ二乗): 対数の分散 (variancelog)
- 同様に、\(X\) そのものの分散ではなく、\(\ln(X)\) をとった時の、正規分布の分散です。\(\sigma\) は対数の標準偏差 (sdlog) であり、主に対数正規分布の形状の歪み具合を決定します。
主な特徴
- 定義域: 確率変数 \(X\) は常に正の値 (\(x>0\)) をとります。グラフは \(x=0\) より右側にのみ描かれます。
- 形状: 正規分布のような対称な釣鐘型ではなく、右に長く裾を引く非対称な形状(右に歪んだ分布)をしています。
- 代表値: 平均値、中央値、最頻値は一致せず、一般的に以下の大小関係が成り立ちます。
- 最頻値 (Mode): \(e^{\mu - \sigma^2}\)
- 中央値 (Median): \(e^{\mu}\)
- 平均値 (Mean): \(e^{\mu + \sigma^2/2}\)
この関係から、最頻値 < 中央値 < 平均値 となります。
- 生成過程: 正規分布が「加法的なプロセス」(多くの独立した要因の和)の結果として現れるのに対し、対数正規分布は「乗法的なプロセス」(多くの独立した要因の積)の結果として現れる事象のモデルとして用いられます。例えば、ある資産価格が日々ランダムな倍率で変動する場合、その将来価格は対数正規分布でモデル化できます。
2. 対数正規分布の応用例
値が正に限定され、乗法的なプロセスによって変動する多くの事象が対数正規分布でモデル化されます。
- 経済学・金融工学
- 所得分布・資産分布: 一部の人々が非常に高い所得を持つという、右に裾の長い分布を表現します(パレート分布でモデル化されることもあります)。
- 株価・資産価格: 株価は負になることがなく、その変動は現在の価格に対する比率(例: 前日比+1%)で考えられることが多いため、基本的なモデルとして対数正規分布が用いられます(ブラック-ショールズモデルの基礎)。
- 生物学・医学
- 生物の個体サイズ: ある種の生物の成体重量など、成長が乗法的なプロセスで進むと考えられる場合に適用されます。
- 潜伏期間: 感染症が発症するまでの潜伏期間が、対数正規分布に従うとされることがあります。
- 信頼性工学
- 故障寿命: 電子部品などの製品が故障するまでの時間は、多くの微小な劣化要因が乗法的に蓄積した結果と考えることができ、対数正規分布でモデル化されることがあります。
3. R言語によるシミュレーション
ここでは、パラメータ(対数の平均 \(\mu\) と対数の標準偏差 \(\sigma\))を変更した4つの対数正規分布を、1枚のチャートにggplot2を用いて描画します。
- ケース1:
μ=0, σ=0.25(σが小さく、比較的対称に近い形状) - ケース2:
μ=0, σ=0.5(σが大きくなり、歪みが強くなる) - ケース3:
μ=0, σ=1.0(σがさらに大きくなり、歪みが非常に顕著になる) - ケース4:
μ=1.5, σ=0.5(μが大きくなり、分布全体が右にシフトしスケールが大きくなる)
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成 (対数正規分布は x > 0)
x_vals <- seq(0.01, 20, length.out = 1000)
# 2. 4つの異なるパラメータを持つ対数正規分布の確率密度を計算
# dlnorm(x, meanlog, sdlog) を使用
df <- tibble(
x = x_vals
) %>%
mutate(
`μ=0, σ=0.25` = dlnorm(x, meanlog = 0, sdlog = 0.25),
`μ=0, σ=0.5` = dlnorm(x, meanlog = 0, sdlog = 0.5),
`μ=0, σ=1.0` = dlnorm(x, meanlog = 0, sdlog = 1.0),
`μ=1.5, σ=0.5` = dlnorm(x, meanlog = 1.5, sdlog = 0.5)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
mutate(parameters = factor(parameters, levels = c(
"μ=0, σ=0.25",
"μ=0, σ=0.5",
"μ=0, σ=1.0",
"μ=1.5, σ=0.5"
)))
# 4. 各パラメータに割り当てる色を名前付きベクトルで定義
manual_colors <- c(
"μ=0, σ=0.25" = "blue",
"μ=0, σ=0.5" = "red",
"μ=0, σ=1.0" = "darkgreen",
"μ=1.5, σ=0.5" = "purple"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
labs(
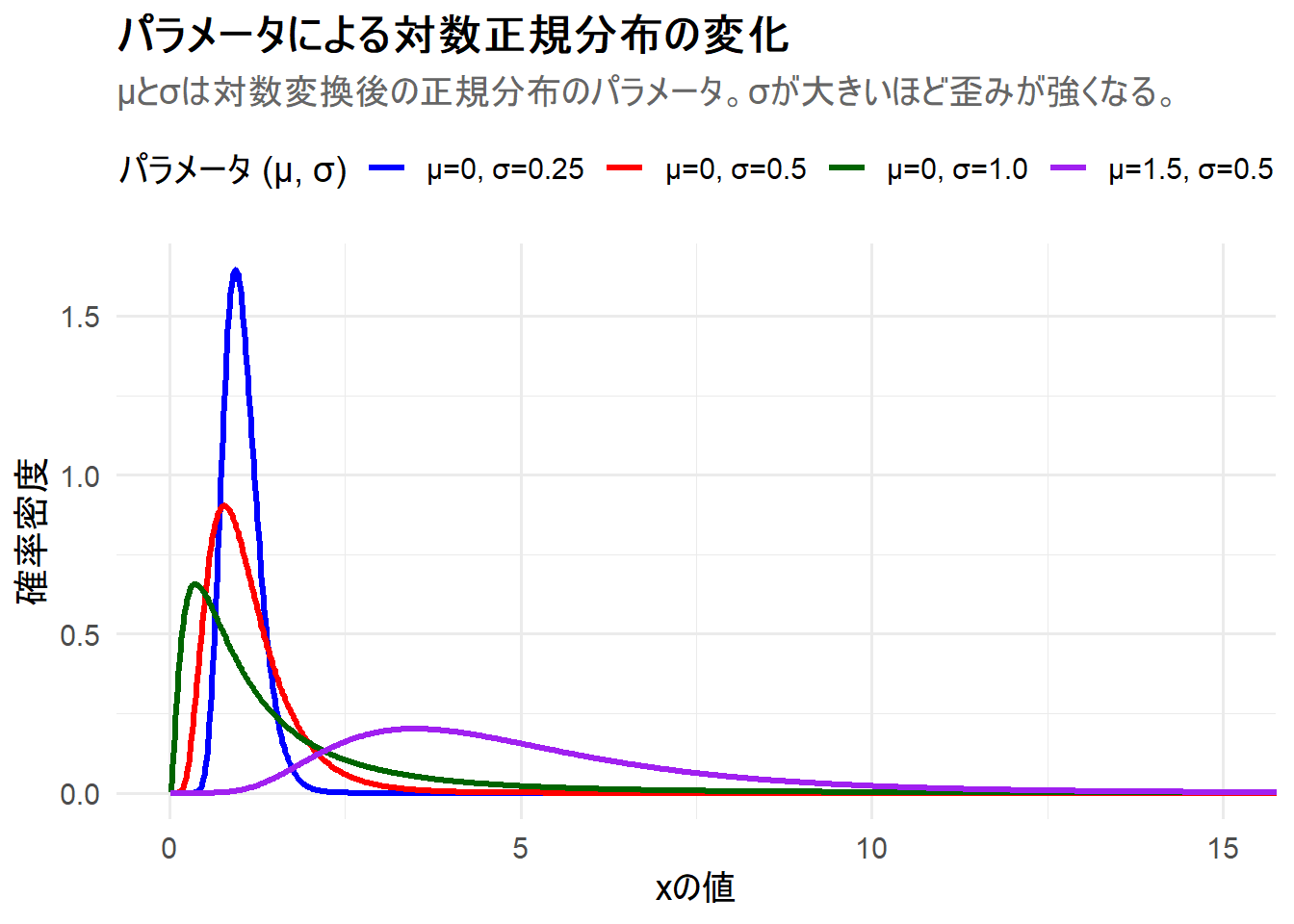
title = "パラメータによる対数正規分布の変化",
subtitle = "μとσは対数変換後の正規分布のパラメータ。σが大きいほど歪みが強くなる。",
x = "xの値",
y = "確率密度",
color = "パラメータ (μ, σ)"
) +
# x軸の範囲を調整して、分布の形状を分かりやすくする
coord_cartesian(xlim = c(0, 15)) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、4つの対数正規分布が描画されたチャート Figure 1 が生成されます。
-
μ=0, σ=0.25(青線): 対数の標準偏差 \(\sigma\) が小さいため、歪みは比較的小さく、鋭いピークを持っています。 -
μ=0, σ=0.5(赤線): \(\sigma\) が大きくなったことで、分布の歪みが強くなっています。青線に比べてピークが左に寄り、右側の裾が長くなっているのがわかります。 -
μ=0, σ=1.0(緑線): \(\sigma\) がさらに大きくなり、歪みが非常に顕著になっています。ピークはさらに左に寄って低くなり、右に非常に長い裾を引く分布となっています。所得分布など、極端な値をとる少数のデータを含むような現象のモデルに近い形です。 -
μ=1.5, σ=0.5(紫線): 赤線(μ=0, σ=0.5)と比較して、対数標準偏差σは同じですが、対数平均μが0から1.5へと大きくなっています。μは分布のスケール(尺度)に影響するため、ピークの位置が右に移動すると同時に、分布の分散も大きくなります。その結果、山の高さは低く、より広く裾を引いた形状に変化していることが確認できます。
以上です。