Rで確率分布:指数分布

Rで 確率分布:指数分布 を試みます。

本ポストはこちらの続きです。

const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...

1. 指数分布とは

指数分布（Exponential Distribution）は、あるランダムなイベントが発生するまでの「時間」や「間隔」をモデル化するために用いられる連続確率分布です。例えば、「次に客が来るまでの時間」、「製品が故障するまでの寿命」、「電話がかかってくるまでの時間」などが、指数分布に従う典型的な例です。

確率密度関数 (Probability Density Function, PDF)

指数分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、以下の式で定義されます。

\[f(x | \lambda) = \lambda e^{-\lambda x} \quad (x \ge 0)\]

この分布は、ただ一つのパラメータによってその形状が決定されます。

\(\lambda\) (ラムダ): レートパラメータ (rate parameter)
- 単位時間あたりにイベントが発生する平均回数を表します。
- \(\lambda\) が大きいほど、イベントが頻繁に発生することを意味し、待ち時間は短くなる傾向があります。
- \(\lambda\) が小さいほど、イベントが稀にしか発生しないことを意味し、待ち時間は長くなる傾向があります。

主な特徴

定義域: 確率変数は常に非負の値 (\(x \ge 0\)) をとります。
形状: \(x=0\) で最大値をとり、その後、文字通り指数関数的に単調減少する、右に長く裾を引く形状をしています。
無記憶性: 指数分布を特徴づける性質です。これは、「ある時点まで待ったという事実は、その後の待ち時間に影響を与えない」ということを意味します。
- 数式で表すと、\(P(X > t+s | X > t) = P(X > s)\) となります。
- 例: ある電球の寿命が指数分布に従うとします。「この電球が100時間切れていない」という事実がわかった上で、「これからさらに50時間以上もつ確率」は、「新品の電球が最初から50時間以上もつ確率」と全く同じです。つまり、電球は過去の稼働時間を「記憶」しておらず、常に新品同様であると仮定されます。これは連続確率分布では指数分布だけが持つ性質です。
代表値:
- 平均 (Mean): \(E[X] = \dfrac{1}{\lambda}\)
- 分散 (Variance): \(V[X] = \dfrac{1}{\lambda^2}\)
平均がレートパラメータの逆数であることは直感的です。例えば、単位時間あたり平均2回（\(\lambda=2\)）イベントが起こるなら、次のイベントまでの平均待ち時間は1/2時間となります。
他の分布との関係:
- ポアソン分布: 「単位時間あたりのイベント発生回数」がポアソン分布に従うとき、そのイベントの「発生間隔」は指数分布に従います。
- ガンマ分布: 指数分布は、ガンマ分布の形状パラメータを1としたケースです。
- カイ2乗分布: 自由度2の中心カイ2乗分布は、レートパラメータ \(\lambda=1/2\) の指数分布と一致します。

2. 指数分布の応用例

無記憶性という仮定が成り立つ、あるいは近似できる多くの現象に適用されます。

信頼性工学・品質管理
- 電子部品など、摩耗による劣化がなく、突発的に故障するような製品の寿命のモデル化に用いられます。
待ち行列理論
- 銀行の窓口やスーパーのレジ、コールセンターなどへの顧客の到着間隔や、サーバへのリクエストの到着間隔をモデル化するのに使われます。これはシステム性能を評価する上で基本となります。
物理学
- 放射性原子が崩壊するまでの時間をモデル化します。原子の崩壊は過去の経過時間とは無関係に、一定の確率で発生するため、無記憶性が成り立ちます。
金融工学
- 企業が債務不履行（デフォルト）を起こすまでの時間（生存期間）をモデル化する、クレジットリスクモデルの基本的な要素として利用されることがあります。

3. R言語によるシミュレーション

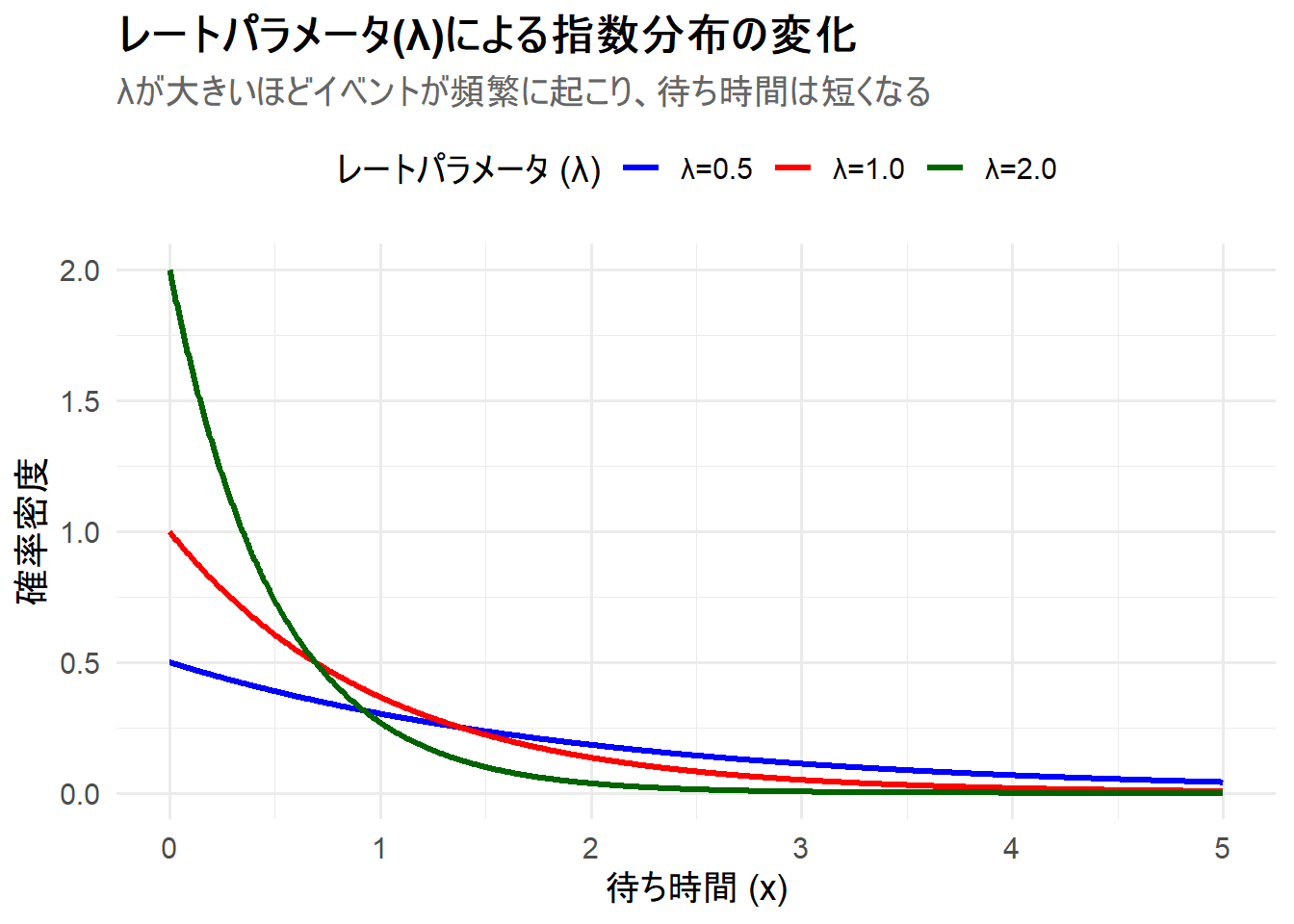
ここでは、レートパラメータ \(\lambda\) を変更した3つの指数分布を、1枚のチャートにggplot2を用いて描画します。これにより、レートパラメータが分布の形状に与える影響を視覚的に理解します。

ケース1: λ=0.5 （イベントが比較的稀に起こる。平均待ち時間は2）
ケース2: λ=1.0 （基準。平均待ち時間は1）
ケース3: λ=2.0 （イベントが頻繁に起こる。平均待ち時間は0.5）

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 5, length.out = 1000)

# 2. 異なるレートパラメータを持つ指数分布の確率密度を計算
# dexp(x, rate) を使用。rateがレートパラメータλ
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `λ=0.5` = dexp(x, rate = 0.5),
    `λ=1.0` = dexp(x, rate = 1.0),
    `λ=2.0` = dexp(x, rate = 2.0)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "λ=0.5",
    "λ=1.0",
    "λ=2.0"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  `λ=0.5` = "blue",
  `λ=1.0` = "red",
  `λ=2.0` = "darkgreen"
)

# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  geom_line(linewidth = 1.2) +
  scale_color_manual(values = manual_colors) +
  labs(
    title = "レートパラメータ(λ)による指数分布の変化",
    subtitle = "λが大きいほどイベントが頻繁に起こり、待ち時間は短くなる",
    x = "待ち時間 (x)",
    y = "確率密度",
    color = "レートパラメータ (λ)"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "top",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
print(p)

Figure 1 の解説

上記のRコードを実行すると、3つの指数分布が描画されたチャート Figure 1 が生成されます。

λ=0.5 (青線): レートが最も小さく、イベントが稀にしか起こらないケースです。分布の減少が最も緩やかで、長い待ち時間が発生する確率が他のケースより高くなっています。
λ=1.0 (赤線): 基準となるケースです。
λ=2.0 (緑線): レートが最も大きく、イベントが頻繁に起こるケースです。分布は\(x=0\)の近くで非常に高く、その後急速に減少しています。これは、待ち時間が非常に短い確率が高い（すぐに次のイベントが起こりやすい）ことを示しています。

このシミュレーションから、レートパラメータ \(\lambda\) が大きいほど、分布が左に圧縮され、より急峻な形状になることがわかります。これは、「イベント発生率が高いほど、平均待ち時間は短くなる」という直感的な理解に一致します。

以上です。