Rで確率分布:正規分布

確率密度関数 (Probability Density Function, PDF)

正規分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、以下の式で定義されます。

\[f(x | \mu, \sigma^2) = \dfrac{1}{\sqrt{2\pi\sigma^2}} e^{-\dfrac{(x-\mu)^2}{2\sigma^2}}\]

この関数は2つのパラメータによってその形状が決定されます。

• \(\mu\) (ミュー): 平均 (Mean)
  • 分布の中心の位置を決定します。グラフの対称軸が \(x=\mu\) となります。
  • 期待値 \(E[X] = \mu\) であり、確率変数がとる値の平均値です。
• \(\sigma^2\) (シグマ二乗): 分散 (Variance)
  • 分布の広がり具合（ばらつき）を決定します。
  • \(\sigma\)（シグマ）は標準偏差 (Standard Deviation) と呼ばれ、分散の正の平方根です。
  • \(\sigma\) が大きいほど、分布の山は低く、裾野は広く（データがばらついて）なります。
  • \(\sigma\) が小さいほど、分布の山は高く、裾野は狭く（データが平均値の周りに集中して）なります。
  • 分散 \(V[X] = E[(X-\mu)^2] = \sigma^2\) で表されます。

主な特徴

• 形状: 平均 \(\mu\) を中心に左右対称な釣鐘型（bell curve）をしています。
• 代表値: 平均値、中央値（Median）、最頻値（Mode）がすべて一致し、\(\mu\) となります。
• 68-95-99.7ルール: 確率変数 \(X\) が平均 \(μ\)、標準偏差 \(σ\) の正規分布に従う場合に平均値を中心とした幅に含まれるデータの割合が以下の3つの式に従うことを表しています。
  • \(P(\mu - \sigma \le X \le \mu + \sigma) \approx 0.6827\) (全体の約68%が平均±1標準偏差内に収まる)
  • \(P(\mu - 2\sigma \le X \le \mu + 2\sigma) \approx 0.9545\) (全体の約95%が平均±2標準偏差内に収まる)
  • \(P(\mu - 3\sigma \le X \le \mu + 3\sigma) \approx 0.9973\) (全体の約99.7%が平均±3標準偏差内に収まる)
• 標準正規分布 (Standard Normal Distribution): 特に、平均 \(\mu=0\)、分散 \(\sigma^2=1\)（つまり標準偏差 \(\sigma=1\)）の正規分布を標準正規分布と呼びます。その確率密度関数 \(\phi(z)\) は以下のように簡略化されます。 \[\phi(z) = \dfrac{1}{\sqrt{2\pi}} e^{-\dfrac{z^2}{2}}\] 任意の正規分布 \(X \sim N(\mu, \sigma^2)\) は、以下の標準化(Standardization)と呼ばれる変換により、標準正規分布 \(Z \sim N(0, 1)\) に変換できます。 \[Z = \dfrac{X - \mu}{\sigma}\]
• 中心極限定理 (Central Limit Theorem): 正規分布が極めて重要な理由の一つに、この定理があります。これは、「母集団がどのような分布であっても、そこから無作為抽出した標本の平均値の分布は、標本サイズ \(n\) が十分に大きいとき、正規分布に近似する」という定理です。この定理により、多くの自然現象や社会現象が正規分布でモデル化できる理論的根拠が与えられています。

Rコード

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(-10, 20, length.out = 1000)

# 2. 4つの異なるパラメータを持つ正規分布の確率密度を計算し、データフレームにまとめる
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `μ=0, σ=1 (標準)` = dnorm(x, mean = 0, sd = 1),
    `μ=0, σ=3` = dnorm(x, mean = 0, sd = 3),
    `μ=5, σ=1` = dnorm(x, mean = 5, sd = 1),
    `μ=10, σ=0.5` = dnorm(x, mean = 10, sd = 0.5)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 解説の順序と凡例の順序を合わせるために因子レベルを設定
  mutate(parameters = factor(parameters, levels = c(
    "μ=0, σ=1 (標準)",
    "μ=0, σ=3",
    "μ=5, σ=1",
    "μ=10, σ=0.5"
  )))

# 4. 各パラメータに割り当てる色を名前付きベクトルで定義
# ベクトルの名前が df_long$parameters の値と一致するようにする
manual_colors <- c(
  "μ=0, σ=1 (標準)" = "blue",
  "μ=0, σ=3" = "red",
  "μ=5, σ=1" = "darkgreen",
  "μ=10, σ=0.5" = "purple"
)


# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  geom_line(linewidth = 1.2) +
  # 色をマニュアルで指定するレイヤーを追加
  scale_color_manual(values = manual_colors) +
  labs(
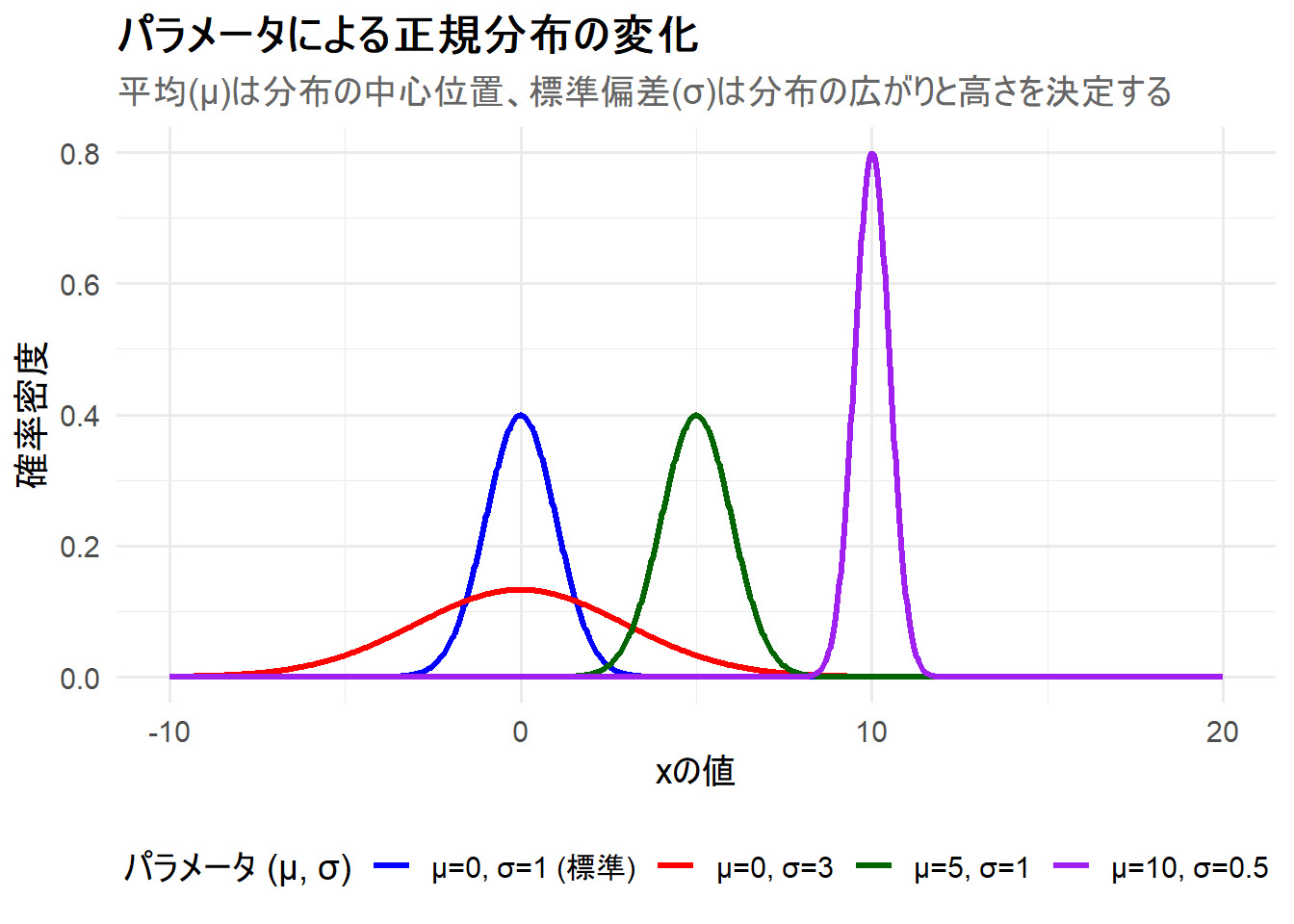
    title = "パラメータによる正規分布の変化",
    subtitle = "平均(μ)は分布の中心位置、標準偏差(σ)は分布の広がりと高さを決定する",
    x = "xの値",
    y = "確率密度",
    color = "パラメータ (μ, σ)"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "bottom",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
print(p)

Figure 1 の解説

上記のRコードを実行すると、4つの正規分布が描画されたチャート Figure 1 が生成されます。

• μ=0, σ=1 (青線): 基本となる標準正規分布です。中心が0にあり、標準的な広がりを持っています。
• μ=0, σ=3 (赤線): 標準正規分布（青線）と比較して、平均は同じ0ですが、標準偏差が3と大きくなっています。そのため、山の高さは低くなり、裾野が広く平たい分布になっていることがわかります。
• μ=5, σ=1 (緑線): 標準正規分布（青線）と比較して、標準偏差（広がり）は同じですが、平均が5に移動しています。これにより、グラフ全体が右に5だけ平行移動した形になります。
• μ=10, σ=0.5 (紫線): 平均が10に移動し、さらに標準偏差が0.5と非常に小さくなっています。そのため、データが平均10の周りに非常に集中し、鋭く尖った高い山の分布になっていることが確認できます。

以上です。