Rで確率分布:非心カイ2乗分布

非心カイ2乗分布の定義

独立な確率変数 \(Z_1, Z_2, \dots, Z_k\) が、それぞれ平均が0とは限らない正規分布 \(N(\mu_i, 1)\) に従うとします。

このとき、これらの確率変数を2乗して足し合わせた和

\[X = \displaystyle\sum_{i=1}^{k} Z_i^2\]

が従う分布を非心カイ2乗分布と呼びます。

この分布の形状は、2つのパラメータによって決定されます。一つは確率変数の個数である自由度 \(k\) です。そしてもう一つが、元の正規分布の平均のズレの大きさを示す非心性パラメータ \(\lambda\) です。

非心性パラメータ \(\lambda\) は、\(X\) を構成している各確率変数 \(Z_i\) の平均 \(\mu_i\) を用いて、以下のように定義されます。

\[\lambda = \displaystyle\sum_{i=1}^{k} \mu_i^2\]

つまり、確率変数 \(X\) の分布は、それを構成する \(Z_i\) の平均 \(\mu_i\) を通じて間接的に \(\lambda\) の影響を受けます。

この関係性を明確にするため、この分布を \(\chi^2(k, \lambda)\) と表記することがあります。

確率密度関数 (Probability Density Function, PDF)

自由度 \(k\)、非心性パラメータ \(\lambda\) の非心カイ2乗分布の確率密度関数 \(f(x)\) は、中心カイ2乗分布の確率密度にポアソン分布の重みをつけた無限級数で表されます。

\[f(x|k, \lambda) = \displaystyle\sum_{j=0}^{\infty} \left\{ \dfrac{e^{-\lambda/2} (\lambda/2)^j}{j!} \right\} f_{\chi^2(k+2j)}(x)\]

ここで \(f_{\chi^2(k+2j)}(x)\) は自由度 \(k+2j\) の中心カイ2乗分布のPDF

この分布は、以下の2つのパラメータによって形状が決定されます。

• \(k\): 自由度 (degrees of freedom, df)
  • 中心カイ2乗分布と同様に、2乗和を構成する独立な正規分布の個数です。
• \(\lambda\) (ラムダ): 非心性パラメータ (non-centrality parameter, ncp)
  • 元の正規分布の平均の2乗和 (\(\sum \mu_i^2\)) であり、分布の中心からの「ズレ」の大きさを表します。\(\lambda=0\) のとき、分布は中心カイ2乗分布と一致します。

主な特徴

• 定義域: 2乗和から成るため、確率変数は常に非負の値 (\(x \ge 0\)) をとります。
• 形状:
  • 非心性パラメータ \(\lambda\) が0のとき、中心カイ2乗分布と一致します。
  • \(\lambda\) が大きくなるにつれて、分布全体が右にシフトし、ばらつきが大きくなります。また、形状はより左右対称に近づきます。
• 代表値:
  • 平均 (Mean): \(k + \lambda\)
  • 分散 (Variance): \(2(k + 2\lambda)\)

  平均・分散ともに、中心カイ2乗分布 (\(k\) と \(2k\)) に非心性パラメータ \(\lambda\) の項が加わっていることがわかります。

Rコード

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 45, length.out = 1000)

# 2. 異なるパラメータを持つ非心カイ2乗分布の確率密度を計算
# dchisq(x, df, ncp) を使用。ncpが非心性パラメータλ
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `k=5, λ=0`  = dchisq(x, df = 5, ncp = 0),
    `k=5, λ=5`  = dchisq(x, df = 5, ncp = 5),
    `k=5, λ=10` = dchisq(x, df = 5, ncp = 10),
    `k=10, λ=5` = dchisq(x, df = 10, ncp = 5)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "k=5, λ=0",
    "k=5, λ=5",
    "k=5, λ=10",
    "k=10, λ=5"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  "k=5, λ=0"  = "black",
  "k=5, λ=5"  = "blue",
  "k=5, λ=10" = "red",
  "k=10, λ=5" = "darkgreen"
)

# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  geom_line(linewidth = 1.2) +
  scale_color_manual(values = manual_colors) +
  labs(
    title = "非心カイ2乗分布の変化",
    subtitle = "非心性パラメータ(λ)は分布を右にシフトさせ、ばらつきを大きくする",
    x = "xの値",
    y = "確率密度",
    color = "パラメータ (k, λ)"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "top",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
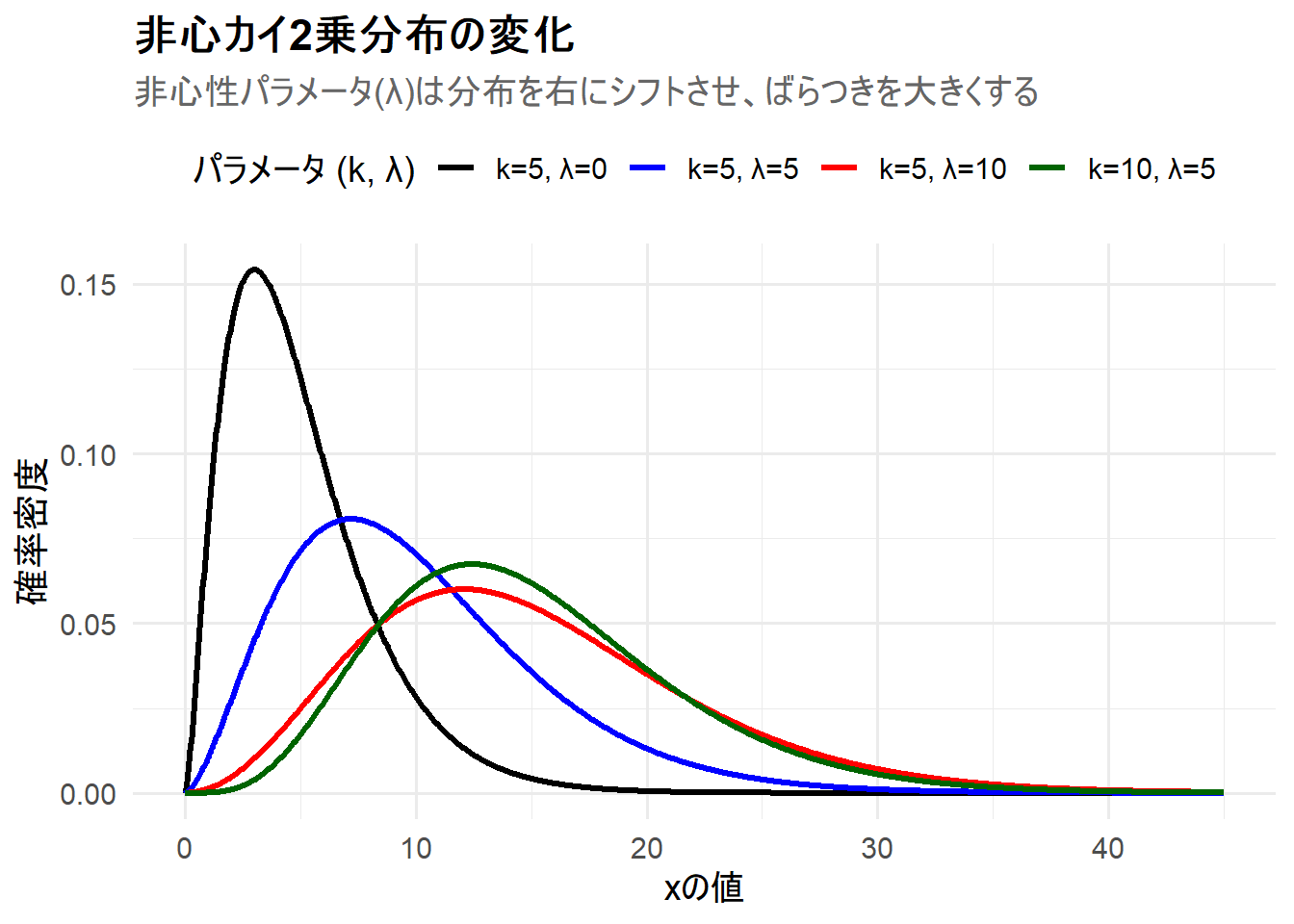
print(p)

Figure 1 の解説

上記のRコードを実行すると、4つの非心カイ2乗分布が描画されたチャート Figure 1 が生成されます。

• k=5, λ=0 (黒線): 比較の基準となる中心カイ2乗分布です。右に歪んだ形状をしています。
• k=5, λ=5 (青線): 黒線と同じ自由度ですが、非心性パラメータ \(\lambda=5\) が加わっています。分布全体が右にシフトし、ばらつきが大きくなっている（山の高さが低く、裾が広くなっている）ことがわかります。
• k=5, λ=10 (赤線): 非心性パラメータがさらに大きい \(\lambda=10\) になったケースです。青線よりもさらに右にシフトし、より左右対称に近い形状になっているのが確認できます。
• k=10, λ=5 (緑線): この分布の平均は \(k+\lambda=15\) となり、赤線（平均15）と同一ですが、分散は \(2(10+2\times 5)=40\) となり、赤線の分散 \(2(5+2\times 10)=50\) よりも小さくなります。そのため、赤線よりも分布がやや平均の周りに集中した（ばらつきが小さい）形状になっています。

このシミュレーションから、非心性パラメータ \(\lambda\) が、分布の中心（平均）と広がり（分散）の両方に影響を与え、その値が大きくなるほど分布が右へ移動していく様子が明確に理解できます。これは、対立仮説における「効果（ズレ）」が大きくなるほど、検定統計量がより大きな値を取りやすくなるという直感に対応します。

以上です。