Rで 確率分布:非心F分布 を試みます。
本ポストはこちらの続きです。

本ポストでは「非心F分布」と区別するために「F分布」を「中心F分布(central F distribution)」と呼び、「非心カイ2乗分布」と区別するために「カイ2乗分布」を「中心カイ2乗分布」と呼びます。
1. 非心F分布とは
非心F分布(Non-central F-distribution)は、中心F分布を一般化したものです。中心F分布が「2つの中心カイ2乗分布の比」から作られるのに対し、非心F分布は「分子が非心カイ2乗分布、分母が中心カイ2乗分布の比」から構成されます。
この分布は、分散分析(ANOVA)や回帰分析におけるF検定で、対立仮説(効果がある、差がある)が真であるときの検定統計量の分布を記述するために不可欠です。
非心F分布の定義
独立な確率変数 \(U_1\) と \(U_2\) が、それぞれ
- \(U_1 \sim \chi^2(d_1, \lambda)\) (自由度 \(d_1\)、非心性パラメータ \(\lambda\) の非心カイ2乗分布)
- \(U_2 \sim \chi^2(d_2)\) (自由度 \(d_2\) の中心カイ2乗分布)
に従うとします。このとき、それぞれのカイ2乗変数をその自由度で割ったものの比、
\[F = \dfrac{U_1/d_1}{U_2/d_2}\]
が従う分布が、分子の自由度 \(d_1\)、分母の自由度 \(d_2\)、非心性パラメータ \(\lambda\) の非心F分布です。
確率密度関数 (Probability Density Function, PDF)
非心F分布の確率密度関数の分布は、3つのパラメータによってその形状が決定されます。
- \(d_1\): 分子の自由度 (numerator degrees of freedom)
- \(d_2\): 分母の自由度 (denominator degrees of freedom)
- \(\lambda\) (ラムダ): 非心性パラメータ (non-centrality parameter, ncp)
- 分子の非心カイ2乗分布から引き継がれるパラメータで、分布の中心からの「ズレ」の大きさを表します。
- \(\lambda=0\) のとき、分子は中心カイ2乗分布となり、分布全体は中心F分布と完全に一致します。
主な特徴
- 定義域: 分散の比であるため、確率変数は常に非負の値 (\(x \ge 0\)) をとります。
- 形状:
- \(\lambda=0\) のときは、中心F分布(右に歪んだ山型)。
- \(\lambda > 0\) のときは、中心F分布と比較して分布全体が右にシフトし、ばらつきが大きくなります(山が低く、裾が広くなる)。
- 代表値:
- 平均 (Mean): \(E[F] = \dfrac{d_2\left(d_1+\lambda\right)}{d_1\left(d_2-2\right)}\) (ただし、\(d_2 > 2\))
- 分散も平均と同様に3つのパラメータすべてに依存します。
- 他の分布との関係:
- 確率変数 \(T\) が自由度 \(k\)、非心性パラメータ \(\delta\) の非心t分布に従うとき、その2乗 \(T^2\) は、自由度(1, k)、非心性パラメータ \(\lambda=\delta^2\) の非心F分布に従います。\(T^2 \sim F(1, k, \delta^2)\)。
2. 非心F分布の応用例
非心F分布の最も重要な応用は、分散分析(ANOVA)や回帰分析における検出力(Power)の計算です。
- 分散分析(ANOVA)における検出力の計算
- 3つ以上のグループの母平均に差があるかを検定するANOVAを考えます。
- 帰無仮説 \(H_0\)(全ての群平均は等しい)が真のとき: 検定統計量Fは、中心F分布に従います。この分布を使って、棄却域(例えば上位5%点)を決定します。
- 対立仮説 \(H_1\)(少なくとも一つの群平均は異なる)が真のとき: 検定統計量Fは、非心F分布に従います。非心性パラメータ \(\lambda\) の値は、群平均が実際にどれだけ異なっているか(効果量)によって決まります。
- この対立仮説下での分布(非心F分布)が、帰無仮説で定められた棄却域に入る確率を計算することで、その検定の検出力を求めることができます。
- 3つ以上のグループの母平均に差があるかを検定するANOVAを考えます。
3. R言語によるシミュレーション
ここでは、自由度 \((d_1, d_2)\) と非心性パラメータ \(\lambda\) を変更した4つの非心F分布を1枚のチャートに描画します。これにより、非心性パラメータが分布の形状に与える影響を視覚的に理解します。
- ケース1:
d1=4, d2=30, λ=0(中心F分布。比較の基準) - ケース2:
d1=4, d2=30, λ=5(自由度は同じで、非心性を加える) - ケース3:
d1=4, d2=30, λ=15(非心性をさらに大きくする) - ケース4:
d1=4, d2=10, λ=5(分母の自由度を小さくする)
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 10, length.out = 1000)
# 2. 異なるパラメータを持つ非心F分布の確率密度を計算
# df(x, df1, df2, ncp) を使用。ncpが非心性パラメータλ
df <- tibble(
x = x_vals
) %>%
mutate(
`d1=4, d2=30, λ=0` = df(x, df1 = 4, df2 = 30, ncp = 0),
`d1=4, d2=30, λ=5` = df(x, df1 = 4, df2 = 30, ncp = 5),
`d1=4, d2=30, λ=15` = df(x, df1 = 4, df2 = 30, ncp = 15),
`d1=4, d2=10, λ=5` = df(x, df1 = 4, df2 = 10, ncp = 5)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"d1=4, d2=30, λ=0",
"d1=4, d2=30, λ=5",
"d1=4, d2=30, λ=15",
"d1=4, d2=10, λ=5"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`d1=4, d2=30, λ=0` = "black",
`d1=4, d2=30, λ=5` = "blue",
`d1=4, d2=30, λ=15` = "red",
`d1=4, d2=10, λ=5` = "darkgreen"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
labs(
title = "非心F分布の変化",
subtitle = "非心性パラメータ(λ)は分布を右にシフトさせ、ばらつきを大きくする",
x = "F値",
y = "確率密度",
color = "パラメータ (d1, d2, λ)"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
print(p)Figure 1 の解説
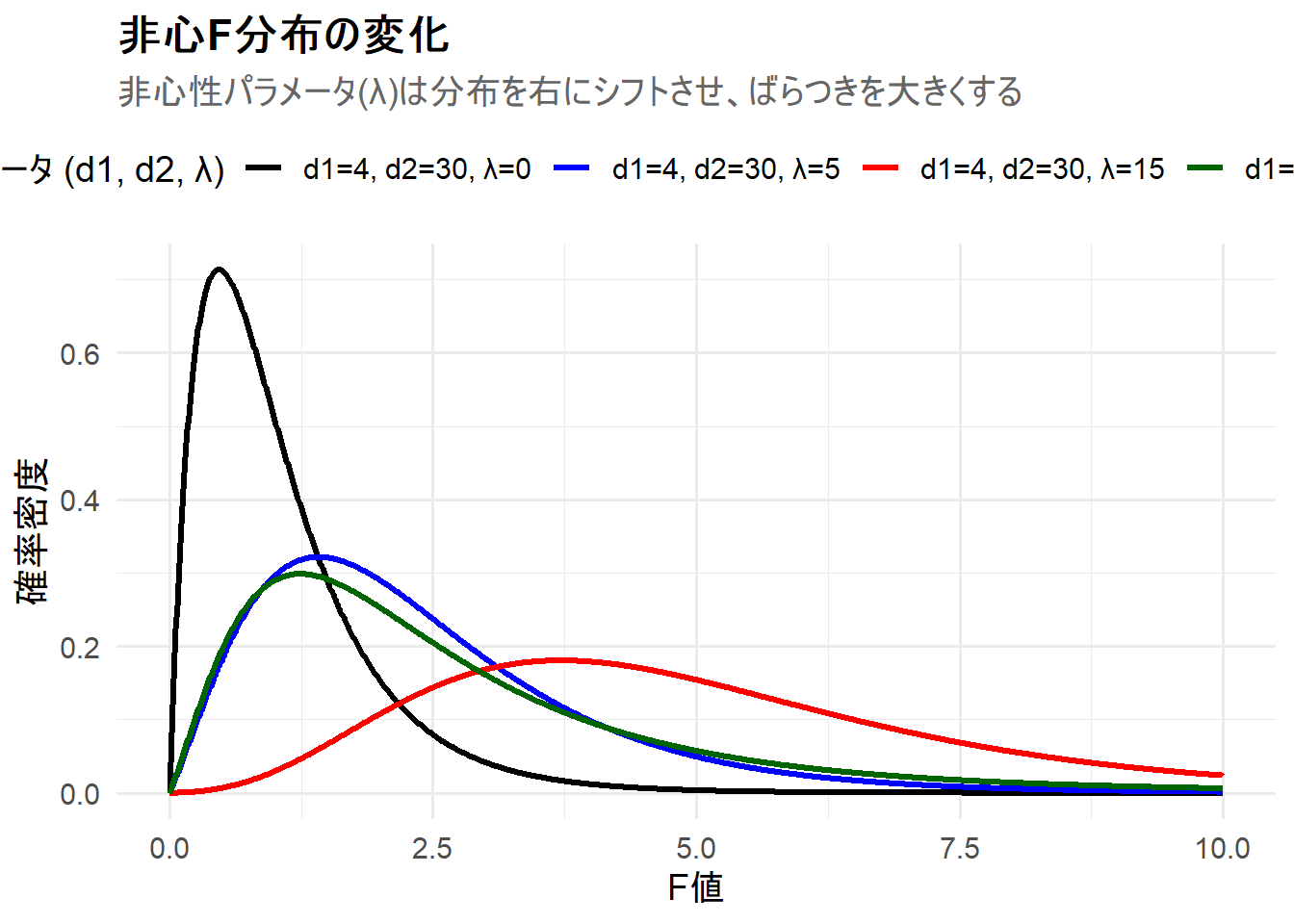
上記のRコードを実行すると、4つの非心F分布が描画されたチャート Figure 1 が生成されます。
-
d1=4, d2=30, λ=0(黒線): 比較の基準となる中心F分布です。ピークが1の近くにあり、右に歪んだ形状をしています。これは帰無仮説(真の差がない)のもとでのF統計量の分布です。 -
d1=4, d2=30, λ=5(青線): 黒線と同じ自由度ですが、非心性パラメータ \(\lambda=5\) が加わっています。分布全体が右にシフトし、山が低く平たくなっている(ばらつきが大きくなっている)ことがわかります。 -
d1=4, d2=30, λ=15(赤線): 非心性パラメータがさらに大きい \(\lambda=15\) になったケースです。青線よりもさらに大きく右にシフトし、より平坦な分布になっています。 -
d1=4, d2=10, λ=5(緑線): 青線と同じ非心性パラメータですが、分母の自由度 \(d_2\) が30から10に小さくなっています。これにより分布のばらつきがさらに大きくなり、青線よりもさらに低く、平坦な形状になっていることが確認できます。
このシミュレーションから、非心性パラメータ \(\lambda\) が大きいほど(=対立仮説における効果量が大きいほど)、F統計量の分布が右にシフトしていく様子がわかります。ANOVAで棄却域を設定した場合、\(\lambda\) が大きいほど分布の右側の裾が棄却域に大きくかかることになり、検出力が高まるというメカニズムを視覚的に理解することができます。
対立仮説における効果量が大きいほどとは
ある研究者が、3種類の新しい肥料(A, B, C)がトウモロコシの収穫量に与える影響を調べたいと考えています。
- 帰無仮説 (\(H_0\)): 「3種類の肥料の間に効果の差はない」
- つまり、どの肥料を使っても、トウモロコシの平均収穫量は同じである。(\(\mu_A = \mu_B = \mu_C\))
- 対立仮説 (\(H_1\)): 「少なくとも1種類の肥料は、他の肥料と効果が異なる」
- 3つの平均収穫量のうち、少なくとも1つは他と異なる。
ここで、「効果量」とは、この対立仮説が「どのくらい本当か」の度合い、つまりグループ間の真の平均値が、実際にどれだけ異なっているかの大きさを指します。
以下に、「効果量が小さい」対立仮説と「効果量が大きい」対立仮説の具体的な例を示します。
例1:効果量が「小さい」対立仮説
- 肥料Aの真の平均収穫量: 50.5 kg
- 肥料Bの真の平均収穫量: 50.0 kg
- 肥料Cの真の平均収穫量: 49.5 kg
この場合、対立仮説(差がある)は真実ですが、その差は非常にわずかです。 実際にデータを集めても、このわずかな差は、天候や土壌の個体差といった「偶然のばらつき(誤差)」に埋もれてしまいがちです。
例2:効果量が「大きい」対立仮説
- 肥料Aの真の平均収穫量: 60 kg
- 肥料Bの真の平均収穫量: 50 kg
- 肥料Cの真の平均収穫量: 40 kg
この場合も対立仮説は真実ですが、今度はその差が非常に大きいです。 これだけハッキリとした差があれば、偶然のばらつきがあったとしても、データからその差を検出するのは比較的容易でしょう。
まとめ
| 効果量が小さい対立仮説 | 効果量が大きい対立仮説 | |
|---|---|---|
| 具体的な状況 | グループ間の「真の差」がわずか | グループ間の「真の差」が明確 |
| 非心性パラメータ \(\lambda\) | 小さい | 大きい |
| 検出力 | 低い(差を見逃しやすい) | 高い(差を検出しやすい) |
したがって、「対立仮説における効果量が大きいほど」とは、「比較したいグループ間の、『本当の差』が大きいほど」 という意味になります。そして、その「本当の差」が大きいほど、統計検定は、その差を正しく「有意差あり」と判定できる能力(=検出力)が高まる、ということです。
4. 検出力のシミュレーション
検出力は、「対立仮説が真であるとき、検定統計量が棄却域に入る確率」です。これは、非心F分布の確率密度関数を、棄却域の範囲で積分することで求められます。
1. シナリオ設定
分散分析(ANOVA)を想定した、具体的なシナリオを設定します。
- 検定の種類: 一元配置分散分析 (One-way ANOVA)
- グループ数: 5群
- 各グループのサンプルサイズ: 7人
- この設定により、分子の自由度 \(d_1 = 5 - 1 = 4\)
- 分母の自由度 \(d_2 = 5 \times (7-1) = 30\)
- これは Figure 1 のシミュレーションのパラメータ(黒、青、赤の線)と一致します。
- 有意水準 \(\alpha\): 0.05
- 非心性パラメータ \(\lambda\): 0, 5, 15 の3つのケースを比較
2. 関数 df() と integrate() を利用した検出力の計算
Step 1: 棄却域の決定
まず、帰無仮説(中心F分布, λ=0)のもとで、F統計量が上位5%に入る境界値(臨界値)を求めます。
# 各パラメータを設定
d1 <- 4
d2 <- 30
alpha <- 0.05
# 臨界値を計算 (P(F > critical_value) = alpha となる値)
critical_value <- qf(1 - alpha, df1 = d1, df2 = d2)
cat(paste("臨界値:", round(critical_value, 4)))臨界値: 2.6896棄却域は F > 2.6896 となります。
Step 2: 確率密度関数を積分して検出力を計算
次に、各非心性パラメータ \(\lambda\) のもとでの非心F分布 (df(x, df1, df2, ncp)) を、この棄却域(2.6896 から無限大まで)で積分します。
# ケース1: λ = 0 の場合 (これは第1種の過誤の確率αと一致する)
power_lambda0 <- integrate(
function(x) df(x, df1 = d1, df2 = d2, ncp = 0),
lower = critical_value,
upper = Inf
)$value
# ケース2: λ = 5 の場合
power_lambda5 <- integrate(
function(x) df(x, df1 = d1, df2 = d2, ncp = 5),
lower = critical_value,
upper = Inf
)$value
# ケース3: λ = 15 の場合
power_lambda15 <- integrate(
function(x) df(x, df1 = d1, df2 = d2, ncp = 15),
lower = critical_value,
upper = Inf
)$value
# 結果をデータフレームにまとめる
results_df <- data.frame(
lambda = c(0, 5, 15),
power_by_df = c(power_lambda0, power_lambda5, power_lambda15)
)
cat("--- 非心性パラメータ毎の検出力 ---\n\n")
print(results_df)--- 非心性パラメータ毎の検出力 ---
lambda power_by_df
1 0 0.04999998
2 5 0.34208849
3 15 0.83103854この結果から、非心性パラメータ \(\lambda\) が0から5、15と大きくなるにつれて、検出力が 5% → 34.2% → 83.1% と上昇していることが数値で明確に確認できました。
2. パッケージ pwr を利用した結果との比較
次に、パッケージ pwr の結果と比較します。
注意点: pwr.anova.test() 関数では、非心性パラメータ \(\lambda\) の代わりに、効果量 (Cohen’s f) を用います。両者の間には以下の関係があります(\(k\): グループ数, \(n\): 1グループのサンプルサイズ)。
\[\lambda = n \cdot k \cdot f^2\]
この関係を使い、\(\lambda\) を \(f\) に変換してから関数に入力します。\[f = \sqrt{\dfrac{\lambda}{n \cdot k}}\]
library(pwr)
# グループ数と1グループのサンプルサイズ
groups_k <- d1 + 1
n_per_group <- (d2 / groups_k) + 1
# ケース1: λ = 0 (効果量f=0)
f_val0 <- sqrt(0 / (n_per_group * groups_k))
pwr_result0 <- pwr.anova.test(
k = groups_k, n = n_per_group, f = f_val0,
sig.level = alpha
)$power
# ケース2: λ = 5
f_val5 <- sqrt(5 / (n_per_group * groups_k))
pwr_result5 <- pwr.anova.test(
k = groups_k, n = n_per_group, f = f_val5,
sig.level = alpha
)$power
# ケース3: λ = 15
f_val15 <- sqrt(15 / (n_per_group * groups_k))
pwr_result15 <- pwr.anova.test(
k = groups_k, n = n_per_group, f = f_val15,
sig.level = alpha
)$power
# 比較結果を元のデータフレームに追加
results_df$power_by_pwr <- c(pwr_result0, pwr_result5, pwr_result15)
cat("--- 関数 pwr.anova.test との比較 ---\n\n")
print(results_df)--- 関数 pwr.anova.test との比較 ---
lambda power_by_df power_by_pwr
1 0 0.04999998 0.0500000
2 5 0.34208849 0.3420885
3 15 0.83103854 0.8310385df関数を積分して求めた検出力 (power_by_df) と、pwrパッケージを用いて計算した検出力 (power_by_pwr) の結果は一致しました。
以上です。