Rで 確率分布:非心t分布 を試みます。
本ポストはこちらの続きです。

本ポストでは「非心t分布」と区別するために「t分布」を「中心t分布(central t distribution)」と呼びます。
1. 非心t分布とは
非心t分布(Non-central t-distribution)は、スチューデントのt分布(中心t分布)を一般化したものです。中心t分布が「帰無仮説(効果がない、差がない)」のもとでの統計量の分布を記述するのに対し、非心t分布は「対立仮説(効果がある、差がある)」のもとでの分布を記述するために用いられます。
非心t分布の定義
非心t分布の成り立ちは、中心t分布の定義に「ズレ」の項を加えることで理解できます。 独立な確率変数 \(Z\) と \(U\) が、それぞれ
- \(Z \sim N(0, 1)\) (標準正規分布)
- \(U \sim \chi^2(k)\) (自由度 \(k\) のカイ2乗分布)
に従うとします。このとき、以下の式で定義される確率変数 \(T\)
\[T = \dfrac{Z+\delta}{\sqrt{U/k}}\]
が従う分布が、自由度 \(k\)、非心性パラメータ \(\delta\) の非心t分布です。
- 中心t分布の定義式 \(T = \dfrac{Z}{\sqrt{U/k}}\) と比較すると、分子の標準正規分布 \(Z\) に、定数である非心性パラメータ \(\delta\) が加えられている点が唯一の違いです。この \(\delta\) が、分布の中心からの「ズレ」を表します。
確率密度関数 (Probability Density Function, PDF)
非心t分布の確率密度関数の分布の形状は以下の2つのパラメータで決定されます。
- \(k\): 自由度 (degrees of freedom, df)
- 中心t分布と同様に、分布の裾の重さを決定します。標本サイズに関連します(通常は \(k=n-1\))。
- \(\delta\) (デルタ): 非心性パラメータ (non-centrality parameter, ncp)
- 分布の非対称性を決定するパラメータです。
- \(\delta=0\) のとき、分布は中心t分布と完全に一致し、左右対称になります。
- \(\delta \neq 0\) のとき、分布は左右非対称になります。\(\delta\) の値が分布の中心をシフトさせるような効果を持ちます。
主な特徴
- 形状:
- \(\delta=0\) のときは、平均0を中心とする左右対称な釣鐘型(中心t分布)。
- \(\delta > 0\) のときは、分布の山が右にシフトし、左の裾が重くなるような非対称な形状になります。
- \(\delta < 0\) のときは、分布の山が左にシフトします。
- 他の分布との関係: \(\delta=0\) のとき、中心t分布に一致します。また、自由度 \(k\) が大きくなると、平均 \(\delta\)、分散 1 の正規分布に近づきます。
- 代表値:
- 平均 (Mean): \(\delta \sqrt{\dfrac{k}{2}} \dfrac{\Gamma((k-1)/2)}{\Gamma(k/2)}\) (ただし、\(k>1\))。近似的には \(\delta\) に近い値をとります。
- 分散も平均と同様に \(\delta\) と \(k\) の両方に依存します。
2. 非心t分布の応用例
非心t分布の最も重要な応用は、t検定における検出力(Power)の計算です。
- t検定の検出力の計算
- 検出力とは、「対立仮説が真であるときに、それを正しく採択(帰無仮説を棄却)する確率」です。
- 1標本t検定を例に考えます。帰無仮説 \(H_0: \mu = \mu_0\) に対し、対立仮説が \(H_1: \mu = \mu_1 (\neq \mu_0)\) であるとします。
- 帰無仮説 \(H_0\) が真のとき: 検定統計量 \(t = \dfrac{\bar{X}-\mu_0}{s/\sqrt{n}}\) は、中心t分布に従います。
- 対立仮説 \(H_1\) が真のとき: 検定統計量 \(t\) は、非心t分布に従います。このときの非心性パラメータは、効果の大きさ(効果量)を標準化した \(\delta = \dfrac{\mu_1-\mu_0}{\sigma/\sqrt{n}}\) となります。
- この対立仮説下での分布(非心t分布)を考えることで、「真の平均が \(\mu_1\) のときに、検定結果が有意になる(t値が棄却域に入る)確率」を計算できます。これが検出力です。
- 実験に必要なサンプルサイズを設計する際、「これくらいの効果があるなら、80%の確率でそれを検出できるようにしたい」といった目標を設定し、それを満たす \(n\) を非心t分布を用いて逆算します。
3. R言語によるシミュレーション
ここでは、自由度 \(k\) を固定し、非心性パラメータ \(\delta\) を変更した4つの非心t分布を1枚のチャートに描画します。これにより、非心性パラメータが分布の形状に与える影響を視覚的に理解します。
- ケース1:
k=10, δ=0(中心t分布。左右対称) - ケース2:
k=10, δ=2(正の非心性パラメータ。右にシフト) - ケース3:
k=10, δ=5(より大きな正の非心性パラメータ) - ケース4:
k=10, δ=-2(負の非心性パラメータ。左にシフト)
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(-8, 12, length.out = 1000)
# 2. 異なるパラメータを持つ非心t分布の確率密度を計算
# dt(x, df, ncp) を使用。ncpが非心性パラメータδ
df <- tibble(
x = x_vals
) %>%
mutate(
`k=10, δ=0` = dt(x, df = 10, ncp = 0),
`k=10, δ=2` = dt(x, df = 10, ncp = 2),
`k=10, δ=5` = dt(x, df = 10, ncp = 5),
`k=10, δ=-2` = dt(x, df = 10, ncp = -2)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"k=10, δ=0",
"k=10, δ=2",
"k=10, δ=5",
"k=10, δ=-2"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
"k=10, δ=0" = "black",
"k=10, δ=2" = "blue",
"k=10, δ=5" = "red",
"k=10, δ=-2" = "darkgreen"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
labs(
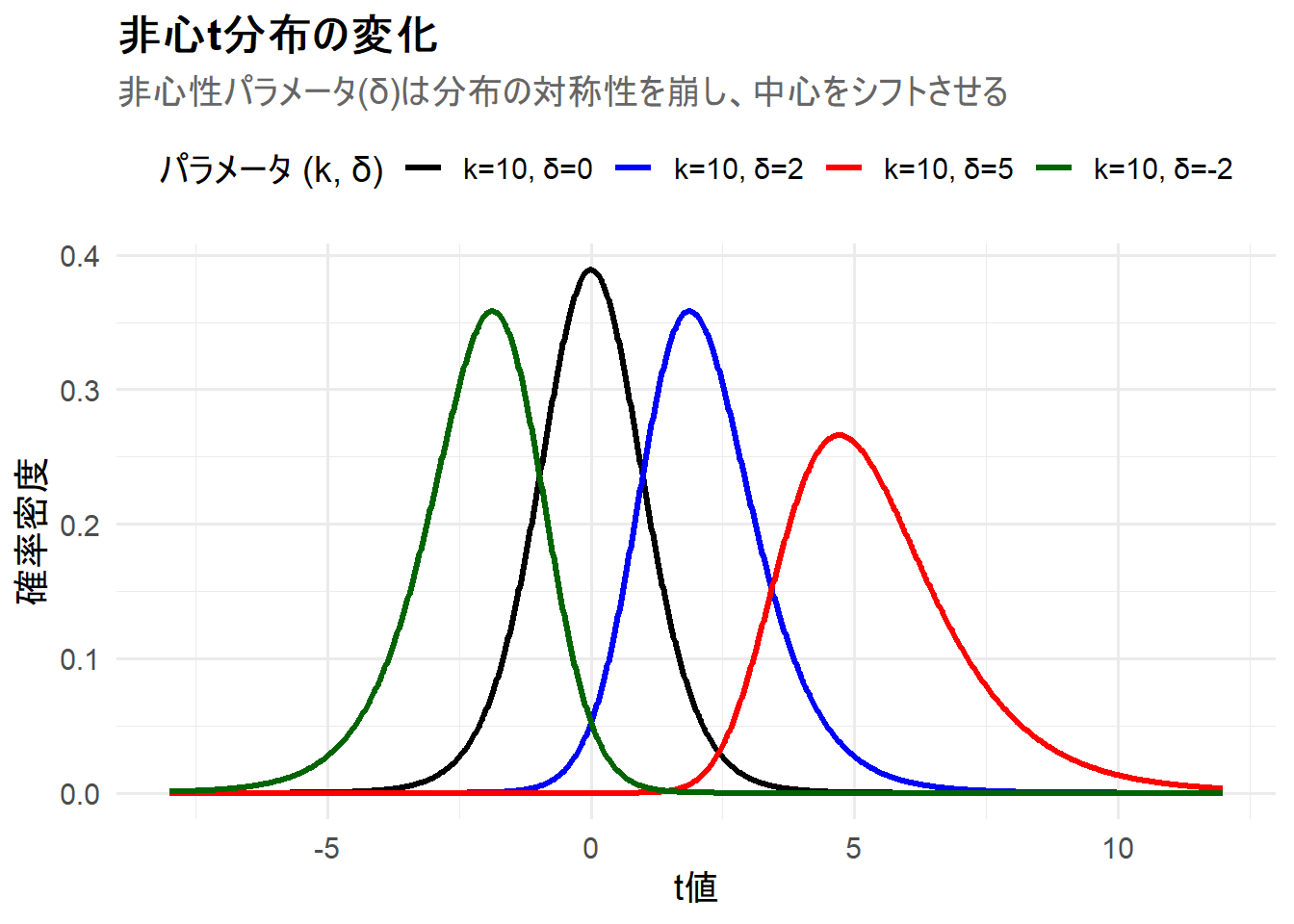
title = "非心t分布の変化",
subtitle = "非心性パラメータ(δ)は分布の対称性を崩し、中心をシフトさせる",
x = "t値",
y = "確率密度",
color = "パラメータ (k, δ)"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、4つの非心t分布が描画されたチャート Figure 1 が生成されます。
-
k=10, δ=0(黒線): 比較の基準となる中心t分布です。0を中心とした左右対称な釣鐘型をしています。これは帰無仮説(真の差がない)のもとでのt統計量の分布です。 -
k=10, δ=2(青線): 非心性パラメータが正の値(\(\delta=2\))のため、分布全体が右にシフトし、形状が左右非対称になっていることがわかります。 -
k=10, δ=5(赤線): 非心性パラメータがさらに大きい(\(\delta=5\))ケースです。青線よりもさらに大きく右にシフトしています。これは、対立仮説における「真の効果量」が大きいほど、観測されるt値も大きくなる傾向があることを示しています。 -
k=10, δ=-2(緑線): 非心性パラメータが負の値(\(\delta=-2\))のため、分布全体が左にシフトしています。
このシミュレーションから、非心性パラメータ \(\delta\) が、t統計量の分布の中心を「真の効果量」の方向にシフトさせる役割を持つことが直感的に理解できます。t検定で棄却域(例えばt > 2など)を設定した場合、\(\delta\) が大きいほど分布全体が棄却域にかかる面積が大きくなり、結果として「検出力が高まる」というメカニズムが視覚的にわかります。
4. 検出力のシミュレーション
検出力は、「対立仮説が真であるとき、検定統計量が棄却域に入る確率」でした。これは、非心t分布の確率密度関数を、棄却域の範囲で積分することで求められます。
1. シナリオ設定
- 検定の種類: 1標本t検定(片側)
- 自由度 \(k\): 10 (標本サイズ \(n=11\))
- 有意水準 \(\alpha\): 0.05
- 非心性パラメータ \(\delta\)(真の効果量): 0, 2, 5 の3つのケースを比較
2. 関数 dt() と integrate() を利用した検出力の計算
Step 1: 棄却域の決定
まず、帰無仮説(中心t分布, δ=0)のもとで、t統計量が上位5%に入る境界値(臨界値)を求めます。
# 自由度と有意水準
k <- 10
alpha <- 0.05
# 臨界値を計算 (P(T > critical_value) = alpha となる値)
critical_value <- qt(1 - alpha, df = k)
cat(paste("臨界値:", round(critical_value, 4)))臨界値: 1.8125棄却域は t > 1.8125 となります。
Step 2: 確率密度関数を積分して検出力を計算
次に、各非心性パラメータ \(\delta\) のもとでの非心t分布 (dt(x, df, ncp)) を、この棄却域(1.8125 から無限大まで)で積分します。Rのintegrate()関数を使います。
# ケース1: δ = 0 の場合 (第1種の過誤の確率αと一致する)
power_delta0 <- integrate(
function(x) dt(x, df = k, ncp = 0),
lower = critical_value,
upper = Inf
)$value
# ケース2: δ = 2 の場合
power_delta2 <- integrate(
function(x) dt(x, df = k, ncp = 2),
lower = critical_value,
upper = Inf
)$value
# ケース3: δ = 5 の場合
power_delta5 <- integrate(
function(x) dt(x, df = k, ncp = 5),
lower = critical_value,
upper = Inf
)$value
# 結果をデータフレームにまとめる
results_df <- data.frame(
delta = c(0, 2, 5),
power_by_dt = c(power_delta0, power_delta2, power_delta5)
)
cat("--- 非心性パラメータ毎の検出力 ---\n\n")
print(results_df)--- 非心性パラメータ毎の検出力 ---
delta power_by_dt
1 0 0.0500000
2 2 0.5861093
3 5 0.9985829この結果から、非心性パラメータ \(\delta\) が0から2、5と大きくなるにつれて、検出力が 5% → 58.6% → 99.9% と上昇していることが確認できました。\(\delta=0\) のときの検出力が、設定した有意水準 5% と一致していることもわかります。
2. パッケージ pwr を利用した結果との比較
次に、パッケージ pwr の結果と比較します。
注意点: pwrパッケージでは、非心性パラメータ \(\delta\) の代わりに、効果量 (Cohen’s d) を用います。両者の間には以下の関係があります。
\[d = \dfrac{\delta}{\sqrt{n}}\]
この関係を使って、\(\delta\) を \(d\) に変換してから pwr.t.test() 関数に入力します。
library(pwr)
# 標本サイズ
n <- k + 1
# ケース1: δ = 0 (効果量d=0)
d_val0 <- 0 / sqrt(n)
pwr_result0 <- pwr.t.test(
n = n, d = d_val0, sig.level = alpha,
type = "one.sample", alternative = "greater"
)$power
# ケース2: δ = 2 (効果量d=2/√11)
d_val2 <- 2 / sqrt(n)
pwr_result2 <- pwr.t.test(
n = n, d = d_val2, sig.level = alpha,
type = "one.sample", alternative = "greater"
)$power
# ケース3: δ = 5 (効果量d=5/√11)
d_val5 <- 5 / sqrt(n)
pwr_result5 <- pwr.t.test(
n = n, d = d_val5, sig.level = alpha,
type = "one.sample", alternative = "greater"
)$power
# 比較結果を元のデータフレームに追加
results_df$power_by_pwr <- c(pwr_result0, pwr_result2, pwr_result5)
cat("--- 関数 pwr.t.test との比較 ---\n\n")
print(results_df)--- 関数 pwr.t.test との比較 ---
delta power_by_dt power_by_pwr
1 0 0.0500000 0.0500000
2 2 0.5861093 0.5861093
3 5 0.9985829 0.9985829dt関数を積分して求めた検出力 (power_by_dt) と、pwrパッケージを用いて計算した検出力 (power_by_pwr) の結果は一致しました。
以上です。