Rで確率分布:F分布

F分布の定義

F分布の定義は、その応用を理解する上で非常に重要です。 独立な確率変数 \(U_1\) と \(U_2\) が、それぞれ

• \(U_1 \sim \chi^2(d_1)\) （自由度 \(d_1\) のカイ2乗分布）
• \(U_2 \sim \chi^2(d_2)\) （自由度 \(d_2\) のカイ2乗分布）

に従うとします。このとき、それぞれのカイ2乗変数をその自由度で割ったものの比、

\[F = \dfrac{U_1/d_1}{U_2/d_2}\]

が従う分布が、分子の自由度 \(d_1\)、分母の自由度 \(d_2\) のF分布です。 \(U_1/d_1\) と \(U_2/d_2\) は、平均平方（Mean Square）と呼ばれ、分散の推定量と見なせます。したがって、F分布は「2つの分散の推定量の比」がどのような分布をとるかを示していると解釈できます。

確率密度関数 (Probability Density Function, PDF)

自由度 \((d_1, d_2)\) のF分布に従う確率変数 \(F\) の確率密度関数 \(f(x)\) は、以下の式で定義されます。

\[f(x | d_1, d_2) = \dfrac{\sqrt{\dfrac{(d_1x)^{d_1}d_2^{d_2}}{(d_1x+d_2)^{d_1+d_2}}}}{x \cdot B\left(\dfrac{d_1}{2}, \dfrac{d_2}{2}\right)} \quad (x \ge 0)\] ここで \(B\) はベータ関数です。

この分布は、2つのパラメータによって形状が決定されます。

• \(d_1\): 分子の自由度 (numerator degrees of freedom)
  • 定義式の分子に来るカイ2乗分布の自由度です。
• \(d_2\): 分母の自由度 (denominator degrees of freedom)
  • 定義式の分母に来るカイ2乗分布の自由度です。

主な特徴

• 定義域: 分散の比であるため、確率変数は常に非負の値 (\(x \ge 0\)) をとります。
• 形状: カイ2乗分布と同様に、右に大きく歪んだ（裾を引く）非対称な形状をしています。その具体的な形状は、2つの自由度 \(d_1\) と \(d_2\) の組み合わせによって決まります。
• 自由度の影響:
  • 一般的に、両方の自由度が大きくなるにつれて、分布の歪みは小さくなり、ピークは1の周りに集中し、より尖った形状になります。
• 他の分布との関係:
  • 確率変数 \(T\) が自由度 \(k\) のt分布に従うとき、その2乗 \(T^2\) は、自由度(1, k)のF分布に従います。\(T^2 \sim F(1, k)\)。

Rコード

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 5, length.out = 1000)

# 2. 異なる自由度を持つF分布の確率密度を計算
# df(x, df1, df2) を使用。df1が分子、df2が分母の自由度
df <- tibble(
  x = x_vals
) %>%
  mutate(
    `d1=5, d2=5`   = df(x, df1 = 5, df2 = 5),
    `d1=30, d2=30` = df(x, df1 = 30, df2 = 30),
    `d1=5, d2=30`  = df(x, df1 = 5, df2 = 30),
    `d1=30, d2=5`  = df(x, df1 = 30, df2 = 5)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -x,
    names_to = "parameters",
    values_to = "density"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "d1=5, d2=5",
    "d1=30, d2=30",
    "d1=5, d2=30",
    "d1=30, d2=5"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  "d1=5, d2=5"   = "blue",
  "d1=30, d2=30" = "red",
  "d1=5, d2=30"  = "darkgreen",
  "d1=30, d2=5"  = "purple"
)

# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
  geom_line(linewidth = 1.2) +
  scale_color_manual(values = manual_colors) +
  labs(
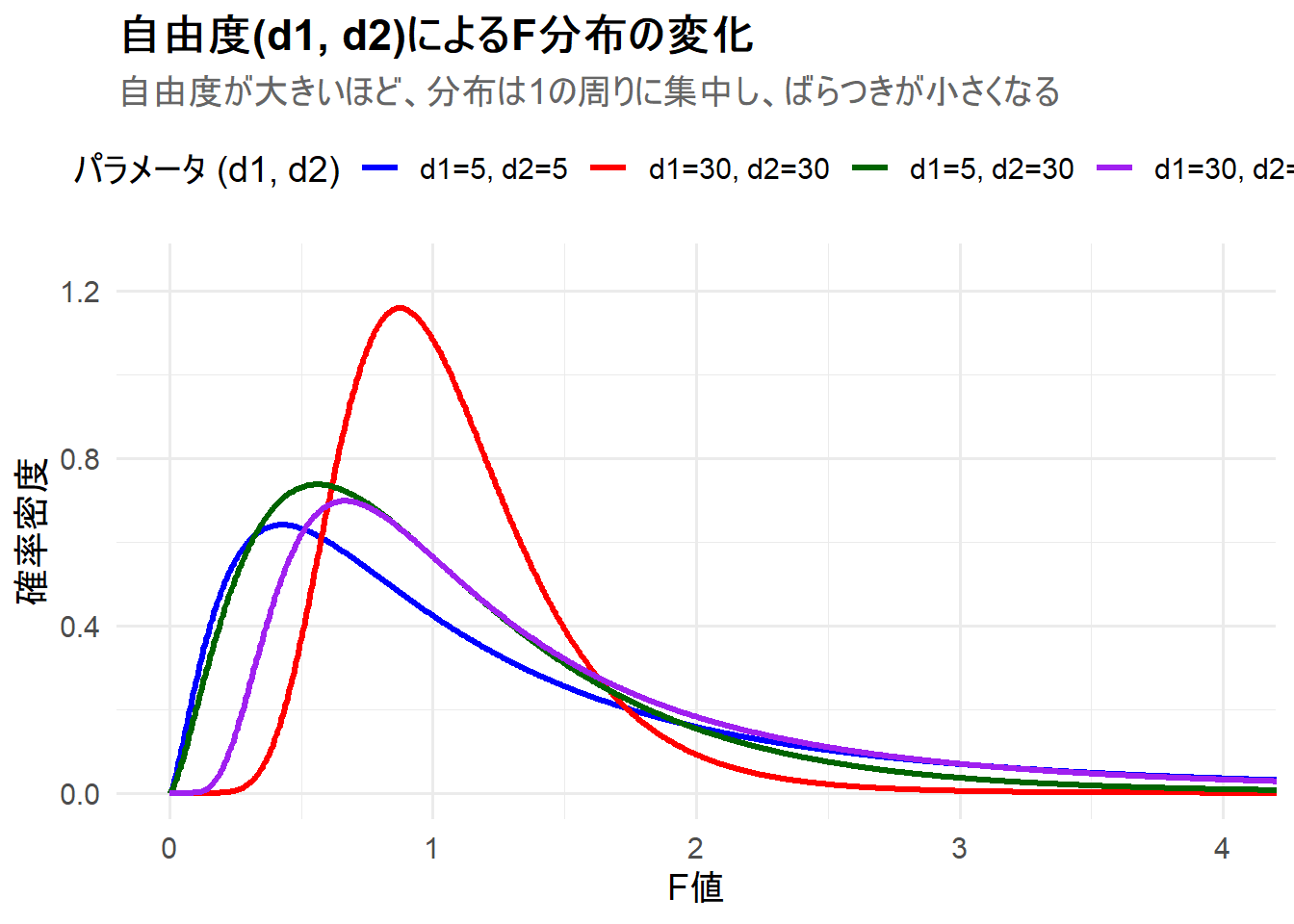
    title = "自由度(d1, d2)によるF分布の変化",
    subtitle = "自由度が大きいほど、分布は1の周りに集中し、ばらつきが小さくなる",
    x = "F値",
    y = "確率密度",
    color = "パラメータ (d1, d2)"
  ) +
  coord_cartesian(xlim = c(0, 4), ylim = c(0, 1.25)) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "top",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40")
  )

# チャートの表示
print(p)

Figure 1 の解説

上記のRコードを実行すると、4つのF分布が描画されたチャート Figure 1 が生成されます。

• d1=5, d2=5 (青線): 分子・分母の自由度が共に小さいため、比較的ばらつきが大きく、右に歪んだ形状をしています。
• d1=30, d2=30 (赤線): 両方の自由度が大きいため、分布のばらつきが最も小さく、ピークは1の近くに集中しています。このチャートの中では最も高く、鋭い山を持つ分布です。
• d1=5, d2=30 (緑線): 分母の自由度d2が大きいため、青線（d1=5, d2=5）と比べて分布のばらつきがやや小さくなり、ピークが高くなっています。ピークの位置は1よりも左にあります。
• d1=30, d2=5 (紫線): 分母の自由度d2が5と小さいため、分布はばらつきが大きく、右に長く裾を引いています。ピークの高さは赤線（d1=30, d2=30）や緑線（d1=5, d2=30）よりも低くなっており、分子の自由度d1が大きいだけではピークが高くなるとは限らないことがわかります。

以上です。