Rで符号検定

目的

符号検定は、以下の2つの主な状況で使われます。

1. 1標本の場合: ある集団の「中央値」が、特定の基準値と等しいかどうかを検定します。
   • 例: 「あるクラスのテストの中央値は50点である」という仮説を検証する。
2. 対応のある2標本の場合: 変化の前後など、ペアになった2つのデータ群の「中央値に差があるか」を検定します。
   • 例: 「新しい薬を投与する前後で、患者の血圧の中央値に変化があったか」を検証する。

検定の考え方

符号検定はその名の通り、差の「符号（プラスかマイナスか）」だけに着目します。差の大きさは一切考慮しません。

対応のある2標本の場合を例に、検定の手順を説明します。

1. 差を計算する: 対応するデータのペア（例: 投与前後の血圧）の差を計算します。
2. 符号を数える: 計算した差がプラス（+）か、マイナス（-）か、ゼロ（0）かを判定します。
3. 仮説を立てる:
   • 帰無仮説 (H₀): 2つのデータ群の中央値に差はない。
     • この仮説が正しければ、差の符号がプラスになる確率とマイナスになる確率は、どちらも 1/2 になるはずです。
   • 対立仮説 (H₁): 2つのデータ群の中央値に差がある。
     • この場合、プラスかマイナスのどちらかに偏るはずです。
4. p値を計算する:
   • 差がゼロのデータは除外します。
   • 残ったデータのうち、プラスの符号の数とマイナスの符号の数を数えます。
   • 「コインを投げて表（プラス）と裏（マイナス）が出る確率が等しい」という状況と同じように、観測された符号の偏りが偶然で起こる確率（p値）を二項分布を用いて計算します。
   • p値が事前に決めた有意水準（例: 0.05）より小さい場合、帰無仮説を棄却し、「中央値に有意な差がある」と結論します。

特徴

• 長所:
  • データの分布が正規分布に従う必要がありません。
  • 計算が非常にシンプルです。
  • 外れ値（極端に大きい、または小さい値）の影響を受けにくい（ロバストである）という強力な利点があります。
• 短所:
  • 差の「大きさ」という情報を無視するため、t検定やウィルコクソンの符号順位検定といった他の手法に比べて、検出力（本当に差があるときに、それを見抜く力）が低い傾向があります。

Step 1: ライブラリの準備

符号検定のためにBSDAパッケージを読み込みます。

# ライブラリの読み込み
library(tidyverse)
library(BSDA)

seed <- 20250705

Step 2: サンプルデータの作成

30人の生徒の学習法導入前 (before) と導入後 (after) のテストの点数データを模擬的に作成します。

ここでは、導入後に多くの生徒の点数が上がったものの、数人は下がったり、変わらなかったりする状況を想定します。また、外れ値（95点を取った優秀な生徒）を1人含めてみます。

# 再現性のための乱数シード設定
set.seed(seed)

# 生徒の人数
n_students <- 30

# 学習法導入前の点数データを作成
# 平均60点、標準偏差10の正規分布に従うとする
before_scores <- round(rnorm(n = n_students, mean = 60, sd = 10))

# 学習法導入後の点数データを作成
# 多くの生徒は点数が上がり(平均+5点)、一部は変わらないか下がる
# 全体にランダムな変動を加える
after_scores <- before_scores + round(rnorm(n = n_students, mean = 5, sd = 4))

# データにいくつかの特徴を加える
after_scores[3] <- before_scores[3] # 1人は点数が変わらない
after_scores[10] <- before_scores[10] - 5 # 1人は点数が下がる
before_scores[5] <- 95 # 外れ値（もともと高得点の生徒）
after_scores[5] <- 98

# 負の点数や100点を超える点数を補正
before_scores <- pmax(0, pmin(100, before_scores))
after_scores <- pmax(0, pmin(100, after_scores))

# データフレームの作成
score_data <- data.frame(
  student_id = 1:n_students,
  before = before_scores,
  after = after_scores
)

cat("--- 作成したデータの一部を確認 ---\n")
head(score_data)

--- 作成したデータの一部を確認 ---
  student_id before after
1          1     48    44
2          2     70    72
3          3     65    65
4          4     73    77
5          5     95    98
6          6     48    53

Step 3: データの可視化

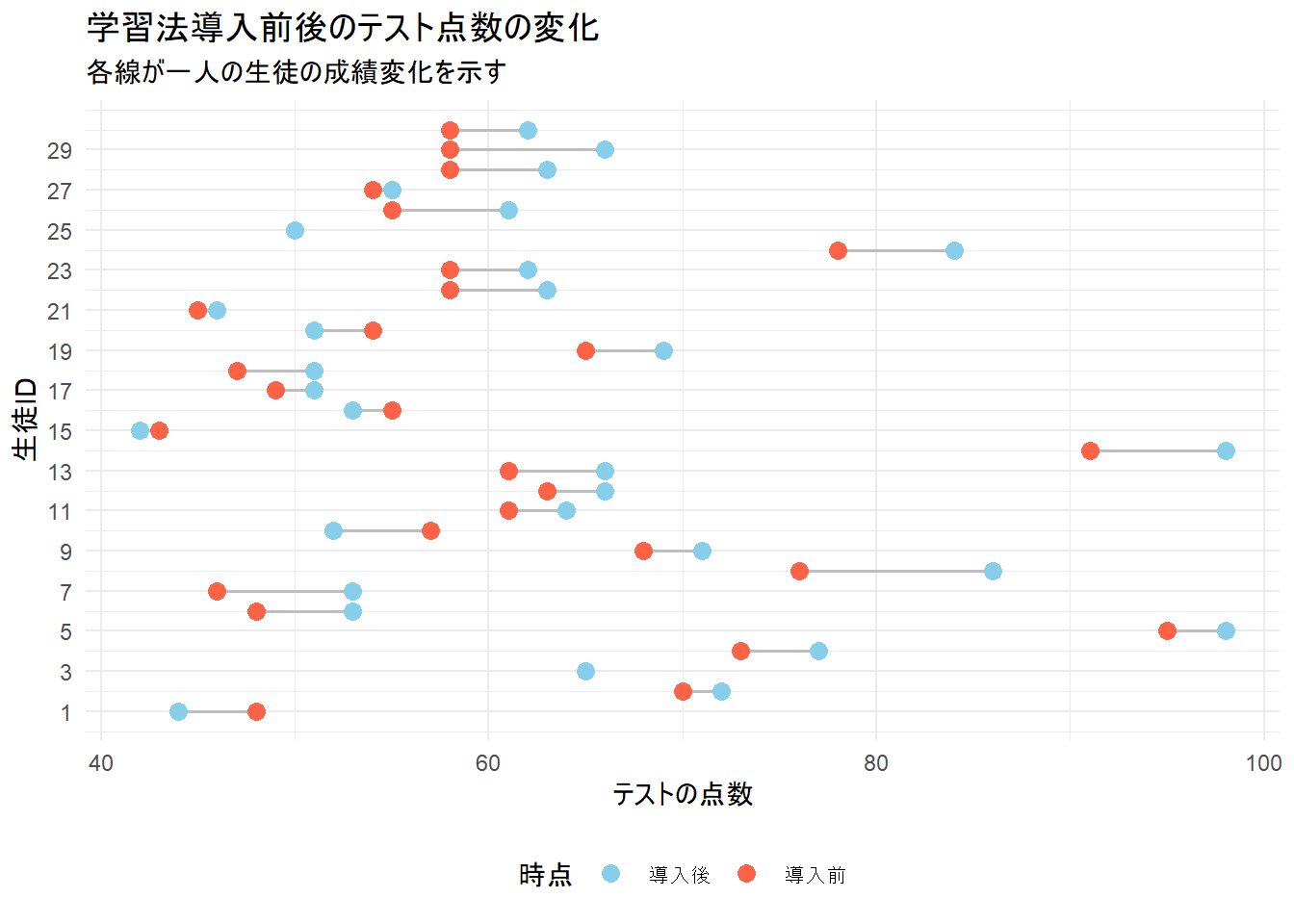
各生徒の点数がどのように変化したかを視覚的に確認します。このような対応のあるデータの可視化には、変化前後の点を線で結んだ「ダンベルプロット」が有効です。

ggplot(score_data, aes(y = student_id)) +
  # 変化前後の点をつなぐ線
  geom_segment(aes(x = before, xend = after, yend = student_id),
    color = "grey",
    linewidth = 0.7
  ) +
  # geom_segment(aes(x = before, xend = after, yend = student_id),
  #              color = "grey",
  #              linewidth = 0.7,arrow = arrow(length = unit(0.3, "cm"))) +
  # 導入前の点
  geom_point(aes(x = before, color = "導入前"), size = 3) +
  # 導入後の点
  geom_point(aes(x = after, color = "導入後"), size = 3) +
  # スケールとラベルの設定
  scale_y_continuous(breaks = seq(1, n_students, by = 2)) + # Y軸の目盛りを調整
  scale_color_manual(
    name = "時点",
    values = c("導入前" = "tomato", "導入後" = "skyblue")
  ) +
  labs(
    title = "学習法導入前後のテスト点数の変化",
    subtitle = "各線が一人の生徒の成績変化を示す",
    x = "テストの点数",
    y = "生徒ID"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")

Figure 1 から、導入前後の各生徒の点数の推移がわかり、多くの生徒が導入前より導入後の方が点数が上昇していることを確認できます(青い点が赤い点より右側にあることが確認できます)。

Step 4: 符号検定のシミュレーション

# 1. 導入前後の差を計算
score_data <- score_data %>%
  mutate(difference = after - before)

# 2. 差の符号を判定
score_data <- score_data %>%
  mutate(sign = sign(difference))

# 3. 符号（+, -, 0）の数を集計
sign_counts <- score_data %>%
  count(sign)

cat("--- 手計算の実行結果 ---\n")
print(sign_counts)

# プラス（点数上昇）とマイナス（点数下降）の数を取得
# 差が0のデータは検定から除外する
n_plus <- score_data %>%
  filter(sign == 1) %>%
  nrow()
n_minus <- score_data %>%
  filter(sign == -1) %>%
  nrow()

cat(paste("点数が上がった生徒（+）:", n_plus, "人\n"))
cat(paste("点数が下がった生徒（-）:", n_minus, "人\n"))

# 4. 二項検定でp値を計算
# 帰無仮説「中央値に差はない（上昇と下降の確率は1/2）」のもとで、
# このような偏りが生じる確率を計算する。
# 全試行回数は、差が0でなかった生徒数
total_trials <- n_plus + n_minus
# 検定統計量は、少ない方の数（今回はマイナス）
test_statistic <- min(n_plus, n_minus)

# 両側検定のp値を計算
# ここは手作業から離れてbinom.testを利用します
b_test_manual <- binom.test(x = test_statistic, n = total_trials, p = 0.5, alternative = "two.sided")
cat("\n--- 二項検定の結果 ---\n")
print(b_test_manual)

--- 手計算の実行結果 ---
  sign  n
1   -1  5
2    0  2
3    1 23
点数が上がった生徒（+）: 23 人
点数が下がった生徒（-）: 5 人

--- 二項検定の結果 ---

    Exact binomial test

data:  test_statistic and total_trials
number of successes = 5, number of trials = 28, p-value = 0.0009122
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.06064291 0.36893335
sample estimates:
probability of success 
             0.1785714 

# SIGN.test() を実行
# 対応のある2標本なので、xとyにそれぞれのデータベクトルを指定する
sign_test_result <- SIGN.test(x = score_data$before, y = score_data$after, alternative = "two.sided")

# 結果の表示
cat("--- SIGN.test()の結果 ---\n")
print(sign_test_result)

--- SIGN.test()の結果 ---

    Dependent-samples Sign-Test

data:  score_data$before and score_data$after
S = 5, p-value = 0.0009122
alternative hypothesis: true median difference is not equal to 0
95 percent confidence interval:
 -4.870878 -2.000000
sample estimates:
median of x-y 
         -3.5 

Achieved and Interpolated Confidence Intervals: 

                  Conf.Level  L.E.pt U.E.pt
Lower Achieved CI     0.9013 -4.0000     -2
Interpolated CI       0.9500 -4.8709     -2
Upper Achieved CI     0.9572 -5.0000     -2

Step 5: 結果の解釈

SIGN.test()の結果を見てみましょう。

• S = 5: 検定統計量。これは差がマイナス（点数が下がった）だった生徒の数に対応しており、手計算の n_minus と一致します。
• p-value = 0.0009122: p値。手計算の二項検定の結果と一致します。
• alternative hypothesis: true median difference is not equal to 0: 対立仮説は「真の中央値の差は0ではない」です。

結論: 得られたp値（0.0009122）は、設定した有意水準である 5% (0.05) よりも小さいです。 したがって、「帰無仮説（学習法の導入前後でテストの点数の中央値に差はない）」を棄却し、「新しい学習法の導入によって、生徒のテストの点数の中央値は有意に変化した」と結論付けることができます。

さらに、median of x-y が -3.5 であることから、点数は増加方向に変化したと解釈できます。

以上です。