Rで 線形代数:ベクトル確率変数の分散共分散行列 を確認します。
1. ベクトル確率変数の分散共分散行列とは
導入:1次元から多次元へ
まず、1つの確率変数 \(X\)(スカラー)を考えます。この変数のばらつきの度合いは分散 (Variance) で表されます。
\[ \text{Var}(X) = E[(X - \mu)^2] \quad (\text{ただし} \mu = E[X]) \]
では、複数の確率変数、例えば身長 (\(X_1\)) と体重 (\(X_2\)) のように、複数の変数を同時に扱いたい場合はどうでしょうか。このとき、それぞれの変数のばらつき(分散)だけでなく、変数同士がどのように関係し合って変動するかも重要になります。この関係性を表すのが共分散 (Covariance) です。
\[ \text{Cov}(X_1, X_2) = E[(X_1 - \mu_1)(X_2 - \mu_2)] \]
- 共分散が正:\(X_1\) が大きいとき、\(X_2\) も大きくなる傾向がある(例:身長と体重)。
- 共分散が負:\(X_1\) が大きいとき、\(X_2\) は小さくなる傾向がある(例:勉強時間と遊ぶ時間。おそらく)。
- 共分散が0に近い:\(X_1\) と \(X_2\) の間に線形な関係はほとんどない。
ベクトル確率変数と分散共分散行列
これらの複数の確率変数をひとまとめにしたものをベクトル確率変数 (Vector Random Variable) と呼びます。\(p\)個の確率変数がある場合、以下のようにベクトルで表現します。
\[ \boldsymbol{X} = \begin{pmatrix} X_1 \\ X_2 \\ \vdots \\ X_p \end{pmatrix} \]
そして、このベクトル確率変数 \(\boldsymbol{X}\) のばらつきと、その要素間の関係性を一つの行列にまとめたものが分散共分散行列 (Variance-Covariance Matrix) です。通常、\(\Sigma\) や \(\text{Var}(\boldsymbol{X})\) と表記されます。
分散共分散行列 \(\Sigma\) は以下のように定義されます。
\[ \Sigma = E \left[ (\boldsymbol{X} - \boldsymbol{\mu})(\boldsymbol{X} - \boldsymbol{\mu})^T \right] \]
ここで、\(\boldsymbol{\mu}\) は各確率変数の期待値(平均)をまとめた期待値ベクトルです。
\[ \boldsymbol{\mu} = E[\boldsymbol{X}] = \begin{pmatrix} E[X_1] \\ E[X_2] \\ \vdots \\ E[X_p] \end{pmatrix} \]
具体的に行列の中身を見てみましょう。\(p=3\) の場合、分散共分散行列は以下のようになります。
\[
\Sigma =
\begin{pmatrix}
\text{Var}(X_1) & \text{Cov}(X_1, X_2) & \text{Cov}(X_1, X_3) \\
\text{Cov}(X_2, X_1) & \text{Var}(X_2) & \text{Cov}(X_2, X_3) \\
\text{Cov}(X_3, X_1) & \text{Cov}(X_3, X_2) & \text{Var}(X_3)
\end{pmatrix}
\]
分散共分散行列の重要な性質
- 対角成分は分散: 行列の対角成分 \((i, i)\) は、確率変数 \(X_i\) の分散です。これは各変数が単独でどれだけばらついているかを示します。
- 非対角成分は共分散: 行列の非対角成分 \((i, j)\) は、確率変数 \(X_i\) と \(X_j\) の共分散です。これは2つの変数がどのように連動するかを示します。
- 対称行列: \(\text{Cov}(X_i, X_j) = \text{Cov}(X_j, X_i)\) であるため、分散共分散行列は常に対角線に対して対称な対称行列になります。
- 半正定値行列: この行列は数学的に半正定値行列という性質を持ちます。これは、任意のベクトル \(\boldsymbol{a}\) に対して \(\boldsymbol{a}^T \Sigma \boldsymbol{a} \ge 0\) となることを意味し、「ばらつき(分散)が負になることはない」ことを保証しています。
分散共分散行列は、多変量正規分布を定義したり、主成分分析(PCA)や因子分析などの多変量解析手法で中心的な役割を果たします。
2. Rによるシミュレーション
ここでは、3次元のベクトル確率変数を考え、理論的な分散共分散行列をまず定義します。次に、その行列をパラメータに持つ多変量正規分布からデータを生成し、そのデータから計算した標本分散共分散行列が、元の理論的な行列に近くなることを確認します。
多変量正規分布からの乱数生成には MASS パッケージの mvrnorm 関数を使うと便利です。
# ----------------------------------------------------
# 1. 準備:ライブラリの読み込み
# ----------------------------------------------------
library(MASS)
# ----------------------------------------------------
# 2. パラメータの設定
# ----------------------------------------------------
# 次元数 (p)
p <- 3
# 生成するサンプルサイズ (n)
# サンプルサイズが大きいほど、標本統計量は理論値に近づきます
n <- 2000
# 理論的な期待値ベクトル (μ)
# X1の平均は0, X2の平均は5, X3の平均は10とする
mu <- c(0, 5, 10)
# 理論的な分散共分散行列 (Σ)
# 対角成分は各変数の「分散」、非対角成分は「共分散」
# Cov(X1, X2) = 2 (正の相関)
# Cov(X1, X3) = -1 (負の相関)
# Cov(X2, X3) = 3 (正の相関)
Sigma <- matrix(c(
4, 2, -1,
2, 5, 3,
-1, 3, 6
), nrow = 3, byrow = TRUE)
# ----------------------------------------------------
# 3. 多変量正規分布に従うデータの生成
# ----------------------------------------------------
# mvrnorm()関数を使い、指定したμとΣを持つデータを生成
seed <- 20250701
set.seed(seed) # 結果を再現可能にするための乱数シード
data <- mvrnorm(n = n, mu = mu, Sigma = Sigma)
# 生成されたデータの最初の数行を確認
cat("--- 生成されたデータの一部を確認 ---\n")
head(data)
# ----------------------------------------------------
# 4. 標本統計量の計算
# ----------------------------------------------------
# 標本平均ベクトルの計算
sample_mu <- colMeans(data)
# 標本分散共分散行列の計算
sample_Sigma <- var(data)
# ----------------------------------------------------
# 5. 結果の比較
# ----------------------------------------------------
cat("\n--- 理論値と標本値の比較 ---\n")
# 期待値ベクトルの比較
cat("\n理論的な期待値ベクトル (μ):\n")
print(mu)
cat("\nデータから計算した標本平均ベクトル:\n")
print(sample_mu)
# 分散共分散行列の比較
cat("\n理論的な分散共分散行列 (Σ):\n")
print(Sigma)
cat("\nデータから計算した標本分散共分散行列:\n")
print(sample_Sigma)
cat("\nサンプルサイズ(n)が大きいため、標本統計量が理論値に近いことがわかります。\n")
# ----------------------------------------------------
# 6. 可視化による関係の確認
# ----------------------------------------------------
# 散布図行列を描画して、変数間の関係を視覚的に確認する
colnames(data) <- c("X1", "X2", "X3")
pairs(data, main = "変数間の関係を示す散布図行列", pch = 19, cex = 0.9)--- 生成されたデータの一部を確認 ---
[,1] [,2] [,3]
[1,] -2.6894983 5.469067 9.232846
[2,] 2.4534713 9.083421 11.065847
[3,] -0.9514335 6.586408 12.224648
[4,] -0.1007101 6.243154 10.246411
[5,] 2.6248618 3.467458 8.441665
[6,] -5.0241032 3.540870 12.273764
--- 理論値と標本値の比較 ---
理論的な期待値ベクトル (μ):
[1] 0 5 10
データから計算した標本平均ベクトル:
[1] -0.0118316 5.0094803 10.0325376
理論的な分散共分散行列 (Σ):
[,1] [,2] [,3]
[1,] 4 2 -1
[2,] 2 5 3
[3,] -1 3 6
データから計算した標本分散共分散行列:
[,1] [,2] [,3]
[1,] 4.1870035 2.173181 -0.9694008
[2,] 2.1731809 4.979039 2.8166094
[3,] -0.9694008 2.816609 5.8000183
サンプルサイズ(n)が大きいため、標本統計量が理論値に近いことがわかります。シミュレーション結果の解説
- パラメータの設定: まず、3つの確率変数 (\(X_1, X_2, X_3\)) の関係性を定義する「理論的な分散共分散行列
Sigma」を準備しました。-
Sigma[1, 2]は2なので、\(X_1\) と \(X_2\) には正の相関があります。 -
Sigma[1, 3]は-1なので、\(X_1\) と \(X_3\) には負の相関があります。 -
Sigma[2, 3]は3なので、\(X_2\) と \(X_3\) には強い正の相関があります。
-
- データ生成と計算: この
Sigmaをもとに、mvrnormで2000個のデータを生成しました。そして、生成されたデータからcolMeans()で標本平均を、var()で標本分散共分散行列を計算しました。 - 結果の比較: 出力を見ると、標本平均ベクトル (
sample_mu) は理論値muに、標本分散共分散行列 (sample_Sigma) は理論値Sigmaに近い値になっていることが確認できます。 - 可視化: 最後に
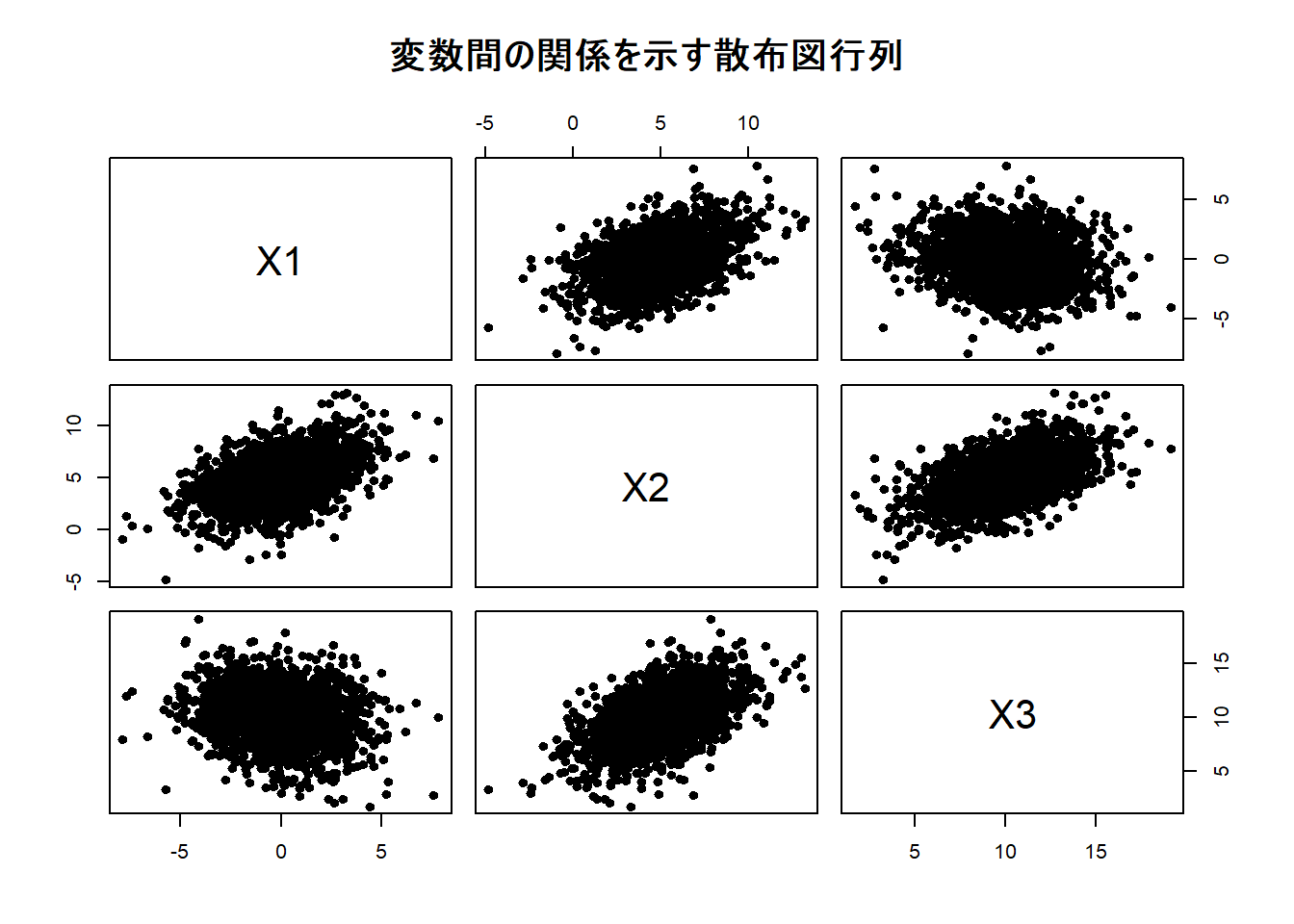
pairs()で描画した散布図行列を見ると、設定した変数間の関係が視覚的に分かります。- \(X_1\) と \(X_2\) のプロットは右肩上がりの傾向が見られ、正の相関があることがわかります。
- \(X_1\) と \(X_3\) のプロットは右肩下がりの傾向が見られ、負の相関があることがわかります。
- \(X_2\) と \(X_3\) のプロットは明確な右肩上がりの傾向があり、強い正の相関が確認できます。
このように、分散共分散行列により多次元データのばらつきと変数間の相関構造をコンパクトに表現することができます。
以上です。